神经网络和深度学习-多分类问题Softmax Classifier
多分类问题Softmax Classifier
在之前做糖尿病数据集的时候做的二分类问题,因为只有两类,所以只需要输出一个概率值,另一个概率值用1去减去就可以得到
实际上在大多数数据集中是在处理一个多分类问题,例如MNIST中有10类标签
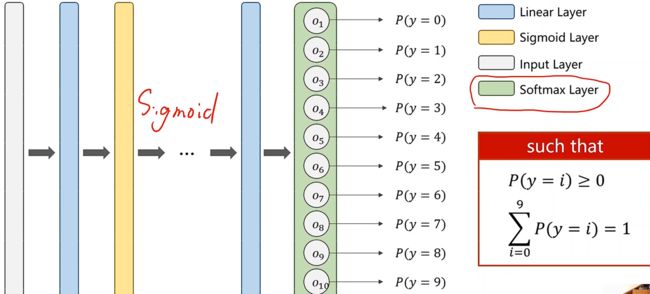
神经网络如何设计
我们在输出的时候,在原来只有p(y=1)的输出变为10个输出,这样就可以输出每一个样本属于每一个分类的概率,可能出现大多数分类都是高概率,这其中肯定是矛盾的,希望在输出的分类的概率需要满足一个分布的要求,满足离散分类
-
全部概率>0
-
总概率 = 1
Softmax Layer
在处理多分类问题的时候,在前面的神经网络还是采用Sigmoid Layer,在最终输出层中我们使用Softmax Layer
下面我们就要针对分布要求,看看Softmax Layer是如何设计的
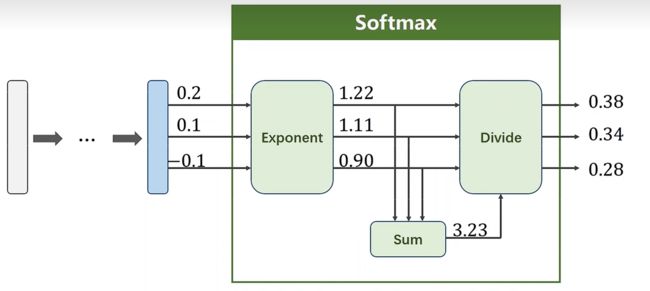
P ( y = i ) = e z i ∑ j = 0 K − 1 e z j , i ∈ { 0 , … , K − 1 } P(y=i)=\frac{e^{z_{i}}}{\sum_{j=0}^{K-1} e^{z_{j}}}, i \in\{0, \ldots, K-1\} P(y=i)=∑j=0K−1ezjezi,i∈{0,…,K−1}
-
在分子部分,我们可以满足全部概率>0
-
在分母部分,满足总概率 = 1
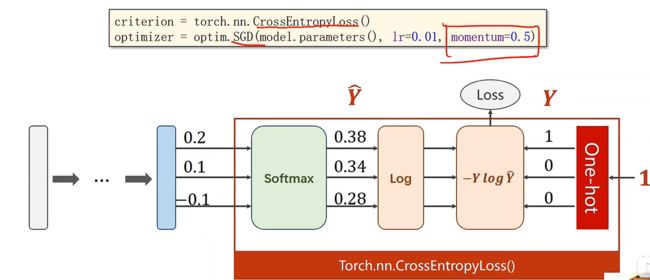
假设我们有三个分类,经过线性之后我们有了三个输出值(0.2,0.1,-0.1),之后经过exp、sum、divide这三步,最终得到这三个类的概率y hat
Loss function
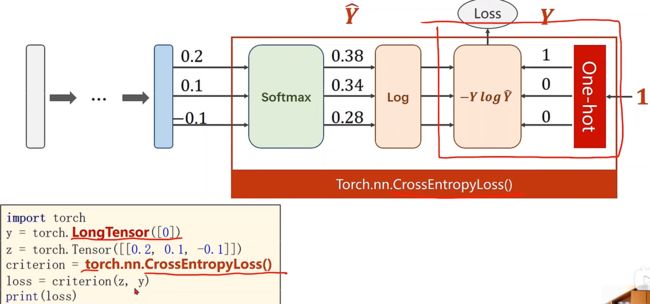
我们使用one-hot独热编码来解决多分类这个问题,只会保存Y=1的项
Loss ( Y ^ , Y ) = − Y log Y ^ \operatorname{Loss}(\hat{Y}, Y)=-Y \log \hat{Y} Loss(Y^,Y)=−YlogY^
在torch中有这么一个损失,NLLLoss(Negative Log Likelihood Loss),这个函数的功能是:Y输入的就是标签号
在Numpy中的Cross Entropy
在PyTorch中的Cross Entropy,提供了交叉熵损失这个函数
我们来看一个具体的例子,加入有三个样本,分别属于(2,0,1)类
第一个预测中Y_pred1对应得分类都比较准确,所以损失会小
第二个预测中Y_pred2对应得分类都不准确,所以损失会比较大
交叉熵损失和NLL损失之间的关系
MNIST Dataset
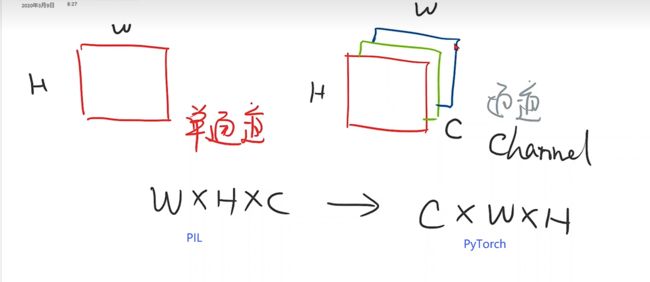
在数据集中一个图像是28*28=784个像素点组成的,每一个像素点的取值是0-255。
做一个线性映射到0-1的区间,我们可以看到在矩阵中就表示了图的形状
多分类实现MNIST Dataset
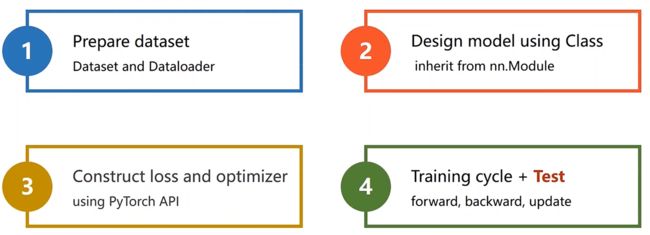
按照四个步骤,最后要加上测试集
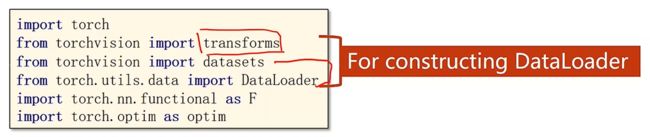
工具包部分
其中用到的transforms针对图像进行一些处理,还用到了relu激活函数所需要用到torch.nn.functional
Prepare Dataset
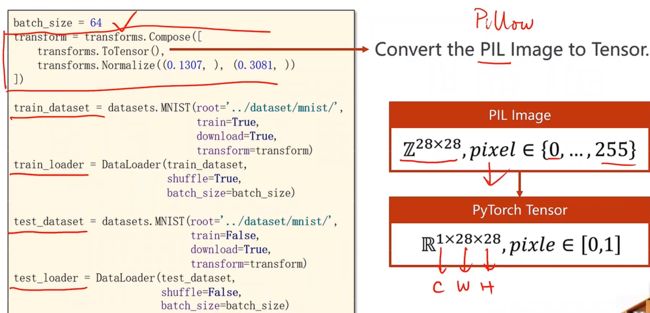
用transform把原始PIL的图像转换为Tensor的图像格式
这个过程就可以用transforms中的ToTensor来实现
其中Normalize中第一个(0.1307,)就是求mean,第二个(0.3081,)就是std标准化,这两个值是在计算了整个数据集的mean和std得到的结果,所用到的归一化方程如下
P i x e l norm = Pixel origin − mean std Pixel _{\text {norm }}=\frac{\text { Pixel }_{\text {origin }}-\text { mean }}{\text { std }} Pixelnorm = std Pixel origin − mean
Design Model
输入图像为(N,1,28,28)其中有N个样本。
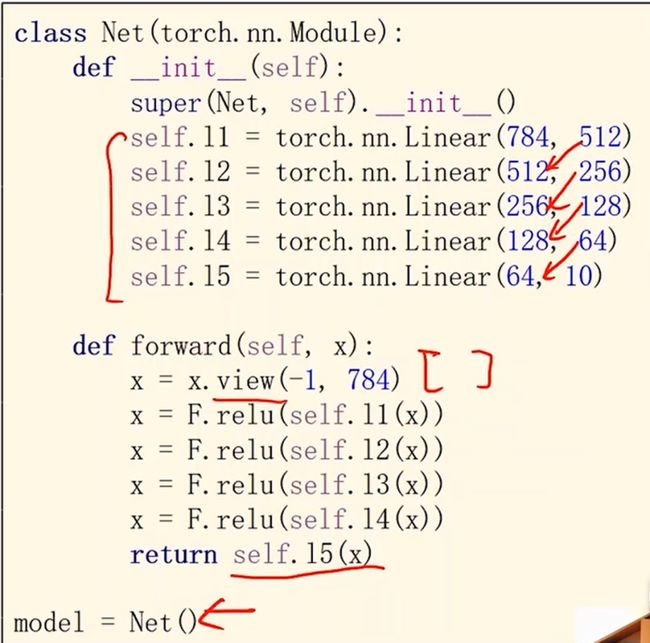
第一步就是把(1,28,28)这个三阶张量变成向量,用view函数来改变张量的形状(-1,784)二阶张量,第一个值是-1代表自动去算它的值是多少,比如N为64,则把-1 变为64,第二个值是图像的像素点,最后我们拿到的是N*784的矩阵,经过一系列的层,输出层得到(N,10),10个类
我们来看一下代码
Construct Loss and Optimizer
在criterion中我们使用交叉熵损失CrossEntropyLoss
在optimizer中我们使用更好的优化方法,带有冲量momentum(相当于是赋予梯度惯性,让它尽可能跳出局部最低点),设置为0.5来优化训练过程
Train and Test
将epoch封装在train函数中,输出300次迭代输出一次损失
优化器在优化之前就选择清零
在test函数中,我们只需要计算前向传播
我们在做完预测得到输出矩阵,每个样本都有一行,一行有10个量,我们要求最大值的下标是多少,使用torch.max,dim=1指的是行数,反之为0,指列数。返回的值是两个,每一行的最大值和每一行最大值的下标
最后可以计算准确率=正确数/总数
在训练的过程中只需要调用函数即可,也可以每十轮输出一次测试
在输出中我们可以看到loss在减少,accuracy在上升,但可能会存在极限
完整代码
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# prepare dataset
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 归一化,均值和方差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(784, 512)
self.l2 = torch.nn.Linear(512, 256)
self.l3 = torch.nn.Linear(256, 128)
self.l4 = torch.nn.Linear(128, 64)
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x):
x = x.view(-1, 784) # -1其实就是自动获取mini_batch
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) # 最后一层不做激活,不进行非线性变换
model = Net()
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
# 获得一个批次的数据和标签
inputs, target = data
optimizer.zero_grad()
# 获得模型预测结果(64, 10)
outputs = model(inputs)
# 交叉熵代价函数outputs(64,10),target(64)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:
print('[%d,%5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1) # dim = 1 列是第0个维度,行是第1个维度
total += labels.size(0)
correct += (predicted == labels).sum().item() # 张量之间的比较运算
print('accuracy on test set: %d %% ' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
运行结果:
[1, 300] loss: 2.161
[1, 600] loss: 0.838
[1, 900] loss: 0.429
accuracy on test set: 89 %
[2, 300] loss: 0.329
[2, 600] loss: 0.269
[2, 900] loss: 0.237
accuracy on test set: 93 %
[3, 300] loss: 0.192
[3, 600] loss: 0.179
[3, 900] loss: 0.157
accuracy on test set: 95 %
[4, 300] loss: 0.139
[4, 600] loss: 0.126
[4, 900] loss: 0.119
accuracy on test set: 96 %
[5, 300] loss: 0.096
[5, 600] loss: 0.098
[5, 900] loss: 0.101
accuracy on test set: 96 %
[6, 300] loss: 0.080
[6, 600] loss: 0.077
[6, 900] loss: 0.078
accuracy on test set: 97 %
[7, 300] loss: 0.063
[7, 600] loss: 0.064
[7, 900] loss: 0.064
accuracy on test set: 97 %
[8, 300] loss: 0.051
[8, 600] loss: 0.058
[8, 900] loss: 0.048
accuracy on test set: 97 %
[9, 300] loss: 0.041
[9, 600] loss: 0.044
[9, 900] loss: 0.045
accuracy on test set: 97 %
[10, 300] loss: 0.033
[10, 600] loss: 0.036
[10, 900] loss: 0.036
accuracy on test set: 97 %