【论文阅读】ICRA2021: VDB-EDT An Efficient Euclidean Distance Transform Algorithm Based on VDB Data Struct
参考与前言
Summary: 浩哥推荐的一篇 无人机下的建图 and planning实验
Type: ICRA
Year: 2021
论文链接:https://arxiv.org/abs/2105.04419
youtube presentation video:https://youtu.be/Bojh6ylYUOo
代码链接:https://github.com/zhudelong/VDB-EDT
1. Motivation
Eucliden distance transform EDT 对于机器人运动规划是很重要的,但是生成EDT 是比较费时的一件事,同时需要时刻更新并维护这样一个地图,本篇文章主要 通过优化数据结构和distance transform的过程来提升EDT算法的速度
在本文中,我们采用了树结构进行 hashing-based EDTs,主要是在做规划时发现 最优轨迹其实值需要考虑一定范围的障碍物, full distance information其实对于规划来说是冗余的,所以实际free部分都是一个值。These regions can then be efficiently encoded by a few number of tree nodes. Such a property is called spatial coherency, which can help further reduce memory consumption.
Benefiting from the fast index and caching systems, VDB achieves a much faster random access speed than Octree and also exhibits a competitive performance with the voxel hashing.
Contribution
- the first time introduce the VDB data structure for distance field representation, which significantly reduces the memory consumption of EDT.
- we propose a novel algorithm to facilitate distance transform procedure and significantly improve the running speed of conventional EDT algorithms.
2. Method
首先是问题定义,一个典型的distance transform问题 可以表达为如下公式:
d ( x i ) = min x j f ( x i , x j ) , s.t. x i ∈ M f , x j ∈ M o \begin{array}{ll}d\left(x_i\right)=\min _{x_j} f\left(x_i, x_j\right), \\\text { s.t. } \quad x_i \in \mathcal{M}_f, x_j \in \mathcal{M}_o\end{array} d(xi)=minxjf(xi,xj), s.t. xi∈Mf,xj∈Mo
其中,Mf是指free space,Mo是被占据空间,x为在grid map M中的坐标,目标函数f表示xi到xj之间的距离,目标是搜索对于每个xi都找其最近的xj作为距离
随后问题有了d(x) 后 我们就走到了 要找到一条安全的路径,则问题可表述为如下:
min x 0 : N ∑ i = 0 N α ∥ x i + 1 − x i ∥ + ( 1 − α ) max ( 0 , d max − d ( x i ) ) s.t. x i , x i + 1 ∈ M f x 0 = x s , x N = x f g ( x i , x i − 1 , x i + 1 ) < θ \begin{array}{ll}\min _{x_{0: N}} & \sum_{i=0}^N \alpha\left\|x_{i+1}-x_i\right\|+(1-\alpha) \max \left(0, d_{\max }-d\left(x_i\right)\right) \\\text { s.t. } & x_i, x_{i+1} \in \mathcal{M}_f \\& x_0=x_s, x_N=x_f \\& g\left(x_i, x_{i-1}, x_{i+1}\right)<\theta\end{array} minx0:N s.t. ∑i=0Nα∥xi+1−xi∥+(1−α)max(0,dmax−d(xi))xi,xi+1∈Mfx0=xs,xN=xfg(xi,xi−1,xi+1)<θ
其中,dmax是最大的transform distance,xs起点,xf终点,alpha为balance coefficient,g 主要是介绍了VDB结构,由Museth[25] 提出的。It sufficiently exploits the sparsity of volumetric data, and employs a variant of B+ tree [32] to represent the data hierarchically. 下图是1D结构下的VDB,其和B+的几个特性是一致的,root node为索引,由hashmap建立,下面为internal node 和 leaf node保存了数据。也有本质上的不同: it encodes values in internal nodes, called tile value. The tile value and child pointer exclusively use the same memory unit, and a flag is additionally leveraged to identify the different cases. A tile value only takes up tens of bits memory but can represent a large area in the distance field, which is the key feature leveraged to improve memory efficiency. B+是一种平衡tree,在数据库中常用,主要原因是对于树结构的查询,程序加载子节点都需要进行一次磁盘IO,磁盘IO 比 读内存IO要慢 所以多叉的B+ tree可以减少I/O的次数 感觉这个看文中会比较好 主要是针对伪代码的解释 The distance field represented by VDB is essentially a sparse volumetric grid, and each field point is represented by a grid cell s indexed by a 3-D coordinate. 更新部分code: 各个阈值对时间的影响,其中对比了几个baseline方法如下: 可以看到 在时间上-Ex 的耗时都比无Ex的快,虽然VDB的速度上比arr的还是慢了一点 10%-25%,但是从memeory cost上确实节约了30-60%的 Herein, the increment of time cost is inevitable, as VDB is based on tree structures and has a slower random access speed than the array-based implementation 同样表格是在数据集上的表现,在global 和 incremental transform会慢一点,但是在memory上省了不少 还有一个就是无人机在仿真环境中建图并有planning效果: 提出了一种VDB-EDT算法去解决 distance transform problem. The algorithm is implemented based on a memory-efficient data structure and a novel distance transform procedure, which significantly improves the memory and runtime efficiency of EDTs. 这项工作突破了通常的EDT的限制,也可以为后面基于VDB-based mapping, distance transform and safe motion planning的研究进行使用 赠人点赞 手有余香 ;正向回馈 才能更好开放记录 hhh2.1 数据结构
参考:b站视频 “索引”的原理 4min 建议感兴趣的可以再查询进阶数据结构书籍了解 实际上代码是直接openvdb库直接构建的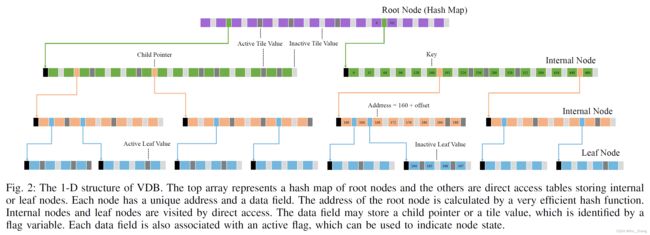
2.2 VDB-EDT
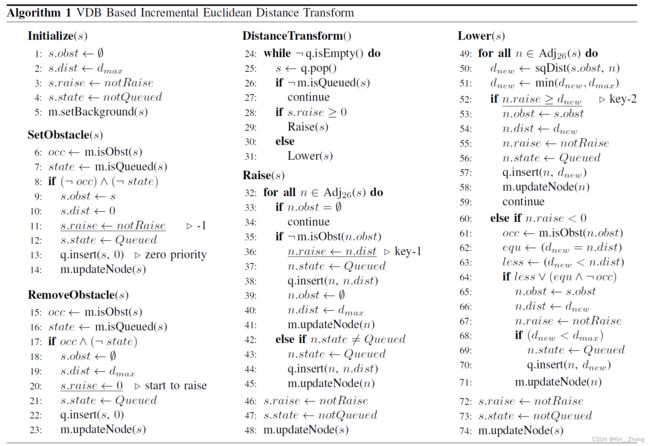

void VDBMap::update_occmap(FloatGrid::Ptr grid_map, const tf::Vector3 &origin, XYZCloud::Ptr xyz)
{
auto grid_acc = grid_map->getAccessor();
auto tfm = grid_map->transform();
openvdb::Vec3d origin3d(origin.x(), origin.y(), origin.z());
openvdb::Vec3d origin_ijk = grid_map->worldToIndex(origin3d);
for (auto point = xyz->begin(); point != xyz->end(); ++point) {
openvdb::Vec3d p_xyz(point->x, point->y, point->z);
openvdb::Vec3d p_ijk = grid_map->worldToIndex(p_xyz);
openvdb::Vec3d dir(p_ijk - origin_ijk);
double range = dir.length();
dir.normalize();
// Note: real sensor range should stractly larger than sensor_range
bool truncated = false;
openvdb::math::Ray<double> ray(origin_ijk, dir);
// openvdb::math::DDA3. 实验及结果
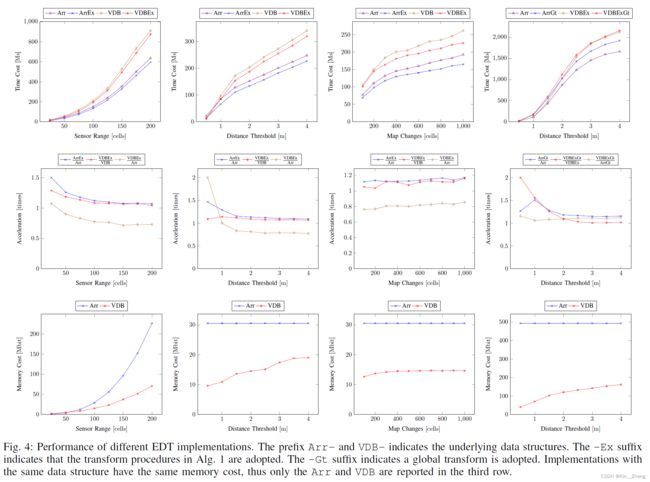
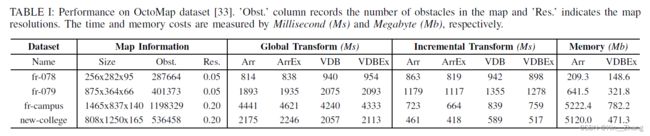
4. Conclusion