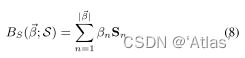SMPL-论文解读
文章目录
- 创新点
- 算法
-
- shape blend shape:
- pose blend shape
- Joint location
- SMPL model
- 训练过程
-
- Pose Parameter Training
- joint regressor
- Shape Parameter Training
- Optimization summary
- DMPL
- 实验
- 结论
论文: 《SMPL: A skinned multi-person linear model》
github: https://smpl.is.tue.mpg.de/
创新点
作者提出一个可学习模型SMPL,其可准确表示各种体型、各种自然姿势下的人体。
LBS、DQBS在膝盖、肘部、肩膀和臀部产生严重的伪影,如图2;

算法
SMPL解耦body shape为identity-dependent shape和non-rigid pose-dependent shape;创建mesh包括N=6890个顶点、K=23个关键点;
在无姿态 θ ⃗ ∗ \vec\theta^* θ∗下平均模板shape T ‾ ∈ R 3 N \overline T \in R^{3N} T∈R3N,blend weight, w ∈ R N × K w \in R^{N \times K} w∈RN×K,如图3a所示;
依靠身材的blend shape函数 B s ( β ⃗ ) : R ∣ β ⃗ ∣ → R 3 N B_s(\vec \beta):R^{|\vec \beta|} \rightarrow R^{3N} Bs(β):R∣β∣→R3N,其中 β ⃗ \vec\beta β为输入形状参数向量,输出a blend shape sculpting the subject identity;
预测K个关键点函数 J ( β ⃗ ) : ( β ⃗ ) : R ∣ β ⃗ ∣ → R 3 K J(\vec \beta):(\vec \beta):R^{|\vec \beta|} \rightarrow R^{3K} J(β):(β):R∣β∣→R3K,如图3b;
依靠姿态的blend shape函数 B p ( θ ⃗ ) : R ∣ θ ⃗ ∣ → R 3 N B_p(\vec \theta):R^{|\vec \theta|} \rightarrow R^{3N} Bp(θ):R∣θ∣→R3N,输入姿态参数 θ ⃗ \vec\theta θ,该模块解释姿势变形的影响,如图3c所示;
最后标准蒙皮函数 W ( . ) W(.) W(.)将blend weight w w w应用于 J ( β ⃗ ) J(\vec \beta) J(β)估计的关键点周围顶点进行旋转变化,如图3d;
SMPL模型 M ( β ⃗ , θ ⃗ ; Φ ) : R ∣ θ ⃗ ∣ × ∣ β ⃗ ∣ → R 3 N M(\vec \beta,\vec \theta;\Phi):R^{|\vec \theta|\times|\vec \beta|}\rightarrow R^{3N} M(β,θ;Φ):R∣θ∣×∣β∣→R3N如式5、顶点可经过式7进行变形;
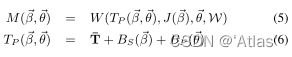

shape blend shape:
如式8, β ⃗ \vec \beta β为输入形状参数; S S S为可学习参数;输出a blend shape sculpting the subject identity;
pose blend shape
Joint location
J J J为变换顶点到关键点的矩阵;其建模哪些顶点重要及如何将它们与关键点位置结合,如式10;
![]()
SMPL model
SMPL模型可学习参数定义为 Φ = { T ‾ , w , S , J , P } \Phi=\{\overline T,w,S,J,P\} Φ={T,w,S,J,P},通过 β ⃗ \vec\beta β、 θ ⃗ \vec\theta θ控制人体身材及姿态变化;SMPL模型 M ( β ⃗ , θ ⃗ ; Φ ) M(\vec\beta,\vec\theta;\Phi) M(β,θ;Φ)定义如式11,
![]()
mesh上每个顶点变换如式12,
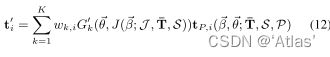
其中 t P , i ( β ⃗ , θ ⃗ ; T ‾ , S , P ) t_{P,i}(\vec\beta,\vec\theta;\overline T,S,P) tP,i(β,θ;T,S,P)=

表示应用于blend shape后的顶点 i i i;
训练过程
首先在多姿态数据集训练参数 { J , w , P } \{J,w,P\} {J,w,P},在多体态数据集训练参数 { T ‾ , S } \{\overline T,S\} {T,S}
Pose Parameter Training
E D E_D ED使用平方损失函数,计算registration(表示mesh对齐)顶点与模型顶点距离, s ( j ) s(j) s(j)为与registration j对应的目标人体index

E Y E_Y EY用于惩罚左右不对称;
![]()
E J E_J EJ计算回归器 J I J_I JI预测关键点到真实关键点距离;

E P E_P EP防止姿态blend shape过拟合,对它们正则化到0;
![]()
E w E_w Ew正则化blend weight到初始化权重,如图6所示;
![]()

训练 { W , P } \{W,P\} {W,P}的总损失函数如公式14;
![]()
joint regressor
关键点回归器 J J J使用非负最小二乘损失,包含正则项,使得使用稀疏顶点预测关键点位置,如图7所示;

Shape Parameter Training
姿态归一化将原始对齐mesh, V j S V^S_j VjS转换到无姿态下对齐mesh, T ^ j S \hat T^S_j T^jS;归一化使得姿态和体态可分开建模;
最小化变换后模型的边与真值边(相邻顶点的差)之间差值, θ ⃗ j = \vec \theta_j= θj=
![]()
θ ⃗ \vec \theta θ确定后,确定 T j S T^S_j TjS,如下式,
![]()
对 { T ^ j S } \{\hat T^S_j\} {T^jS} j = 1 S s u b j ^{S_{subj}}_{j=1} j=1Ssubj进行PCA获得 { T ‾ , S } \{\overline T,S\} {T,S};
Optimization summary
1、式14中姿态参数 θ ⃗ j \vec \theta_j θj首先初始化,通过式15最小化模型边与对齐mesh边之间差异;
2、如式14,进行估计 { T ^ P , J ^ P , w , P , Φ } \{\hat T^P, \hat J^P,w, P,\Phi\} {T^P,J^P,w,P,Φ};
3、进行回归器J的估计;
4、对姿态归一化目标进行PCA降维获得 { T ‾ , S } \{\overline T,S\} {T,S};
DMPL
因为目标间体型差异大,为了抓住这个信息,DMPL增加动态项,如式16,17
![]()
![]()
实验
结论
我们的目标是创建骨骼驱动人体模型,可以捕获身体形状和姿态变化,与现有的图形计算和软件兼容;训练模型最小化顶点重构误差,包括the rest template, joint regressor, body shape model, pose blend shapes, and dynamic blend shapes;