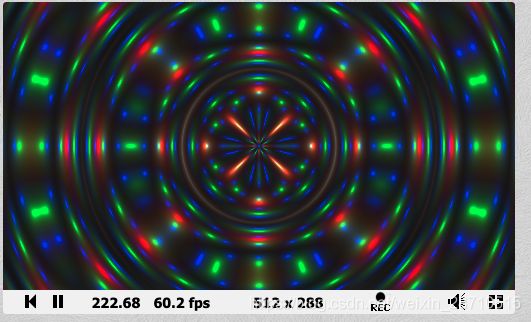
TheBookOfShders学习教程(1)
本文是学习了 The Book of Shaders 的算法绘图章节所做的一个例子,参考了 Danguafer的作品,本文侧重分析和理解,这也是学习Shader的难点!
以下代码都是在ShaderToy网站上测试运行,只要将代码拷贝粘贴到代码窗口,即可运行,希望阅读本文之前,你有一定的ShaderToy经验,可以参考我以前写过的一系列初级教程。
本案例最终效果看这里
下面一步步来完成:
先看一个简单的以距离作为为颜色的例子,代码的注释在代码中。
#define t iTime
#define r iResolution.xy
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
float l;
// 把像素坐标规范化为[0,1]的uv坐标
vec2 uv, p = fragCoord/r;
// 把坐标范围从[0,1]变为[-.5, .5], 这样原点在屏幕中央。
p-=.5;
// p的x坐标考虑屏幕宽高比
p.x *= r.x/r.y;
// 距离场:p到原点的距离。距离作为颜色返回
l = length(p);
if (l>1.) fragColor = vec4(0.,1.,0.,1.);
else fragColor = vec4(vec3(l),t);
}
效果如下,可以看出4个角处有距离大于1的情况,不过毕竟是非常小部分,几乎可以忽略。

所以代码可以简化为
#define t iTime
#define r iResolution.xy
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
float l;
// 把坐标规范化为[0,1]
vec2 uv, p = fragCoord/r;
// 把坐标范围变为[-.5, .5]
p-=.5;
// p的x坐标考虑屏幕宽高比
p.x *= r.x/r.y;
// 距离场:p到原点的距离。距离作为颜色返回
l = length(p);
fragColor = vec4(vec3(l),t);
}
理解一下:上面例子中,颜色实际上是像素点坐标的长度的函数。
现在我们要增加复杂性,ShaderToy是应用算法或者数学函数来绘制各种形状和效果。修改以上代码:
- 增加一个vec3表示颜色,
vec3 c,用来存储屏幕像素坐标到颜色的映射; - 将
uv=p,保持uv坐标; - 将fragColor改为:
fragColor = vec4(c, t), - 将c的赋值改为一个循环来完成
- 循环体内颜色分量的赋值:
c[i] =0.05/length(abs(mod(uv,1.)-.5));.
代码如下:
#define t iTime
#define r iResolution.xy
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec3 c;
float l;
// 把坐标规范化为[0,1]
vec2 uv, p = fragCoord/r;
uv=p;
// 把坐标范围变为[-.5, .5]
p-=.5;
// p的x坐标考虑屏幕宽高比
p.x *= r.x/r.y;
// 距离场:p到原点的距离。距离作为颜色返回
l = length(p);
// 采用一个循环为颜色赋值
for(int i=0;i<3;i++) {
c[i] =0.05/length(abs(mod(uv,1.)-.5));
}
fragColor = vec4(c,t);
}
首先分析一下这个函数:c = .05/length(abs(mod(uv,1.)-.5))
uv坐标对1.取模,结果还是一个vec2,再减去.5,原来的取值范围从0~1变为-.5~.5,然后再取abs绝对值,变为正数,比如vec2(-.2,0.5)通过abs后变为(.2,.5),然后向量求长度,再用0.05来除以它。
uv是一个vec2类型的坐标,mod(uv,1.)返回也是一个vec2类型的坐标。mod(uv,1.)-.5写法跟这两种写法等价:mod(uv,1.)-vec2(.5)或者mod(uv,1.)-vec2(.5,.5),
如果uv的x,y值取值范围都在0~1之间,其实上述写法跟 uv-0.5没啥不同。但是这里我们还是写上mod(uv,1.),因为后续uv的取值范围不限于0~1之间。
同时,mod(x,y)在y取值为1时,同fract等价,用户可以把:mod(uv,1.)-.5改成fract(uv)-.5试试。
这里有个问题,我们怎么知道大致画出来的图形是什么样子?这就是为什么造型函数很重要!
由于uv有x,y两个分量,我们一般的工具不能使用两个自变量来模拟,所以我们把它拆成两个函数f1(x), f2(x)来表达,最终的输出用f3(x)来表示:
f1(x) = abs(mod(x,1.)-.5) //代表y分量
f2(x) = abs(mod(x,1.)-.5) //代表x分量
f3(x) = .05/sqrt(f1(x)* f1(x)+f2(x)* f2(x)) //length使用sqrt来表达。
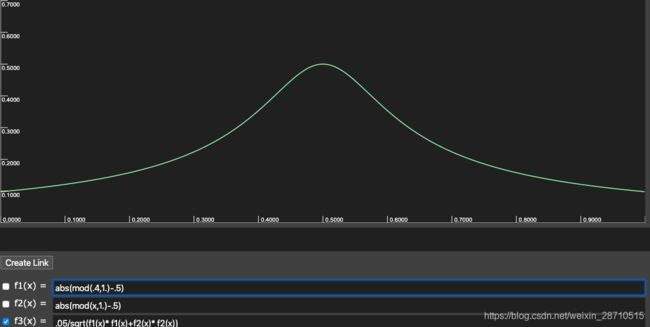
这里要用到一个在线工具GraphToy,在GraphToy中绘制出来f3(x)是这样一个曲线:

目前uv的x,y值取值范围都在0~1之间,曲线为:

无论是x方向,还是y方向,可以推测中间为白色值
可以看出无论你的uv如何变化,它都是一个不断重复变化的曲线,这一点很重要!
上述函数隐含了一个条件,就是x取值都是一个,上述f3(x)曲线是在x方向,y方向取相同的值等到的,为了固定y值,看曲线如何随x变化而变化,可以把代表y分量的函数分别取值0,0.5,0.9再观察f3(x)曲线的变化,如下图所示,

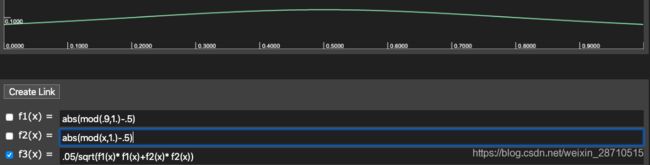
根据对称性,可以推测中央是一个白色的椭圆,颜色(1.1.,1.)。如下图所示:

至此,我们显示效果依旧很呆板,仅仅显示了一个灰不溜秋的椭圆,
理解一下:颜色依旧是像素的函数,再下面的修改中,我们会看到,颜色是时间的函数,屏幕中某个像素点的颜色随着时间而变化,从而使屏幕颜色鲜活起来。这一点很重要!
现在我们把uv的求值也变成一个函数。
其中,uv+=p/l*(sin(z)+1.)*abs(sin(l*9.-z*2.))的曲线如下:
函数右边可以变为:uv+=p/length(p)*(sin(z)+1.)*abs(sin(length(p)*9.-z*2.))
进一步:
uv.x+=p.x/length(p)*(sin(z)+1.)*abs(sin(length(p)*9.-z*2.))
uv.y+=p.y/length(p)*(sin(z)+1.)*abs(sin(length(p)*9.-z*2.))
这个函数有两个自变量,一个是z时间,一个是像素坐标。
要模拟这个函数就有点难度了,坐标的变化已经成了随时间变化而变化了。
为简单起见,设定一个像素点坐标,来看函数的变化趋势,假设p点为(0.5, 0.3),随时间变化,uv坐标变化曲线,注意,这里的x是时间。
f1(x) = 0.5+0.5/sqrt(.5*.5+.3*.3)(sin(x)+1.)abs(sin(sqrt(.5.5+.3.3)9.-x2.))
f2(x) = 0.3+0.3/sqrt(.5*.5+.3*.3)(sin(x)+1.)abs(sin(sqrt(.5.5+.3.3)9.-x2.))

最终,屏幕上某点坐标映射的颜色随时间波动的曲线如下图:
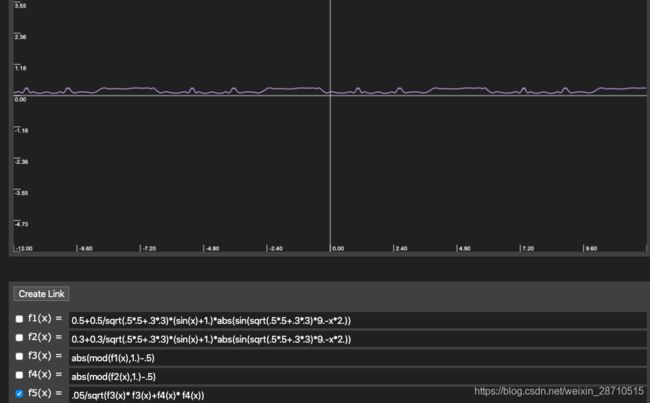
可以看出无论时间怎么变化,曲线总是周期性的变化。
如果坐标点变为(0.1, 0.3),曲线会成这样,但是无论怎么变函数曲线的特征不变,随时间周期性波动。
 理解一下:现在屏幕上每个像素点的颜色随着时间周期性变化。
理解一下:现在屏幕上每个像素点的颜色随着时间周期性变化。
最终代码如下:
#define t iTime
#define r iResolution.xy
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec3 c;
float l,z=t;
// 把坐标规范化为[0,1]
vec2 uv, p = fragCoord/r;
uv=p;
// 把坐标范围变为[-.5, .5]
p-=.5;
// p的x坐标考虑屏幕宽高比
p.x *= r.x/r.y;
// 距离场:p到原点的距离。距离作为颜色返回
l = length(p);
// 采用一个循环为颜色赋值
for(int i=0;i<3;i++) {
uv+=p/l*(sin(z)+1.)*abs(sin(l*9.-z*2.));
c[i] =0.05/length(abs(fract(uv)-.5));
}
fragColor = vec4(c,t);
}