机器学习之MATLAB代码--PCA-LSTM模型（十二）

代码

1、

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行
%%  导入数据
X = xlsread('input');
Y = xlsread('output');
%% PCA主成分降维
[Z,MU,SIGMA]=zscore(X);

%% 计算相关系数矩阵
Sx=cov(Z);  % 相关系数矩阵计算

%% 计算相关系数矩阵的特征值特征向量
[V,D] = eig(Sx);   %计算相关系数矩阵的特征向量及特征值

eigValue = diag(D);  %将特征值提取为列向量

[eigValue,IX]=sort(eigValue,'descend');%特征值降序排序
eigVector=V(:,IX);                     %根据排序结果，特征向量排序

C=sort(eigValue,'descend');                        %特征值进行降序排序

rat1=C./sum(C)                       %求出排序后的特征值贡献率
rat2=cumsum(C)./sum(C)               %求出排序后的累计贡献率


result1(1,:)   = {'特征值','贡献率','累计贡献率'};      %细胞矩阵1第一行标题
result1(2:(length(D)+1),1) = num2cell(C);                      %将特征值放到第一列
result1(2:(length(D)+1),2) = num2cell(rat1);                   %将贡献率放到第二列
result1(2:(length(D)+1),3) = num2cell(rat2)                    %将累计贡放到第三列
%% 特征向量的归一化处理
norm_eigVector=sqrt(sum(eigVector.^2));%特征向量进行归一化处理
eigVector=eigVector./repmat(norm_eigVector,size(eigVector,1),1);

%% 判断贡献率
 %根据贡献率达到85%故选择
 d=7;% 这块根据实际情况修改

%% 数据降维处理
eigVector=eigVector(:,1:d); %求出对应特征向量
Y1=X*eigVector;              %处理样本和向量相乘获得降维数据
%% 赋值为原始X
X=Y1;
%% 训练集和预测集划分
% 训练集-
P_train= X((1:40),:)';%冒号代表取出来是整行或者整列，'代表转置
P_test = X((41:end),:)';
M = size(P_train,2);
% 测试集-
T_train= Y((1:40),:)';
T_test = Y((41:end),:)';
N = size(T_test,2);
%% 数据归一化
[P_train, ps_input] = mapminmax(P_train, 0, 1);
P_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%%  数据平铺
P_train =  double(reshape(P_train, 7, 1, 1, 40));
P_test  =  double(reshape(P_test , 7, 1, 1, 20));

t_train = t_train';
t_test  = t_test' ;

%%  数据格式转换
for i = 1 : M
    p_train{i, 1} = P_train(:, :, 1, i);
end

for i = 1 : N
    p_test{i, 1}  = P_test( :, :, 1, i);
end

%%  创建模型
layers = [
    sequenceInputLayer(7)              % 建立输入层
    
    lstmLayer(10, 'OutputMode', 'last') % LSTM层
    reluLayer                           % Relu激活层
    
    fullyConnectedLayer(1)         % 全连接层
    regressionLayer];                   % 回归层
 
%% 参数设置
options = trainingOptions('adam', ...     % Adam 梯度下降算法
    'MaxEpochs',1000,...                  % 最大训练次数1000
    'InitialLearnRate', 5e-3,...          % 初始学习率为0.005
    'LearnRateSchedule', 'piecewise',...  % 学习率下降
    'LearnRateDropFactor', 0.5,...        % 学习率下降因子 0.5
    'LearnRateDropPeriod', 900,...        % 经过900次训练后 学习率为 0.005*0.5
    'Shuffle', 'every-epoch',...          % 每次训练打乱数据集
    'Plots', 'training-progress',...      % 画出曲线
    'Verbose', false);

%%  训练模型
net = trainNetwork(p_train, t_train, layers, options);

%%  仿真预测
t_sim1 = predict(net, p_train);
t_sim2 = predict(net, p_test );

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1' - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2' - T_test ).^2) ./ N);
%% R2
R1 = 1 - norm(T_train - T_sim1')^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test -  T_sim2')^2 / norm(T_test -  mean(T_test ))^2;
%%  MAE
mae1 = sum(abs(T_sim1' - T_train)) ./ M ;
mae2 = sum(abs(T_sim2' - T_test )) ./ N ;

%%  绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'PCA-LSTM训练集预测结果对比'; ['(RMSE=' num2str(error1) 'R^2 =' num2str(R1) 'MAE =' num2str(mae1) ')']};
title(string)
xlim([1, M])
grid

figure
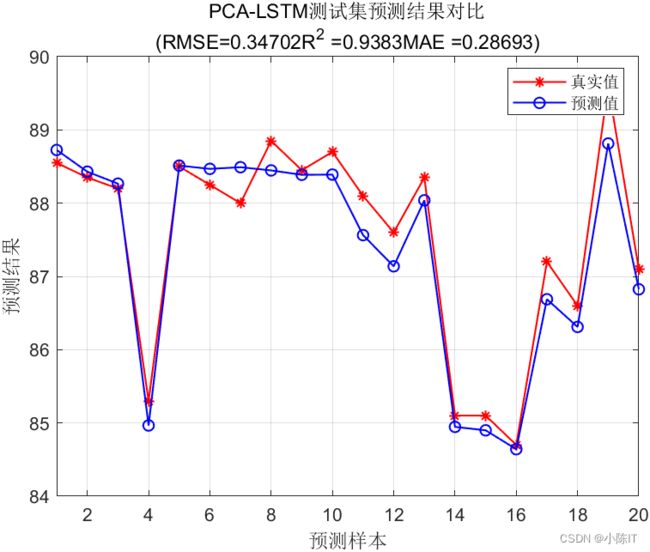
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'PCA-LSTM测试集预测结果对比';['(RMSE=' num2str(error2) 'R^2 =' num2str(R2)  'MAE =' num2str(mae2) ')']};
title(string)
xlim([1, N])
grid

%% 打印出模型评价指标
disp(['训练集数据的RMSEC为：', num2str(error1)])
disp(['测试集数据的RMSEP为：', num2str(error2)])

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])
%% 测试集误差图
figure  
plot(T_test'-T_sim2,'b-*', 'LineWidth', 1)
xlabel('测试集样本编号')
ylabel('预测误差')
title('PCA-LSTM测试集预测误差')
grid on;
legend('PCA-LSTM预测输出误差')

    

2、

function [z,mu,sigma] = zscore(x,flag,dim)
%ZSCORE Standardized z score for tall arrays
%   Z = ZSCORE(X)
%   [Z,MU,SIGMA] = ZSCORE(X)
%   [...] = ZSCORE(X,1)
%   [...] = ZSCORE(X,FLAG,DIM)
%
%   See also ZSCORE, MEAN, STD.

%   Copyright 2015 The MathWorks, Inc.

if nargin < 2
    flag = 0;
end

if nargin < 3
    % We can't determine dim for tall arrays as the size might not be
    % known. If not supplied, use the dimensionless versions.
    validateFlag(flag)
    mu = mean(x);
    sigma = std(x,flag);
else
    % User supplied dim
    validateFlag(flag)
    mu = mean(x,dim);
    sigma = std(x,flag,dim);
end

% Now standardize X to give Z, taking care when sigma is zero
sigma0 = sigma;
subs = struct('type','()','subs',{{sigma0==0}});
sigma0 = subsasgn(sigma0, subs, 1);

z = (x - mu) ./ sigma0;


function validateFlag(flag)
validateattributes(flag,{'numeric'}, {'integer','scalar','binary'}, 2);

3、

% 决定系数
function R2=eva1(T_train,T_sim1)

N = length(T_train);
R2=(N*sum(T_sim1.*T_train)-sum(T_sim1)*sum(T_train))^2/((N*sum((T_sim1).^2)-(sum(T_sim1))^2)*(N*sum((T_train).^2)-(sum(T_train))^2));

4、

%决定系数
function R2=eva1(T_test,T_sim2)

N = length(T_test);
R2=(N*sum(T_sim2.*T_test)-sum(T_sim2)*sum(T_test))^2/((N*sum((T_sim2).^2)-(sum(T_sim2))^2)*(N*sum((T_test).^2)-(sum(T_test))^2));

数据

结果

如有需要代码和数据的同学请在评论区发邮箱，一般一天之内会回复，请点赞＋关注谢谢！！