【LSTM回归预测】attention机制LSTM时间序列回归预测【含Matlab源码 1992期】
⛄一、attention机制LSTM预测
1 总体框架
数字货币预测模型分为两部分,由LSTM模块和Attention模块组成。
2 LSTM模块
长短期记忆网络(LSTM)是一种特殊的递归神经网络(RNN)模型,是为了解决RNN模型梯度消失的问题而提出的。在传统的RNN模型当中,当时间跨度较长时,网络权重更新会十分缓慢。针对此问题,LSTM采用了“记忆单元”来存储记忆。下图是LSTM的简单示意图。其中,一个LSTM网络主要包括以下几部分:记忆细胞(Ct)、遗忘门(ft)、输入门(it)、输出门(Ot)。
3 Attention模块
在实际过程中,长时间序列特征的重要程度往往存在差异,而LSTM神经网络对于长时间序列输入没有区分。数字货币价格随着各种因素的变化在不断变化,不同时间点的特征对于数字货币价格预测的影响程度是不同的。在时间序列数据的处理中,Attention机制对长短期记忆网络(LSTM)输出的隐藏层向量ht进行加权求和。此处的权重大小可以理解为“不同时间点上的特征的重要程度”。其中,Hi表示第i时刻输入序列的隐藏层的状态值。然后,我们通过相似性函数Score(Hi,Hk)获取最后一个隐藏层输出Hk与其他每个时间点隐藏层输出Hi的相似度得分ei。相似性函数计算公式如下:

其中,Dot表示采用点积的方式进行计算。然后,通过公式(8)的soft-max函数可以计算出每个时间点的不同的注意力权重ai,在此基础上计算注意力权重ai与隐藏层状态的乘积,即可得到Attention层的输出向量C。
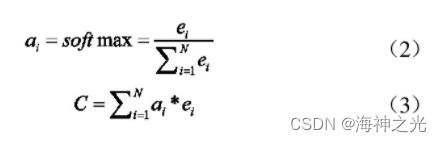
⛄二、部分源代码
% QRLSTM
% 数据集(列为特征,行为样本数目
% QRLSTM
% 数据集(列为特征,行为样本数目
clc
clear
close all
load(‘./Train.mat’)
%
Train(1,:) =[];
y = Train.demand;
x = Train{:,3:end};
[xnorm,xopt] = mapminmax(x’,0,1);
[ynorm,yopt] = mapminmax(y’,0,1);
x = x’;
xnorm = xnorm(:,1:1000);
ynorm = ynorm(1:1000);
k = 24; % 滞后长度
% 转换成2-D image
for i = 1:length(ynorm)-k
Train_xNorm(:,i,:) = xnorm(:,i:i+k-1);
Train_yNorm(i) = ynorm(i+k-1);
Train_y(i) = y(i+k-1);
end
Train_yNorm= Train_yNorm’;
ytest = Train.demand(1001:1170);
xtest = Train{1001:1170,3:end};
[xtestnorm] = mapminmax(‘apply’, xtest’,xopt);
[ytestnorm] = mapminmax(‘apply’,ytest’,yopt);
xtest = xtest’;
for i = 1:length(ytestnorm)-k
Test_xNorm(:,i,:) = xtestnorm(:,i:i+k-1);
Test_yNorm(i) = ytestnorm(i+k-1);
Test_y(i) = ytest(i+k-1);
end
Test_yNorm = Test_yNorm’;
clear k i x y
%
%% 训练集和验证集划分
TrainSampleLength = length(Train_yNorm);
validatasize = floor(TrainSampleLength * 0.1);
Validata_xNorm = Train_xNorm(:,end - validatasize:end,:);
Validata_yNorm = Train_yNorm(:,TrainSampleLength-validatasize:end);
Validata_y = Train_y(TrainSampleLength-validatasize:end);
Train_xNorm = Train_xNorm(:,1:end-validatasize,:);
Train_yNorm = Train_yNorm(:,1:end-validatasize);
Train_y = Train_y(1:end-validatasize);
%%
[params,~] = paramsInit(numhidden_units1,inputSize,outputSize); % 导入初始化参数
[~,validatastate] = paramsInit(numhidden_units1,inputSize,outputSize); % 导入初始化参数
[~,TestState] = paramsInit(numhidden_units1,inputSize,outputSize); % 导入初始化参数
% 训练相关参数
TrainOptions;
numIterationsPerEpoch = floor((TrainSampleLength-validatasize)/minibatchsize);
LearnRate = 0.01;
%% Loop over epochs.
figure
start = tic;
lineLossTrain = animatedline(‘color’,‘r’);
validationLoss = animatedline(‘color’,‘g’,‘Marker’,‘o’);
xlabel(“Iteration”)
ylabel(“Loss”)
% epoch 更新
iteration = 0;
for epoch = 1 : numEpochs
[~,state] = paramsInit(numhidden_units1,inputSize,outputSize); % 每轮epoch,state初始化
disp(['Epoch: ', int2str(epoch)])
% batch 更新
for i = 1 : numIterationsPerEpoch
dlX = gpuArray(Train_xNorm(:,idx,:));
dlY = gpuArray(Train_yNorm(idx));
[gradients,loss,state] = dlfeval(@Model2,dlX,dlY,params,state);
% L2正则化
% L2regulationFactor = 0.000011;
% gradients = dlupdate( @(g,parameters) L2Regulation(g,parameters,L2regulationFactor),gradients,params);
% gradients = dlupdate(@(g) thresholdL2Norm(g, gradientThreshold),gradients);
[params,averageGrad,averageSqGrad] = adamupdate(params,gradients,averageGrad,averageSqGrad,iteration,LearnRate);
% 验证集测试
if iteration == 1 || mod(iteration,validationFrequency) == 0
output_Ynorm = ModelPredict(gpuArray(Validata_xNorm),params,validatastate);
lossValidation = mse(output_Ynorm, gpuArray(Validata_yNorm));
end
% 作图(训练过程损失图)--------------------------********————————————————————————————————————————————————
end
% 每轮epoch 更新学习率
if mod(epoch,5) == 0
LearnRate = LearnRate * LearnRateDropFactor;
end
end
%% 训练集
Predict_yNorm = Model2Predict(gpuArray(Train_xNorm),params,TestState);
Predict_yNorm = extractdata(Predict_yNorm);
Predict_y = mapminmax(‘reverse’,Predict_yNorm,yopt);
%
figure
plot(Predict_y,‘r’);
hold on
plot(Train_y,‘g’)
legend(‘训练集预测值’,‘训练集实际值’)
%% 验证集
Predict_yNorm = Model2Predict(gpuArray(Validata_xNorm),params,TestState);
Predict_yNorm = extractdata(Predict_yNorm);
Predict_y = mapminmax(‘reverse’,Predict_yNorm,yopt);
%
figure
plot(Predict_y,‘r’);
hold on
plot(Validata_y,‘g’)
legend(‘验证集预测值’,‘验证集实际值’)
%% predict(测试集)
Predict_yNorm = Model2Predict(gpuArray(Test_xNorm),params,TestState);
Predict_yNorm = extractdata(Predict_yNorm);
Predict_y = mapminmax(‘reverse’,Predict_yNorm,yopt);
%
figure
plot(Predict_y,‘r’);
hold on
plot(Test_y,‘g’)
legend(‘测试集预测值’,‘测试集实际值’)
## ⛄三、运行结果
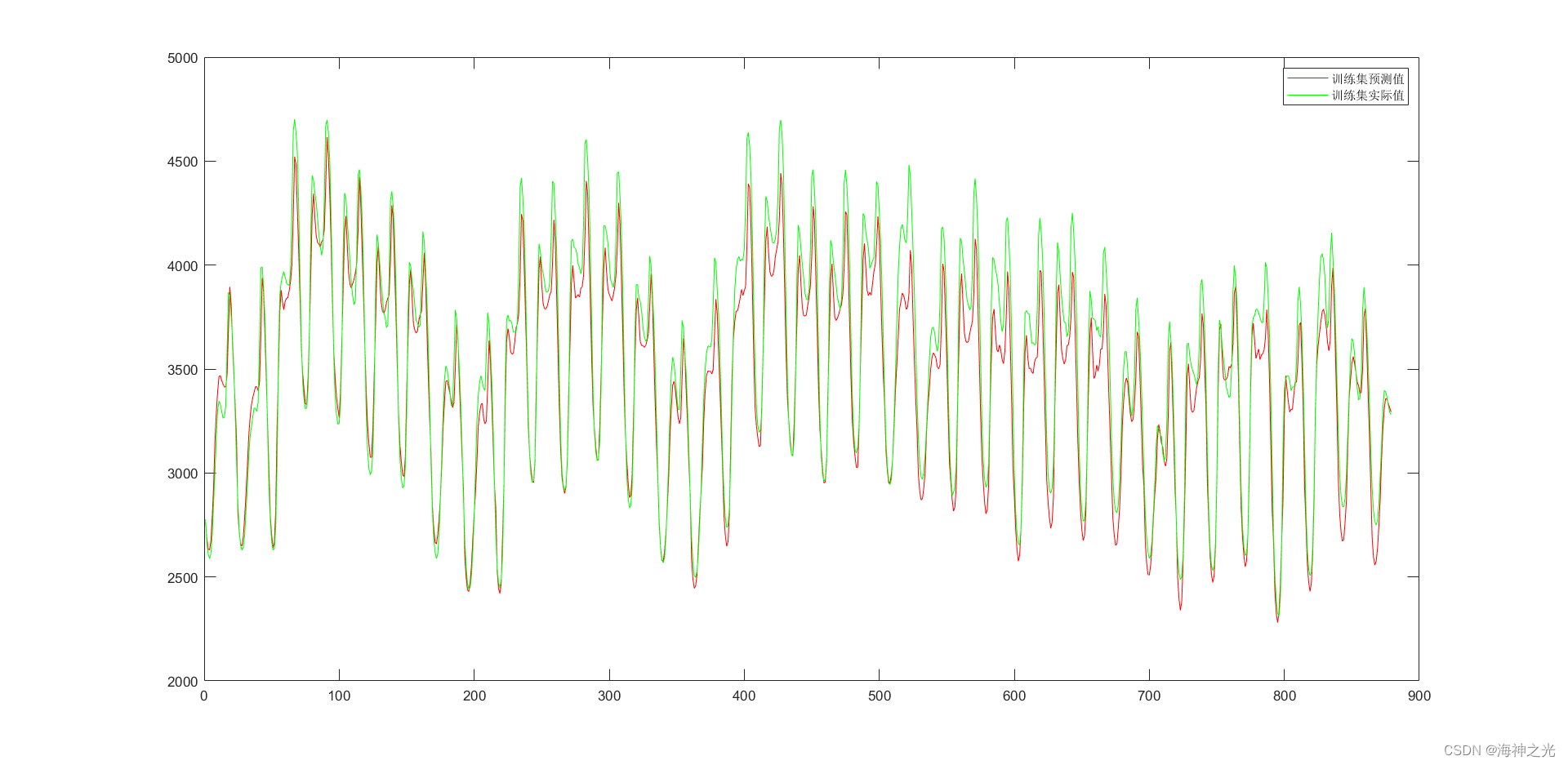
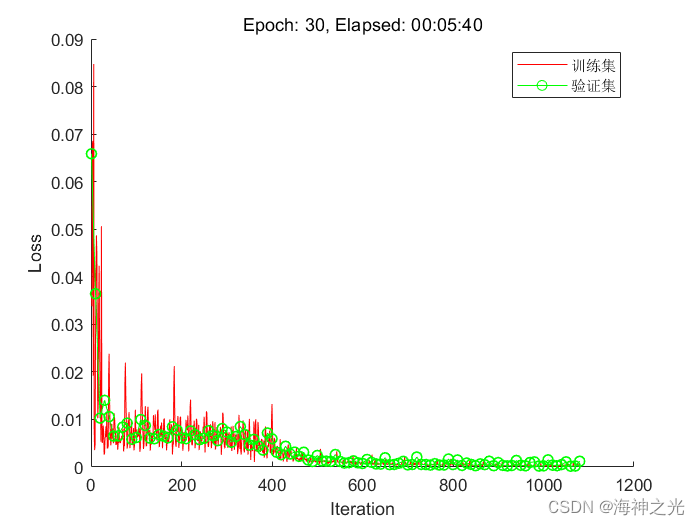
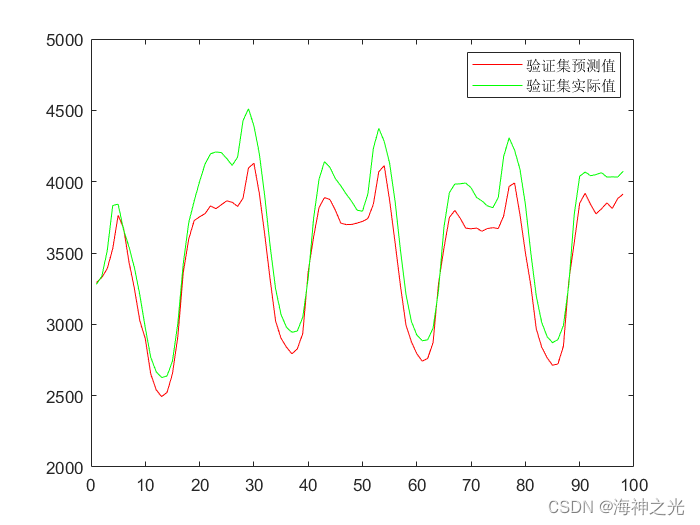
## ⛄四、matlab版本及参考文献
**1 matlab版本**
2014a
**2 参考文献**
[1] 万浩睿,李成林,赵开明,王睿林.基于Attention机制的LSTM数字货币预测模型[J].长江信息通信. 2022,35(05)
**3 备注**
简介此部分摘自互联网,仅供参考,若侵权,联系删除