图神经网络task2——消息传递

1、消息传递范式

消息传递是实现GNN的一种通用框架和编程范式。它从聚合与更新的角度归纳总结了多种GNN模型的实现，它的思路是：

• 首先结合边的特征以及和边相连的两个节点的特征，得到消息函数；
• 把和节点u相连的边上的信息函数聚合起来，并结合u的已有节点特征，来更新v的节点特征。

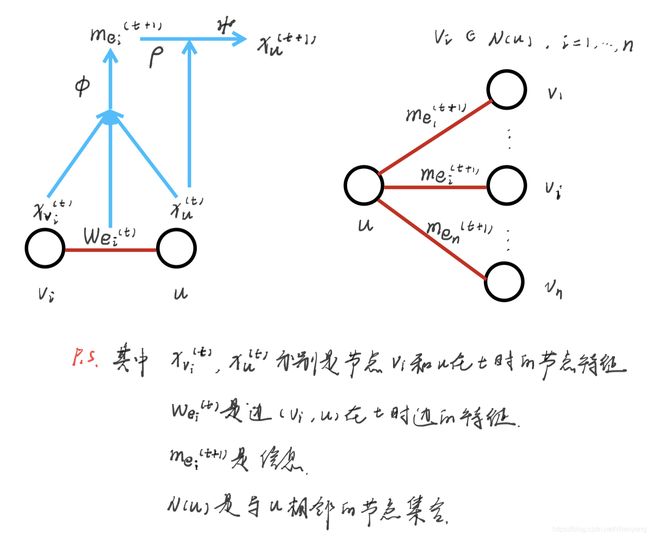
消息传递的数学公式如下：
$$\begin{array}{rl}{m}_{e_i}^{t+1}& =\Phi (x_{v_i}^t,x_u^t,{\omega }_{e_i}^t)\\ x_u^{t+1}& =\Psi (x_u^t,\rho (\{m_{e_i}^{t+1},i\in N(u)\})\end{array}$$

• 其中$\Phi$是定义在每条边上的消息函数，它将边上特征与其两端节点的特征相结合来生成消息，一般是可微分的函数；
• 其中$\rho$是聚合函数，把所有的边的消息聚合起来处理，通常是可微分、具有排列不变性的函数（即和$m_{e_i}^{t+1}$的顺序无关）；
• 其中$\Psi$是更新函数，结合聚合后的消息和节点本身的特征来更新节点的特征；
• 从上述公式可以看出，消息函数、聚合函数和更新函数都是不确定的，可以根据需要设置不同的函数形式。

\quad

2、MessagePassing基类

Pytorch Geometric(PyG)提供了MessagePassing基类，它封装了“消息传递”的运行流程。通过继承MessagePassing基类，可以方便地构造消息传递图神经网络。而关键地就是如上文所说，定义消息函数、聚合函数和更新函数，下面先介绍一下MP基类和该类的一些方法。
\quad

2.1、MP类和基本方法

• MessagePassing(arrr = "add", flow = "source_to_target", node_dim = -2)
  • arr: 定义聚合函数，默认求和，可选mean和max；
  • flow: 是消息传递的方向，默认从源节点到目标节点，可选target_to_source.
    \quad
• MessagePassing.message()
  • 实现消息函数$\Phi$的定义与结果传出，参数需根据要求自定；
  • 首先确定需要传递消息的边的集合，并且定义出消息函数.
    \quad
• MessagePassing.propagate(edge_index, size: Size = None, **kwargs)
  • 开始传递消息的起始调用，在此方法中message、update等方法被调用；
  • edge_index: 是存储边的张量；
    \quad
• MessagePassing.aggregate(...)
  • 定义聚合函数$\rho$。
    \quad
• MessagePassing.update(aggr_out, ...)
  • 定义并实现更新函数$\Psi$；
  • 此方法以aggregate方法的输出为第一个参数，并接收所有传递给propagate()方法的参数。

函数调用流程如下（不执行mp.message_and_aggregate的情况下）：

\quad

3、MessagePassing实例

我们以继承MessagePassing基类的GCNConv类为例，学习如何通过继承MessagePassing基类来实现一个简单的图神经网络。

3.1、三个函数的数学定义

• 消息函数：
  $$m_{e_j}^{t+1}=\Phi (x_{v_j}^t,x_u^t,{\omega }_{e_j}^t)=\frac{1}{\sqrt{deg(j)}}\cdot \frac{1}{\sqrt{deg(u)}}\Theta \cdot x_j^t$$

• 聚合函数
  $$\rho =\sum _{j\in N(u)}{m}_{e_j}^{t+1}$$

• 更新函数：
  $$\Psi (\rho )=\rho$$

由上可知：
$$x_u^{t+1}=\sum _{j\in N(u)}\frac{1}{\sqrt{deg(j)}}\cdot \frac{1}{\sqrt{deg(u)}}\Theta \cdot x_j^t$$

3.2、GCNConv实现步骤

（1）向邻接矩阵添加自环边

主要通过torch_geometric.utils.add_self_loops方法实现。

def add_self_loops(edge_index, edge_weight: Optional[torch.Tensor] = None,
                   fill_value: float = 1., num_nodes: Optional[int] = None):
                   pass
                   return edge_index, edge_weight

• 这一步相当于是对邻接矩阵的预处理，即增加节点的自身循环，即在邻接矩阵中把对角线上的补上1，在torch中就是把$(i,i)$加到edge_index中；
• 如果是有权图，即edge_weight不是None，加入的自环边权重补充为1，即fill_value；
• 函数返回处理好的edge_index和edge_weight；
• num_nodes即节点数量。
  \quad

（2）对节点的特征矩阵进行线性变换

这一步就对应了$\Theta \cdot x_j^t$，主要通过一个线性层torch.nn.Linear实现。
\quad

（3）对变换后的节点特征进行标准化

也就是算$d_{ij}=\frac{1}{\sqrt{deg(i)}}\cdot \frac{1}{\sqrt{deg(j)}}$，然后得到一个张量norm，里面元素的个数和扩充过得edge_index中边的个数相等，且对应，即：若edge_index的第k个边为$(i,j)$，norm中第k个为$d_{ij}$。
而对于节点的度可以使用torch_geometric.utils.degree获得

degree(index, num_nodes: Optional[int] = None, dtype: Optional[int] = None)

对于节点的次，上述函数是通过统计index里面的各节点的个数得到的。
在GCNconv的实现过程中，这一部分的代码如下：

row, col = edge_index
deg = degree(col, x.size(0), dtype=x.dtype)
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

• 这里是采用终止节点的列表计算点的度，在无向图中，采用row和col没有区别；
• 在有向图中，采用row呢，是初始节点，这时计算出的是出次，而对于col算出来的即入次，两者往往不相同。

实例，对于如下的图，我们分别使用row和col计算度数，看看有什么区别：

import torch
from torch_geometric.data import Data
from torch_geometric.utils import degree,add_self_loops

print(edge_index)
edge_index2,_ = add_self_loops(edge_index,num_nodes = 5)
print(edge_index2)
'''
tensor([[0, 4, 3, 1, 1, 0],
        [4, 3, 2, 2, 0, 1]])
tensor([[0, 4, 3, 1, 1, 0, 0, 1, 2, 3, 4],
        [4, 3, 2, 2, 0, 1, 0, 1, 2, 3, 4]])
'''

#下面分别使用row和col计算度
r2,c2 = edge_index2
print(r2)
print(c2)
'''
tensor([0, 4, 3, 1, 1, 0, 0, 1, 2, 3, 4])
tensor([4, 3, 2, 2, 0, 1, 0, 1, 2, 3, 4])
'''
d_out = degree(r2,5)
print("d_out:",d_out)
d_in = degree(c2,5)
print("d_in :",d_in)
'''
d_out: tensor([3., 3., 1., 2., 2.])
d_in : tensor([2., 2., 3., 2., 2.])
'''

\quad

（4）归一化j中的节点特征

也就是把上一步norm中的$d_{ij}$（相当于j节点的权重了）和对应的$\Theta \cdot x_j^t$乘起来就搞定了。
\quad

（5）将节点特征求和

这一步就是聚合函数了，把上一步中的全部加起来就好了。

\quad

参考文献

1、【深度学习实战】Pytorch Geometric实践——利用Pytorch搭建GNN
2、消息传递图神经网络