python 使用张量进行线性回归 (带绘图)
本文章包含以下内容:
1.生成数据集
根据带有噪声的线性模型生成一个含有1000个样本的数据集,每个样本包含从标准正态分布中采样的2个特征,使用线性模型参数w=[2,-3.4]T,b=4.2和噪声项e生成数据集及其标签: y=Xw+b+e,将e视为模型预测和标签时的潜在观测误差,其中e服从均值为0且标准差为0.01的正态分布。
定义函数synthetic_data(w, b, num_examples)生成数据集x与y,其中w、b 与num_examples分别为权值﹑阈值与样本个数。
2.读取数据集
定义一个data_iter函数,该函数接收批量大小﹑特征矩阵和标签向量作为输入,生成大小为batch_size的小批量,每个小批量包含一组特征和标签。定义函数data_iter(batch_size, features, labels)实现。
3.初始化模型参数
使用小批量随机梯度下降优化模型参数前,通过从均值为0﹑标准差为0.01的正态分布中采样随机数来初始化权重,并将偏置初始化为0。
4.定义模型
定义函数linreg,其中输入特征为X﹑权重为w和偏置b,即 linreg(X,w,b)。
5.定义损失函数
定义平方损失函数squared_loss(y_hat, y)返回损失值,其中y_hat为预测值,y为真实值。
6.定义优化算法
从数据集中随机抽取小批量样本,根据参数计算损失的梯度;然后朝着减少损失的方向更新参数。定义函数sgd(params, Ir, batch_size)实现小批量随机梯度下降更新,该函数接受模型参数集合﹑学习速率和批量大小作为输入。每一步更新的大小由学习速率lr决定,用批量大小(batch_size)来规范化步长。
7.训练
lr = 0.03
num_epochs = 3net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for ×, y in data_iter(batch_size, features, labels):l = loss(net(X, w, b), y)#×和y的小批量损失
#因为I形状是(batch_size,1),而不是一个标量○l中的所有元素被加到一起,
#并以此计算关于[w,b]的梯度
l.sum().backward()
sgd([w,b], Ir, batch_size)#使用参数的梯度更新参数with torch.no_grad():
train_l = loss(net(features, w,b),labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
代码如下:
import numpy as np
import matplotlib.pyplot as plt
import torch
# 按xw+b+e生成数据集,输入w(列表),b,标准差,样本个数 num_examples ,e为均值 0,标准差 0.01,符合正态分布的误差
def synthetic_data(w, b, num_examples):
# rand随即产生0-1之间的数字填充在创建的张量中
# 数据是num_examples*len(w)的矩阵
X = torch.rand(num_examples, len(w))
# y = Xw + b + e
y = torch.matmul(X, w) + b
# np.random.normal生成size个均值为loc,标准差为scale,正态分布的随机数
y += np.random.normal(loc=0, scale=0.01, size=num_examples)
# print(X, y.reshape((-1, 1)))
# y是行向量,要转为列向量。
return X, y.reshape((-1, 1))
# 初始化参数 通过从均值为0﹑标准差为0.01的正态分布中采样随机数来初始化权重
# 并将偏置初始化为0。
def chushi():
# 返回从正态分布中提取的随机数的张量,该正态分布的均值是mean,标准差是std。
# requires_grad=True 表示需要计算梯度,注意size=(2,1)列向量
w = torch.normal(mean=0, std=0.01, size=(2, 1), requires_grad=True)
# 返回一个类型为torch.dtype,值为0的tensor
b = torch.zeros(1, requires_grad=True)
return w, b
# 该函数接收批量大小﹑特征矩阵和标签向量作为输入,生成大小为batch_size的小批量,每个小批量包含一组特征和标签。
def data_iter(batch_size, features, labels): # 批量 特征 标签
for i in range(len(labels) - 4):
# print(features[i:i + 4], labels[i:i + 4])
# yield 可以看成 return,只是下回调用从这里开始
yield features[i:i + 4], labels[i:i + 4] # 每次取四个来输出
# 模型 输入特征为×﹑权重为w和偏置b
def linreg(X, w, b):
# 张量无法用下面的代码计算相乘
# sum = []
# for i in range(len(X)):
# sum.append([np.dot(w, X[i]) + b])
# print(sum)
# return torch.Tensor(sum)
# =======================================
# print(torch.matmul(X, w)+b)
# 张量乘积 torch.matmul()
return torch.matmul(X, w) + b # 这里X(4*2)w(2*1)
# 平方损失函数,返回损失值,其中y_hat为预测值, y为真实值。
def squared_loss(y_hat, y):
# 使用如下代码会没有梯度
# sum = []
# for i in range(len(y)):
# sum.append([(y[i] - y_hat[i]) ** 2])
# # print(torch.tensor(sum, requires_grad=True))
# # 使用 tensor 可以设置 requires_grad=True ,Tensor不能设置。
# return torch.tensor(sum, requires_grad=True)
# ============================================
# 平方损失
# print((y - y_hat) ** 2)
return (y - y_hat) ** 2
# 从数据集中随机抽取小批量样本,根据参数计算损失的梯度;然后朝着减少损失的方向更新参数。
# 实现小批量随机梯度下降更新,该函数接受模型参数集合﹑学习速率和批量大小作为输入。
def sgd(params, lr, batch_size):
# wi_new = wi - lr * g(wi)
for param in params:
# print(param.grad)
param.data = param - lr * param.grad / batch_size
param.grad.zero_() # 梯度清零
def xunlian(batch_size, features, labels, w, b):
lr = 0.03 # 学习率
num_epochs = 3 # 循环次数
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # X和y 的小批量损失
# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,
# 并以此计算关于[w,b]的梯度
l.sum().backward()
# print(l)
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
# 创建数据集时,y用张量相乘创建,所以必须用张量
w = torch.tensor([2, -3.4])
b = 4.2
[X, y] = synthetic_data(w, b, 1000) # 生成数据集
# print(X,'\n',y)
w, b = chushi() # 初始化 w, b
batch_size = 4 # 批量大小为 4
xunlian(batch_size, X, y, w, b) # 训练函数
# print(w, b)
# 绘图 =============================================
# 定义图像和三维格式坐标轴
fig = plt.figure()
m = plt.axes(projection='3d') # 绘制3d图形
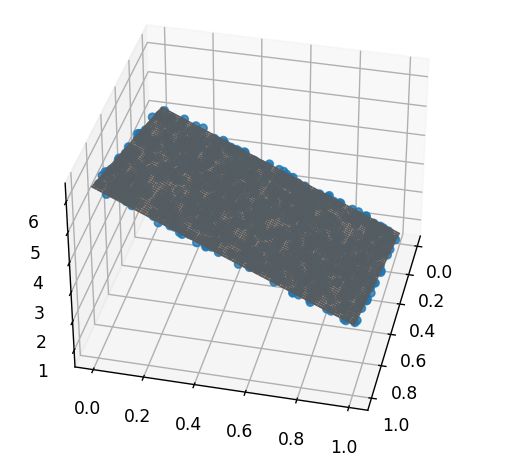
m.scatter3D(X[:, 0], X[:, 1], y, alpha=0.8) # 绘制散点图
xl = np.linspace(0, 1, ) # 绘制回归曲面(平面)
yl = np.linspace(0, 1, )
xl, yl = np.meshgrid(xl, yl, indexing='ij')
w = w.tolist() # 张量转为列表,用于绘图
b = b.tolist()
zl = w[0][0] * xl + w[1][0] * yl + b
m.plot_surface(xl, yl, zl, color='Grey', ) # 三维画面
print('真实的 w 和 b:\nw = [2, -3.4]\nb = [4.2]')
print('回归的 w 和 b:\nw =', w, '\nb =', b)
plt.show() # 显示
注释删掉行数减一半。
结果示例:
epoch 1, loss 0.001588
epoch 2, loss 0.000102
epoch 3, loss 0.000099
真实的 w 和 b:
w = [2, -3.4]
b = [4.2]
回归的 w 和 b:
w = [[1.9990111589431763], [-3.3990085124969482]]
b = [4.198093891143799]
如果觉着平面难看,可以删去 112~118 行。
plt.show() # 显示
需要保留才能显示图像。
代码更改:
1.
def synthetic_data(w, b, num_examples):
生成数据集函数中x改为正态分布
2.
def data_iter(batch_size, features, labels): # 批量 特征 标签
打包函数中增加随机选取
import numpy as np
import matplotlib.pyplot as plt
import torch
# 按xw+b+e生成数据集,输入w(列表),b,标准差,样本个数 num_examples ,e为均值 0,标准差 0.01,符合正态分布的误差
def synthetic_data(w, b, num_examples):
# normal返回从单独的正态分布中提取的随机数的张量,该正态分布的均值是0,标准差是0.1。
# 数据是num_examples*len(w)的矩阵
X = torch.normal(0, 1, (num_examples, len(w)))
# y = Xw + b + e
y = torch.matmul(X, w) + b
# np.random.normal生成size个均值为loc,标准差为scale,正态分布的随机数
y += np.random.normal(loc=0, scale=0.01, size=num_examples)
# print(X, y.reshape((-1, 1)))
# y是行向量,要转为列向量。
return X, y.reshape((-1, 1))
# 初始化参数 通过从均值为0﹑标准差为0.01的正态分布中采样随机数来初始化权重
# 并将偏置初始化为0。
def chushi():
# 返回从正态分布中提取的随机数的张量,该正态分布的均值是mean,标准差是std。
# requires_grad=True 表示需要计算梯度,注意size=(2,1)列向量
w = torch.normal(mean=0, std=0.01, size=(2, 1), requires_grad=True)
# 返回一个类型为torch.dtype,值为0的tensor
b = torch.zeros(1, requires_grad=True)
return w, b
# 该函数接收批量大小﹑特征矩阵和标签向量作为输入,生成大小为batch_size的小批量,每个小批量包含一组特征和标签。
def data_iter(batch_size, features, labels): # 批量 特征 标签
for i in range(len(labels) - 4):
# print(features[i:i + 4], labels[i:i + 4])
# yield 可以看成 return,只是下回调用从这里开始
# yield features[i:i + 4], labels[i:i + 4] # 每次取四个来输出
# np.random.choice()产生随机数
test_index = np.random.choice(len(features), batch_size, replace=False)
# print(features[test_index], labels[test_index])
yield features[test_index], labels[test_index]
# 模型 输入特征为×﹑权重为w和偏置b
def linreg(X, w, b):
# 张量无法用下面的代码计算相乘
# sum = []
# for i in range(len(X)):
# sum.append([np.dot(w, X[i]) + b])
# print(sum)
# return torch.Tensor(sum)
# =======================================
# print(torch.matmul(X, w)+b)
# 张量乘积 torch.matmul()
return torch.matmul(X, w) + b # 这里X(4*2)w(2*1)
# 平方损失函数,返回损失值,其中y_hat为预测值, y为真实值。
def squared_loss(y_hat, y):
# 使用如下代码会没有梯度
# sum = []
# for i in range(len(y)):
# sum.append([(y[i] - y_hat[i]) ** 2])
# # print(torch.tensor(sum, requires_grad=True))
# # 使用 tensor 可以设置 requires_grad=True ,Tensor不能设置。
# return torch.tensor(sum, requires_grad=True)
# ============================================
# 平方损失
# print((y - y_hat) ** 2)
return (y - y_hat) ** 2
# 从数据集中随机抽取小批量样本,根据参数计算损失的梯度;然后朝着减少损失的方向更新参数。
# 实现小批量随机梯度下降更新,该函数接受模型参数集合﹑学习速率和批量大小作为输入。
def sgd(params, lr, batch_size):
# wi_new = wi - lr * g(wi)
for param in params:
# print(param.grad)
param.data = param - lr * param.grad / batch_size
param.grad.zero_() # 梯度清零
def xunlian(batch_size, features, labels, w, b):
lr = 0.03 # 学习率
num_epochs = 3 # 循环次数
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # X和y 的小批量损失
# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,
# 并以此计算关于[w,b]的梯度
l.sum().backward()
# print(l)
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
# 创建数据集时,y用张量相乘创建,所以必须用张量
w = torch.tensor([2, -3.4])
b = 4.2
[X, y] = synthetic_data(w, b, 1000) # 生成数据集
# print(X,'\n',y)
w, b = chushi() # 初始化 w, b
batch_size = 4 # 批量大小为 4
xunlian(batch_size, X, y, w, b) # 训练函数
# print(w, b)
# 绘图 =============================================
# 定义图像和三维格式坐标轴
fig = plt.figure()
m = plt.axes(projection='3d') # 绘制3d图形
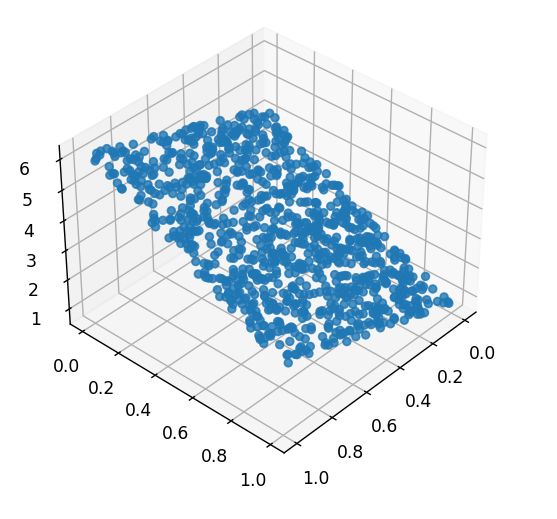
m.scatter3D(X[:, 0], X[:, 1], y, alpha=0.8) # 绘制散点图
xl = np.linspace(-2, 2, num=10) # 绘制回归曲面(平面)
yl = np.linspace(-2, 2, num=10)
xl, yl = np.meshgrid(xl, yl, indexing='ij')
w = w.tolist() # 张量转为列表,用于绘图
b = b.tolist()
zl = w[0][0] * xl + w[1][0] * yl + b
m.plot_surface(xl, yl, zl, color='Grey', ) # 三维画面
print('真实的 w 和 b:\nw = [2, -3.4]\nb = [4.2]')
print('回归的 w 和 b:\nw =', w, '\nb =', b)
plt.show() # 显示
结果示例:
epoch 1, loss 0.000105
epoch 2, loss 0.000103
epoch 3, loss 0.000102
真实的 w 和 b:
w = [2, -3.4]
b = [4.2]
回归的 w 和 b:
w = [[2.0002458095550537], [-3.4005370140075684]]
b = [4.199899673461914]