7月30日Pytorch笔记——识别手写数字初体验

---

前言

本文为7月30日Pytorch笔记，分为三个章节：

• Pytorch 常用网络层；
• 简单实现 Linear Regression；
• 识别手写数字。

---

一、Pytorch 常用网络层

• nn.Linear;
• nn.Conv2d;
• nn.LSTM;
• nn.ReLU;
• nn.Simoid;
• nn.Softmax;
• nn.CrossEntropyLoss;
• nn.MSE.

---

二、简单实现 Linear Regression

• $Loss=(wx+b-y{)}^2$:

def compute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (w*x + b))**2
    return totalError / float(len(points))

• Gradient descent: $w^{t+1}=w^t-\eta \frac{\partial Loss}{\partial w}$:

def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
        w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

• Iterate to optimize:

ef gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):
    b = starting_b
    m = starting_m
    for i in range(num_iterations):
        b, m = step_gradient(b, m, np.array(points), learning_rate)
    return [b, m]

---

三、识别手写数字

• MNIST:
  • 每个数字有 7000 张图片；
  • train/test splitting: 60k vs. 10k

$$\begin{gathered} X=[v^1,v^2,\dots ,v^{784}] \\ {H}_1=relu(X{W}_1+b_1) \\ {H}_2=relu(H_1{W}_2+b_2) \\ {H}_3=relu(H_2{W}_3+b_3) \\ Y:[0/1/\dots /9] \end{gathered}$$
$$\begin{gathered} pred=W_3\ast \{W_2[W_{1}X+b_1]+b_2\}+b_3 \\ objective=\sum (pred-Y{)}^2 \end{gathered}$$
代码如下：

import torch
from torch import nn
from torch.nn import functional as F
from torch import optim

import torchvision
from matplotlib import pyplot as plt

from utils import plot_image, plot_curve, one_hot

batch_size = 512

# Step 1: load dataset
train_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data', train=True, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=True)

test_loader = torch.utils.data.DataLoader(
    torchvision.datasets.MNIST('mnist_data/', train=False, download=True,
                               transform=torchvision.transforms.Compose([
                                   torchvision.transforms.ToTensor(),
                                   torchvision.transforms.Normalize(
                                       (0.1307,), (0.3081,))
                               ])),
    batch_size=batch_size, shuffle=False)

x, y = next(iter(train_loader))
print(x.shape, y.shape, x.min(), x.max())

plot_image(x, y, 'image sample')

# Step 2
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()

        # xw + b
        self.fc1 = nn.Linear(28*28, 256)
        self.fc2 = nn.Linear(256, 64)
        self.fc3 = nn.Linear(64, 10)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)

        return x

# Step 3: Training
net = Net()
# [w1, b1, w2, ]
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)
train_loss = []


for epoch in range(3):
    for batch_idx, (x, y) in enumerate(train_loader):
        x = x.view(x.size(0), 28*28)
        out = net(x)
        y_onehot = one_hot(y)
        # loss = mse(out, y_onehot)
        loss = F.mse_loss(out, y_onehot)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        train_loss.append(loss.item())

        if batch_idx % 10 == 0:
            print(epoch, batch_idx, loss.item())

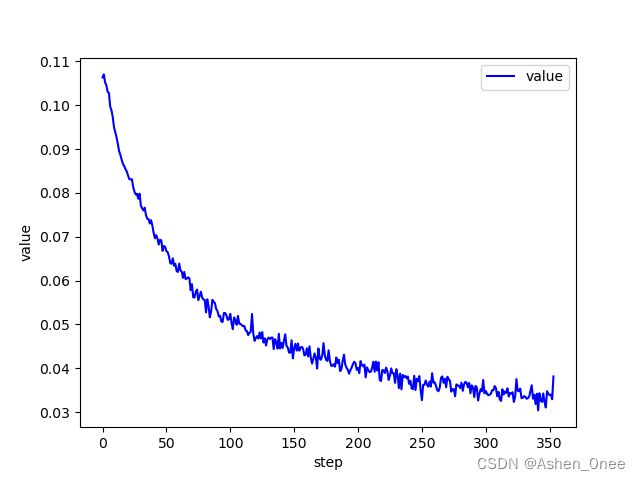
plot_curve(train_loss)
# got [w1, b1, w2, b2, w3, b3]

# Step 4: Accuracy
total_correct = 0

for x, y in test_loader:
    x = x.view(x.size(0), 28*28)
    out = net(x)
    pred = out.argmax(dim=1)
    correct = pred.eq(y).sum().float().item()
    total_correct += correct

total_num = len(test_loader.dataset)
acc = total_correct / total_num
print('test ass: ', acc)

x, y = next(iter(test_loader))

out = net(x.view(x.size(0), 28*28))
pred = out.argmax(dim=1)
plot_image(x, pred, 'test')

>>> test ass:  0.8856

---