【PyTorch】PyTorch深度学习实践|视频学习笔记|P6-P9
PyTorch深度学习实践
逻辑斯蒂回归及实现
- 背景与概念
- 基于分类问题中属性是类别性的,所以不能采取基于序数的线性回归模型,而提出了新的分类模型——逻辑斯蒂回归模型,输出每个样本在各个预测值上的概率值。
- 为了将最终的输出值控制在概率值P∈[0,1]的合理范围中,需要在线性单元输出后再加上一个非线性映射,这里我们使用饱和函数sigmoid
- 因为模型发生了变化,损失值的计算方式也要发生相应的变化;因为线性回归模型只需要比较两个实数之间的差异,所以可以使用均方误差值衡量;但是逻辑回归得到的结果是在描述事件的概率分布,因此我们的误差函数也变成比较两个分布之间的差异,这里我们使用交叉熵计算公式。
- 代码实现
import numpy as np
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
#二分类问题的输出值往往是0或1
x_data = torch.tensor([[1.0],[2.0],[3.0]])
y_data = torch.tensor([[0.0],[0.0],[1.0]])
#构建训练模型
class LogisticRegressionModel(torch.nn.Module):
def __init__(self):
super(LogisticRegressionModel,self).__init__()#这一块和线性回归的模型差距不大,因为sigmoid函数是无参数的,不需进行初始化
self.linear = torch.nn.Linear(1,1)
def forward(self,x):
y_pred = F.sigmoid(self.linear(x))#比线性回归模型就多了一步非线性映射
return y_pred
model = LogisticRegressionModel()
#构建损失函数的计算和优化器
criterion = torch.nn.BCELoss(size_average = False)#逻辑回归模型适用二分类交叉熵损失函数
op = torch.optim.SGD(model.parameters(),lr = 0.01)
epochs = []
costs = []
#训练过程,对每个优化器都进行尝试
for epoch in range(1000):
epochs.append(epoch)
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
costs.append(loss.item())
print(epoch, loss.item())
op.zero_grad()
loss.backward()
op.step()
# 对训练结果进行输出
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())
# 进行模型测试
X = np.linspace(0,10,200)
x_test = torch.Tensor(X).view(200,1)
y_test = model(x_test)
Y = y_test.data.numpy()
plt.ylabel('Probability of Pass')
plt.xlabel('Hours')
plt.plot(X, Y)
plt.grid()
plt.show()
# 训练过程可视化
plt.ylabel('Cost')
plt.xlabel('Epoch')
plt.plot(epochs, costs)
plt.show()
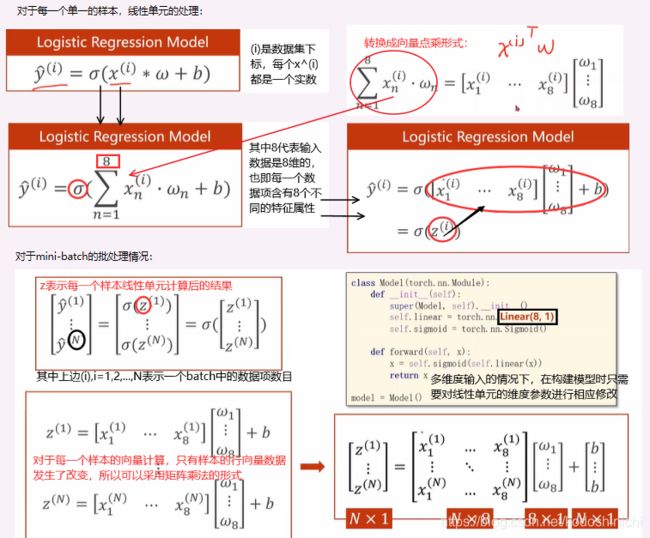
多维特征的输入
- 输入特征的变化
所谓输入特征的维度变化,影响的只是线性单元中控制输入维度的那一个参数 ;
在之前讲的例子中,每一个线性单元所做的工作即对一个实数输入x,乘上一个权重之后再加上一个偏置项,(之后再进行非线性映射),在这种情况下——输入的数据维度是1,线性单元的权重维度也是1x1大小的;
在实际的问题中,一个数据项含有多种特征属性且都与该问题相关联,此时我们输入的不再是一个实数,而是一个向量,同样权重单元也不再是1x1的,而也应该是一个相应维度的向量;输入与权重的运算就转换成向量之间的点乘运算,数与数之间的四则运算也同理转换成向量/矩阵的四则运算。
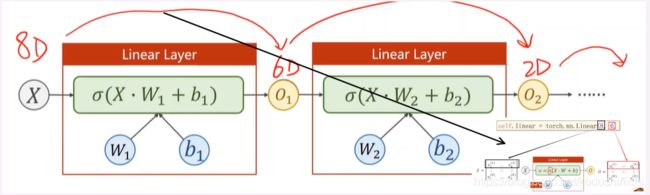
- 神经网络的本质:找到合适的空间变换
①从前面的讨论中,我们不难发现,如果将一个M维的数据传入线性计算单元,得到N维的输出,那么实际上是在做一个矩阵线性变换——从M维空间映射到N维空间。
②神经网络的学习面向的大多是现实社会中的问题,大多是要找到不同维度空间的非线性映射,我们采用将一层线性映射分解成多层线性映射(这不会改变线性映射的性质)并在每一层映射后加入非线性变换,以拟合现实生活中可能出现的各种复杂的变化情况。
对于程序编写来说,多维特征的数据输入,只在数据集构造和模型构造的代码上会有些许的改动。
#多维输入的模型构造
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear = torch.nn.Linear(8,1) #明确了输入数据是8维的,输出数据是1维的,从而定义了权重矩阵的维度
self.sigmoid = torch.nn.Sigmoid() #增加非线性映射
def forward(self,x):
y_pred = self.sigmoid(self.linear(x))
return y_pred
model = Model()
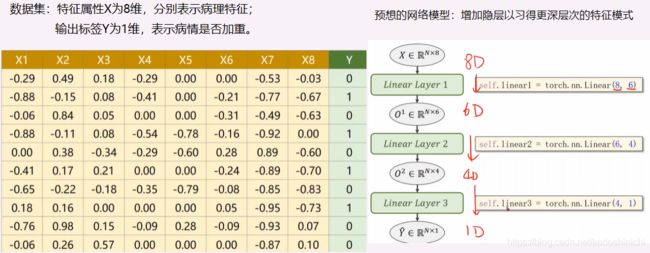
- 应用实例——构建网络度实现糖尿病病情预测
【功能实现】
①在准备数据集上,注意把导入的数据集的X值和Y标签进行区分;
②在构建模型上,这里使用的Sigmoid是直接继承自nn.Module模块下的一个模块;作为一个非线性映射层,是可以在后面构建计算图的时候进行复用的;
③虽然数据维度和网络结构发生了变化,但因为最后的输出仍然是一维的概率值,所以损失函数和优化器和之前的单层逻辑回归相比,并未发生改变。
import numpy as np
import torch
import matplotlib.pyplot as plt
#准备数据
x_data = torch.from_numpy(np.loadtxt('diabetes_data.csv.gz',delimiter=' ',dtype=np.float32))
y_data = torch.from_numpy(np.loadtxt('diabetes_target.csv.gz',dtype=np.float32))
#自定义多层模型
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear1 = torch.nn.Linear(10,8)
self.linear2 = torch.nn.Linear(8,6)
self.linear3 = torch.nn.Linear(6,4)
self.linear4 = torch.nn.Linear(4,1)
self.sigmoid = torch.nn.Sigmoid() #增加非线性映射
def forward(self,x):
#在多隐层的网络中书写前向计算的逻辑时,只用一个变量x串联整个输入输出
#这是一种习惯
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
x = self.sigmoid(self.linear4(x))
return x
model = Model()
#构建损失函数的计算和优化器
criterion = torch.nn.BCELoss(size_average = True)#逻辑回归模型适用二分类交叉熵损失函数
op = torch.optim.SGD(model.parameters(),lr = 0.1)
epochs = []
costs = []
#训练过程,对每个优化器都进行尝试
for epoch in range(1000):
epochs.append(epoch)
# 前向计算
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
costs.append(loss.item())
print(epoch, loss.item())
# 反向传播
op.zero_grad()
loss.backward()
#权重更新
op.step()
# 训练过程可视化
plt.ylabel('Cost')
plt.xlabel('Epoch')
plt.plot(epochs, costs)
plt.show()
数据集加载
在神经网络训练过程中采用的工具类,诸如
Dataset和DataLoader
Dataset主要用于构造数据集,该数据集应该能够支持索引结构;DataLoader主要用于加载数据集,支持训练时的Mini-Batch形式。
讲述上面的工具类,主要原因是在训练过程的Mini-Batch形式,该形式是介于Batch梯度下降和随机梯度下降之间的一种数据集加载方式,可以较好地兼顾到训练的随机性和时间的效率性。
- 在Mini-Batch模式下,训练过程要写成嵌套循环的形式
for epoch in range(training_epochs):
#对每一个mini-batch进行遍历
for i in range(total_batch):
# do something
- 外层循环控制迭代的次数
- 内层循环控制mini-bacth的索引
- 概念辨析
①Epoch
One forward pass and one backward pass of all the training examples
也即,所有的数据样本都参与了一次训练,就称为是一次Epoch
②Batch-size
The number of training examples in one forward backward pass
也即,每次进行一轮训练时所投入的训练样本的规模
③Iteration
Number of passes,each pass using [batch size]number of examples
通俗来说,就是上面嵌套循环中内层循环执行的次数,iteration=训练样本总数/batch-size
- Dataset构造
①在torch.utils.data中有Dataset抽象类,我们需要根据自己的需要继承这个抽象类,来实现自己的数据集类;
②构造的数据集类中需要实现一些魔术方法:
init:对数据集类进行初始化getitem:对数据集进行索引操作len:对数据集中的数据项个数进行返回③数据集的数据加载方式(
init和getitem的实现)
- 若数据集本身规模不是很大,可以直接将原数据集全部加载到内存中,则
getitem方法只需要从内存中顺序读出即可;- 若数据集本身规模较大,则可以将数据在磁盘中按照文件夹分装,将输入出的各个文件夹名以列表的形式载入内存中;则
getitem的方法就是按照文件夹路径从磁盘中索引并读出文件。
import torch
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
#准备数据,自定义数据集类,用以继承Dataset抽象类
class DiabetesDataset(Dataset):
def __init__(self):
pass
def __getitem__(self, item):
#该方法的实现是为了实例化后的数据集对象支持下标操作
#dataset[index]
pass
def __len__(self):
#该方法的实现是为了方便我们输出数据集每一个batch的数据项条目数
pass
dataset = DiabetesDataset()#实例化这个数据集类
- DataLoader工作机制
①首先DataLoader类需要传入一个支持索引操作的数据集兑现Dataset
②对原始数据集中的各个数据项进行随机打乱操作(Shuffle)
③使用Loader工具,按照给定的Batch-Size大小将原始的数据集划分成以Batch-Size为基本大小的,Batch为基本单位的数据单元
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=2)
'''
dataset:数据集对象
batch_size:批量训练的大小
shuffle:是否要进行随机打乱
num_workers:使用多少个线程对数据进行载入操作;使用并行化可以提高数据读取的效率
'''
- 使用
Dataset和DataLoader进行糖尿病分类
import numpy as np
import torch
from torch.utils.data import Dataset,DataLoader
import matplotlib.pyplot as plt
#准备数据,自定义数据集类,用以继承Dataset抽象类
class DiabetesDataset(Dataset):
def __init__(self):
#xy = np.loadtxt(filepath,delimiter=' ',dtype = np.float32)
self.x_data = torch.from_numpy(np.loadtxt('diabetes_data.csv.gz',delimiter=' ',dtype=np.float32))
self.y_data = torch.from_numpy(np.loadtxt('diabetes_target.csv.gz',dtype=np.float32))
self.len = self.y_data.shape[0]
def __getitem__(self, index):
#该方法的实现是为了实例化后的数据集对象支持下标操作
return self.x_data[index],self.y_data[index]
def __len__(self):
#该方法的实现是为了方便我们输出数据集每一个batch的数据项条目数
return self.len
# x_data = torch.from_numpy(np.loadtxt('diabetes_data.csv.gz',delimiter=' ',dtype=np.float32))
# y_data = torch.from_numpy(np.loadtxt('diabetes_target.csv.gz',dtype=np.float32))
dataset = DiabetesDataset()#实例化这个数据集类
train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True)
'''
dataset:数据集对象
batch_size:批量训练的大小
shuffle:是否要进行随机打乱
num_workers:使用多少个线程对数据进行载入操作;使用并行化可以提高数据读取的效率
'''
#自定义多层模型
class Model(torch.nn.Module):
def __init__(self):
super(Model,self).__init__()
self.linear1 = torch.nn.Linear(10,8)
self.linear2 = torch.nn.Linear(8,6)
self.linear3 = torch.nn.Linear(6,4)
self.linear4 = torch.nn.Linear(4,1)
self.sigmoid = torch.nn.Sigmoid() #增加非线性映射
def forward(self,x):
#在多隐层的网络中书写前向计算的逻辑时,只用一个变量x串联整个输入输出
#这是一种习惯
x = self.sigmoid(self.linear1(x))
x = self.sigmoid(self.linear2(x))
x = self.sigmoid(self.linear3(x))
x = self.sigmoid(self.linear4(x))
return x
model = Model()
#构建损失函数的计算和优化器
criterion = torch.nn.BCELoss(size_average = True)#逻辑回归模型适用二分类交叉熵损失函数
op = torch.optim.SGD(model.parameters(),lr = 0.01)
epochs = []
costs = []
#训练过程,包括前向计算和反向传播
for epoch in range(100):
epochs.append(epoch)
loss_sum = 0.0
for i,data in enumerate(train_loader,0):
inputs,labels = data
#从train_loader中取出数据data
#从数据data中提取属性x和标签y
#并且自动转换成tensor张量传给inputs和data两个变量
y_pred = model(inputs)
loss = criterion(y_pred,labels)
loss_sum += loss.item()
print(epoch,i,loss.item())
op.zero_grad()
loss.backward()
op.step()
costs.append(loss_sum/(i+1))
# 训练过程可视化
plt.ylabel('Cost')
plt.xlabel('Epoch')
plt.plot(epochs, costs)
plt.show()
p.s.P7和P8糖尿病分类的例子,我得到的损失函数值都是很大的负数,而且得到的loss-epoch曲线也很不正常,如果有遇到且解决了这个问题的小伙伴还请说明一下!!
多分类问题
- 多分类的输出处理
- 有m种可能的输出标签,就将最后一层设计成有m个输出,每个输出都表示该数据是其中某一类标签的可能性;
- 为了方便比较,输出的值应该满足某种分布的性质——每个输出值为正;输出值的总和为1;
也就是说,在分类问题中,必须满足输出的每一个值都代表着数据的分布;
p.s.在二分类问题中,经过sigmoid函数后输出一个值,其实就默认满足了分布的性质(p∈(0,1))
- Softmax层的计算
经过上面的分析,我们在多分类问题中得到的输出前加上一个softmax层,就可以满足上方关于输出值的限定。
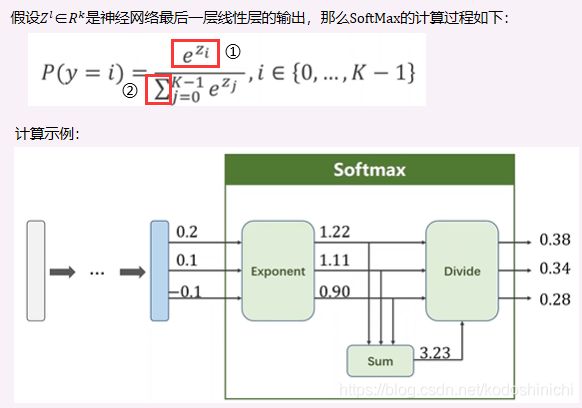
①:将每一个输出值Zi都采用指数幂的运算,保证结果都是正数;
②:分母是每个指数幂结果的求和,保证最后输出的K个结果的总和为1(本质就是归一化操作)。
- 损失函数计算
- 主要思想还是参照二分类中的交叉熵损失函数;但要注意的是交叉熵的计算公式-(ylogy+(1-y)log(1-y))中虽然是有两项,但实际计算中有一项的值恒为零;
- 参照交叉熵的思想,我们对多分类的标签进行独热编码(one-hot),即目标标签值形如[0,0,…0,0,1,0,…,0]这样的稀疏向量;因此损失函数实际为-ylogy

#numpy实现多分类交叉熵损失函数
y = np.array([1,0,0]) #标签值,说明该数据是第1类
z = np.array([0.2,0.1,-0.1]) #神经网络最后一层线性单元的输出值
y_pred = np.exp(z) / np.exp(z).sum() #Softmax层的输出值
loss = (-y * np.log(y_pred)).sum()
#pytorch框架中对多分类损失函数的调用
y = torch.LongTensor([0])
z = torch.Tensor([0.2,0.1,-0.1])
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z,y)
#只需要声明一个损失函数计算对象
#传入标签值和线性单元输出值即可
Exercise9-1:CrossEntropyLoss v.s. NLLLoss
对两类损失函数的完整计算过程的理解可以参考这篇博客《Pytorch详解NLLLoss和CrossEntropyLoss》
①NLLLoss()
torch.nn.NLLLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')
![]()
也就是,损失向量l(x,y)取的是结果矩阵中标签id列所在的计算值;
②EntropyLoss()
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

直观理解交叉熵损失函数的计算过程,就是将得到的神经元输出值,统一进行指数幂的运算,再进行归一化得到概率分布结果,最后对归一化后的结果计算对数值。
利用对数运算的特性,看上图中第二个等式的表示,相当于对于每一个数据样本,log(Σexp(x[j]))都是需要计算的,唯一变化的就是-x[class]——也就是计算结果中和标签id对应的列标处的值。
即:CrossEntropy↔LogSoftMax+NLLLoss
- 案例实现——MNIST手写数字分类
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import matplotlib.pyplot as plt
#准备数据,转换成张量类型的数据,并进行归一化操作
batch_size = 64
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307),(0.3081))
])
train_dataset = datasets.MNIST(root = "../dataset/mnist",
train = True,download=True,transform = transform)
train_loader = DataLoader(train_dataset,shuffle = True,batch_size = batch_size)
test_dataset = datasets.MNIST(root = "../dataset/mnist",train = False,
download=True,transform = transform)
test_loader = DataLoader(test_dataset,shuffle = True,batch_size = batch_size)
#自定义多层模型
class Net(torch.nn.Module):
def __init__(self):
super(Net,self).__init__()
self.linear1 = torch.nn.Linear(784,512)
self.linear2 = torch.nn.Linear(512,256)
self.linear3 = torch.nn.Linear(256,128)
self.linear4 = torch.nn.Linear(128,64)
self.linear5 = torch.nn.Linear(64,10)
def forward(self,x):#使用ReuLU激活单元
x = x.view(-1,784)
x = F.relu(self.linear1(x))
x = F.relu(self.linear2(x))
x = F.relu(self.linear3(x))
x = F.relu(self.linear4(x))
return self.linear5(x)#最后一层线性层的结果直接输出,不再激活
model = Net()
#构建损失函数的计算和优化器
criterion = torch.nn.CrossEntropyLoss()#多分类交叉熵损失函数
op = torch.optim.SGD(model.parameters(),lr = 0.01)#采用SGD
#训练过程,包括前向计算和反向传播,封装成一个函数
def train(epoch):
running_loss = 0.0
for batch_idx,data in enumerate(train_loader,0):
inputs,target = data
op.zero_grad()
#前向计算
outputs = model(inputs)
loss = criterion(outputs,target)
#反向传播与权值更新
loss.backward()
op.step()
running_loss += loss.item()
if batch_idx % 300 == 299:#每训练300代就输出一次
print('[%d,%5d] loss: %3f' % (epoch+1,batch_idx+1,running_loss / 300))
running_loss = 0.0
#测试过程,封装成函数
def vali():
correct = 0
total = 0
with torch.no_grad():#因为test的过程无需反向传播,也就不需要计算梯度
for data in test_loader:
images,labels = data
outputs = model(images)
_,predicted = torch.max(outputs.data,dim = 1)#因为是按批给的数据
#所以得到的数据标签也是一个矩阵
total += labels.size(0) #同样labels也是一个Nx1的张量
correct += (predicted == labels).sum().item()
print('Accuracy on test set: %d %%'%(100 * correct / total))
#主函数逻辑
if __name__ == '__main__':
for epoch in range(10): #一共训练10epochs
train(epoch)
vali()
- 课后作业——ottp电商产品多分类模型
实验过程中比较费力的几个点:
- 多分类交叉熵损失函数计算的本质用到了独热编码的思想,但是在实际调用过程中无需手动将标签值转换成独热编码;
- train.csv文件的标签值是字符串类型,需要转换成数字类型
- 训练过程中的数据类型及其转换要格外注意
import numpy as np
import torch
from torch.utils.data import Dataset,DataLoader
import torch.nn.functional as F
import pandas as pd
#定义数据集
class OttoProduct(Dataset):
def __init__(self):
x = np.loadtxt('../dataset/otto/train.csv',delimiter=',',skiprows = 1,usecols = list(range(1,94)))
self.len = x.shape[0]
self.x_data = torch.from_numpy(x)
y = pd.get_dummies((np.loadtxt('../dataset/otto/train.csv', delimiter=',', dtype = str, skiprows=1,
usecols=94)))#转换成独热编码
self.y_data = torch.from_numpy(np.argmax(y.values,axis = 1))
def __getitem__(self, index):
return self.x_data[index],self.y_data[index]
def __len__(self):
return self.len
dataset = OttoProduct() #实例化数据集
# print(dataset.x_data[:10])
print(dataset.y_data[:10])
train_loader = DataLoader(dataset = dataset,batch_size = 32,shuffle = True)
#定义分类网络结构
class Net(torch.nn.Module):
def __init__(self):
super(Net,self).__init__()
self.l1 = torch.nn.Linear(93,64)
self.l2 = torch.nn.Linear(64,32)
self.l3 = torch.nn.Linear(32,9)
def forward(self,x):
x = x.view(-1,93)
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
return self.l3(x)
model = Net()#实例化网络
#构建损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
op = torch.optim.SGD(model.parameters(),lr = 0.01,momentum = 0.5)
#训练过程
def train(epoch):
running_loss = 0.0
for batch_idx,data in enumerate(train_loader,0):
inputs,target = data
op.zero_grad()
#前向计算
inputs = torch.tensor(inputs,dtype = torch.float32)
outputs = model(inputs)
# print(outputs)
loss = criterion(outputs,target)
#反向传播与权值优化
loss.backward()
op.step()
running_loss += loss.item()
if batch_idx % 500 == 499:#每训练500iterations就打印出结果
print('[%d,%5d] loss: %3f'%(epoch+1,batch_idx+1,running_loss / 500))
running_loss = 0.0
#主函数逻辑
if __name__ == '__main__':
for epoch in range(10):#一共训练10个epochs
train(epoch)