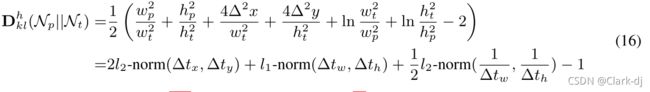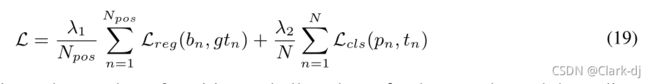【论文阅读】KLD模型

旋转目标检测方法解读（KLD, NeurIPS2021）

旋转目标检测方法解读（KLD, NeurIPS2021） - 知乎

Learning High-Precision Bounding Box for Rotated Object Detection via Kullback-Leibler Diverge

通过Kullback-Leibler Divergence学习旋转目标检测的高精度包围盒

目录

摘要

1 介绍

2 背景

2.1 相关的工作

2.2 损耗设计归纳思维:从特殊视界到一般旋转检测

2.3 损耗设计的演绎思维:从一般旋转到特殊视界检测

 3 提出的方法

4 实验

4.1 数据集和实施细节

4.2 消融研究和进一步比较 

5 结论

简单小结

---

摘要

        现有的旋转目标探测器大多继承了水平探测范式，后者已经发展成为一个成熟的领域。然而，由于现有的回归损耗设计的限制，这些探测器很难在高精度检测中表现突出，特别是对于大纵横比的物体。本文从水平检测是旋转目标检测的特殊情况出发，针对旋转与水平检测的关系，将旋转回归损失的设计从归纳范式改为演绎方法。结果表明，在旋转回归损失中，耦合参数的调制是一个关键的挑战，因为在动态联合优化过程中，估计的参数会以一种自适应和协同的方式相互影响。具体来说，我们首先将旋转的包围盒转换成二维高斯分布，然后计算高斯分布之间的Kullback-Leibler Divergence (KLD)作为回归损失。通过对各参数梯度的分析，表明KLD(及其导数)可以根据物体的特性动态地调整参数梯度。它将根据长宽比调整角度参数的重要性(梯度权重)。这种机制对于高精度检测是至关重要的，因为对于大纵横比的物体，微小的角度误差会导致严重的精度下降。更重要的是，我们已经证明了KLD是尺度不变的。我们进一步证明，KLD损耗可以退化为水平检测的普通范数损耗。在7个数据集上使用不同的检测器进行了实验，结果表明该方法具有一致性的优势，代码可通过http://github.com/yangxue0827/RotationDetection获取。

1 介绍

        旋转目标检测作为航空图像、场景文本等视觉分析的基本组成部分，近年来发展迅速[1,2,3,4,5,6]，受益于成熟的水平检测方法[7,8,9,10,11]。具体来说，许多工作[12,13,14,15]从归纳的角度建立在先前建立的水平盒检测管道上，如图1(a)所示。然而，由于当前回归损失的限制，这些检测器往往不能很好地应对具有挑战性的场景，如物体长径比大、场景密集等，在高精度检测方面存在明显不足。

(a)以往的方法遵循从特殊水平到一般旋转检测的归纳范式。

(b)我们提出的方法采用一般旋转到特殊水平探测的演绎方法。

 图1:以往方法[1,12,13,14,15]与本文方法的水平检测(特殊情况)和旋转检测(一般情况)的方法路线图差异。

        在本文中，我们后退一步，并旨在开发一个统一的回归框架(从演绎的角度)旋转检测及其特殊情况:水平检测。事实上，我们的新框架具有一种相干特性，在特殊情况(水平检测)下，它可以退化为当前常用的回归损失(如ln-范数ln-norm)，如图1(b)所示。 

        在设计高精度旋转检测的旋转回归损失时，一个重要的观察结果是，不同的参数对不同类型的物体的重要性是不同的。例如，角度参数(θ)和中心点参数(x, y)分别对大长宽比物体和小物体很重要。换句话说，推测回归损失在学习过程中应该是自调制的，需要更多的动态优化策略。

        受上述思想的启发，我们首先将旋转的包围盒b (x, y, h, w， θ)转换为二维高斯分布n(µ，Σ)。作为一个标准的距离度量，我们使用Kullback-Leibler Divergence (KLD)[16]来计算预测边界盒与地面真实之间的分布距离作为回归损失。我们将KLD与光滑L1损耗[7]和另一种距离度量高斯Wasserstein distance (GWD)[5,17]进行了比较，发现KLD具有更完整的参数优化机制。特别地，通过分析学习过程中参数的梯度，我们证明了一个参数的优化会受到其他参数(如梯度权值)的影响。这意味着该模型将在给定检测对象的特定配置下自适应调整优化策略，从而在高精度检测中获得优异的性能。此外，KLD被证明是尺度不变的，这是Smooth L1损耗和GWD不具备的重要性质。由于水平包围盒是旋转包围盒的一种特殊情况，我们证明了KLD也可以退化为现有水平检测管道中常用的ln-范数ln-norm损失。本文的亮点有四个方面:

1)与现有的在水平检测器上大量构建旋转检测器的主流做法不同，我们从零开始开发了新的旋转检测损失，并表明在水平检测退化情况下，它与现有的水平检测协议一致。

2)实现一个预测和地面真理之间的原则性更强的测量,而不是计算每个physically-meaningful参数相关的差异在不同的尺度和单位的边界框,我们创新性地将旋转检测的回归损耗转化为两个二维高斯分布的KLD,导致清晰一致的回归损失。

3)通过对KLD中各参数的梯度分析，我们进一步发现KLD的自调制优化机制大大促进了高精度检测的提高，这验证了我们损耗设计的优势。更重要的是，我们已经在理论上证明了(在附录中)KLD对于检测来说是尺度不变的，这对于旋转情况是至关重要的。

4)在七个公共数据集和两个流行的检测器上的大量实验结果表明了我们的方法的有效性，实现了新的最先进的旋转检测性能。

2 背景

首先对水平和旋转目标检测的相关工作进行了概述。然后，我们从两种方法总结了当前的旋转回归损失的设计范式，如图1所示:一是归纳，试图从特殊的、经典的水平检测管道发展出通用的旋转检测。另一种是演绎法，旨在设计一种以水平检测为特例的通用旋转检测管道。

2.1 相关的工作

水平对象检测。水平目标检测涵盖了大多数现有的检测文献，通常使用水平边界框来表示目标。主流的经典目标检测算法大致可以按照以下标准划分:双阶段[7,8,9,11]或单阶段[10,18,19]目标检测，无锚[20,21,22]或基于锚[8,9,10]目标检测，CNN[8,10,20]或基于transformer[23,24]目标检测。尽管管道可能不同，主流的回归损失通常使用流行的标准损失(如平滑L1损失)或基于iou的损失(如GIoU[25]和DIoU[26])。这些检测器也被广泛应用于其他场景，并取得了令人满意的性能。然而，水平探测器不能提供精确的方向和比例信息。

旋转物体检测。旋转检测的最新进展[3,4,12,14,27]主要是由采用旋转包围盒的水平目标检测器来表示多方向目标所驱动的。为了准确预测旋转包围盒，大多数旋转检测方法扩展水平检测中使用的ln-范数ln-norm[12,15,28,29,30]，或构造可微分的近似IoU损失[3,5,31]。我们试图从零开始，将旋转回归损失的设计从归纳范式改为演绎方法论，这实际上是对水平情况的推广。在下面，我们从归纳和演绎的方法来描述现有的工作。

2.2 损耗设计归纳思维:从特殊视界到一般旋转检测

        回归损耗是目前大多数目标检测算法的重要组成部分。对于水平边界盒回归，模型[7,8,9,10,11]主要输出位置和大小四个项:

  (1)

来匹配四个目标的真实情况 

  (2)

其中，y, h, w分别表示中心坐标、高度和宽度。V变量 分别是地面真相箱，锚箱，和预测箱(类似于y, w, h)。 

扩展以上水平情况，现有的旋转检测模型[1,12,13,14,15]也使用了回归损失，只是增加了一个额外的角度参数θ:

 (3) 

其中f(·)用于处理角周期，如三角函数、模等。旋转检测的整体回归损失为: 

 (4) 

 

 

        可以看出，参数是独立优化的，使得任何参数的欠拟合对损失(或检测精度)都很敏感。这种机制对高精度检测是致命的。以图2左侧为例，基于平滑L1损耗的检测结果往往显示中心点或角度的偏移。此外，不同类型的物体对这五个参数的敏感性也不同。例如，角度参数对于检测大纵横比的物体非常重要。这就要求在训练过程中为特定的单个对象样本选择一组合适的权重，这是非常重要的，甚至是不现实的。 

图2:平滑L1损耗(左)、GWD(中)和KLD(右)的视觉对比。  

2.3 损耗设计的演绎思维:从一般旋转到特殊视界检测

        为了打破原有的归纳设计范式，我们采用演绎范式来构造更精确的旋转回归损失。在这里，我们重新表述最近的工作[5]的主要思想，该工作将一个任意方向的包围盒 (x, y, h, w， θ)转换为一个二维高斯(µ，Σ)，如图3所示。然后计算两个高斯函数之间的距离作为最终损耗。具体来说，转换为: 

其中为旋转矩阵，为特征值对角矩阵。

最近的工作[5]分析了(µ，Σ)的引入可以解决度量与损耗不一致、边界不连续和类方问题。在此基础上，进一步研究了如何利用新的参数空间设计高精度的检测回归损耗。我们的观点是，自调制机制与最终的高精度性能呈正相关。 

 高斯瓦瑟斯坦距离Gaussian Wasserstein Distance.。两个概率度量之间的瓦瑟斯坦距离[5,17]表示为:

 (6)

        由式6可知，高斯瓦瑟斯坦距离(GWD)主要分为两部分:中心点(x, y)距离与围绕杆θ的耦合项之间的距离。因此，基于GWD的回归损耗可以看作是一种半耦合损耗。虽然由于部分参数之间的耦合，GWD可以大大提高高精度旋转检测的性能，但由于中心点的独立优化，使得检测结果略有偏移(见图2)。需要注意的是，GWD不是比例不变的，这不是检测友好性的。 

当所有盒子都水平时(θ= 0◦)，则式6可进一步简化:

                                                                                                                                                       (7)

        是Frobenius规范。虽然Eq. 7仍然可以作为水平检测的回归损失，但是Eq. 4和7并不是完全一致的。GWD方案虽然对演绎范式进行了初步的探索，但并不注重实现高精度检测和尺度不变性。下面，我们将基于Kullback-Leibler divergence (KLD)[16]提出我们的新方法。 

 3 提出的方法

为了探究更合适的回归损失，我们采用Kullback-Leibler Divergence (KLD)[16]。同样，两个二维高斯函数之间的KLD为:

  （8）

或者

   （9）

        可以看出，的每一项都是由部分参数耦合组成的，这使得所有参数形成了链式耦合关系。在基于KLD的检测器的优化过程中，各参数相互影响，共同优化，使得模型的优化机制是自调制的。相比之下，和GWD都是半耦合的，但具有更好的中心点优化机制。

        虽然KLD是不对称的，但通过分析各参数的梯度和实验结果，我们发现这两种形式的优化原则是相似的。以比较简单的为例，根据Eq. 5, Eq. 8中的每一项都可以表示为

  （10）

  （11）

  （12）

高精度检测分析Analysis of high-precision detection。在不失一般性的前提下，设= 0◦，则 

 （13）

和将使模型根据尺度动态调整物体的最佳位置。例如，当对象规模较小或边缘过短时，模型就会更加关注相应方向偏移的优化。对于这类对象，在相应方向上的轻微偏差往往会导致IoU急剧下降。当θt不等于 0◦时，对象偏移的梯度(∆x和∆y)将根据θ t进行动态调整，以获得更好的优化。而GWD和L2范数中中心点的梯度是和前者不能根据对象的长度和宽度来调整动态梯度，后者是基于锚的长度和宽度()来调整梯度而不是目标对象()，这对于那些使用水平锚进行旋转检测的检测器[3,13,15,27,28,32,33]几乎无效。更重要的是，它们与目标物体的角度无关。因此，基于GWD模型和Ln-norm模型的检测结果会有轻微偏差，而基于KLD模型的检测结果比较准确，如图2所示。 

对于hp和wp,我们有

一方面，hp和wp的优化受到以下因素的影响：∆θ. 

当∆θ= 0◦, ，这意味着目标高度或宽度越小，其匹配损失的惩罚越重。这是可取的，因为较小的高度或宽度需要更高的匹配精度。

另一方面，优化∆θ也受hp和wp的影响：

ht=wt时，这表明对象的纵横比越大，模型将更加关注角度的优化。这就是基于KLD的模型在高精度检测指标方面具有巨大优势的主要原因，因为对于大宽高比的对象，微小的角度误差会导致严重的精度下降。通过以上分析，我们发现当其中一个参数被优化时，其他参数将作为其权重来动态调整优化率。换言之，参数的优化不再是独立的，即优化一个参数也会促进其他参数的优化。这种良性循环的优化是KLD作为优秀旋转回归损失的关键。此外 具有类似的特性，详情请参阅附录。

尺度不变性。（略，矩阵证明）关于满秩矩阵M,，我们有，其中 。因此，可以证明KLD的仿射不变性（包括M=kI时的尺度不变性，其中I单位矩阵）（见附录中的证明）。与Ln范数和GWD相比，KLD由于与检测度量的一致性，更适合代替不可微旋转IoU损失。

水平特例。（公式证明）对于水平检测，结合等式8到等式12，我们得到

式中，公式16的前两项与公式4非常相似，两项的除数部分x和y是主要区别 

KLD的变体。我们还引入了KLD的一些变体[34,35]，以进一步验证不对称性对旋转检测的影响可以忽略。这些变体主要包括

 旋转回归损失。探测器的整个训练过程如下：

1. i）预测偏移量；
2. ii）解码预测框；
3. iii）将预测框和目标地面真值转换为高斯分布；
4. iv）计算两个高斯分布的KLD。

因此，推断时间保持不变。我们将距离函数标准化为最终回归损失： 

 式中，f（·）表示一个非线性函数，用于变换距离D以使损失更平滑、更具表现力。在本文中，我们主要使用两个非线性函数，。超参数调制整个损耗。多任务损失为：

 式中，和N表示正锚和所有锚的数量。bn表示第n个边界框，gtn表示第n目标地面真相。tn表示第n个对象的标签，pn是由sigmoid函数计算出的各种类别的概率分布。超参数λ1、λ2控制折衷，默认设置为{2,1}。分类损失被设置为focal loss 焦点损失[10]。

此部分感觉是从数学性质方面验证。 

4 实验

4.1 数据集和实施细节

        我们的实验是在各种数据集上进行的，包括三个大型航空图像公共数据集DOTA[36]、UCAS-AOD[37]、HRSC2016[38]以及场景文本数据集ICDAR2015[39]、MLT[40]和MSRA-TD500[41]。

DOTA 是航空图像中最大的面向对象检测数据集之一，发布了三个版本：DOTA-v1.0，DOTA-v1.5和DOTA-v2.0。DOTA-v1.0包含15个常见类别、2806个图像和188282个实例。DOTA-v1.0中训练集、验证集和测试集的比例分别为1/2、1/6和1/3。相反，DOTA-v1.5使用与DOTA-v1相同的图像。但也会注释非常小的实例（小于10像素）。此外，此版本中添加了一个新类别，共包含402089个实例。而DOTA-v2.0包含18个常见类别、11268个图像和1793658个实例。与DOTA-v1.5相比，它进一步包括新的类别。DOTA-v2.0中的11268个图像分为培训、验证、测试开发和测试挑战集。我们将图像划分为600×600子图像，重叠150像素，并将其缩放到800×800，这与文献[5,27]中的裁剪协议一致。

UCAS-AOD 包含约659×1280像素的1510幅航空图像，共有两类14596个实例。根据[30,36]，我们随机选择1110进行培训，400进行测试。HRSC2016包含两个场景的图像，包括海上船舶和近海船舶。训练、验证和测试集包括436、181和444幅图像。

ICDAR2015、MLT和MSRA-TD500通常用于定向场景文本检测和定位。ICDAR2015包括1000张培训图像和500张测试图像。ICDAR2017 MLT是一个多语言文本数据集，包括7200个培训图像、1800个验证图像和9000个测试图像。MSRA-TD500数据集由300个训练图像和200个测试图像组成。

我们使用Tensorflow[42]在一台带有Tesla V100和32G内存的服务器上实现了所提出的方法。除非另有规定，否则默认情况下，所有实验均由ResNet50[43]初始化。权重衰减和动量分别设置为0.0001和0.9。我们使用超过8个GPU的MomentumOptimizer，每个小批量总共有8个图像（每个GPU 1个图像）。

所有使用的数据集总共经过20个阶段的训练，学习率在12个阶段和16个阶段分别降低10倍。初始学习速率设置为5e-4。DOTA-v1.0、DOTA-v1.5，DOTA-v2.0、UCAS-AOD、HRSC2016、ICDAR2015、MLT和MSRA-TD500每个历元的图像迭代次数分别为54k、64k、80k、5k、10k、10k、10k、10k、10k和5k，如果使用数据增强（包括随机旋转、翻转和灰度化）或多尺度训练，则增加一倍。

论文错误吧？ 

4.2 消融研究和进一步比较 

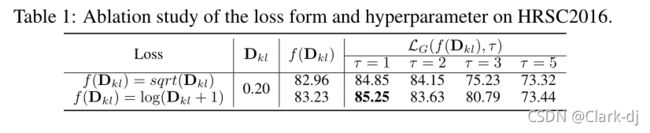
回归损失形式和超参数。（介绍实验分析略）

表1:HRSC2016损失形式和超参数的消融研究。

 表2：基于KLD的不同回归损失形式的消融。基于 RetinaNet的探测器。

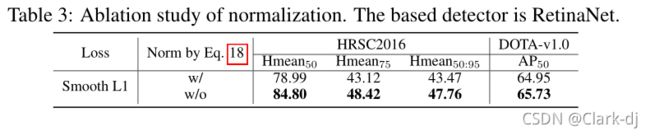
标准化的消融研究。如上所述，使用公式18是为了平滑其过快的增长趋势，并发挥正常化作用。这个额外的规范化问题是KLD是否真的在结果中起作用，还是仅仅在结果中产生噪声。为了进一步证明我们的方法确实有效，我们还对平滑的L1损失进行了归一化操作，以消除归一化引起的干扰。如表3所示，使用规范化后，性能显著下降。上述实验结果证明，KLD的有效性并非来自公式18。 

表3：标准化的消融研究。基于RetinaNet 的探测器。

高精度检测实验。我们期望所设计的旋转回归损耗在高精度检测中显示出优势。表4显示了在不同数据集和不同检测器上使用平滑L1、GWD和KLD对三种不同回归损失的高精度检测结果的比较。对于包含大量宽高比船舶的HRSC2016数据集，与AP75上的平滑L1相比，基于GWD的RetinaNet具有11.89%的提高，KLD甚至获得了23.97%的增长。即使有更强的R3Det探测器，KLD和GWD仍然增加了33.96%和22.46%AP75，在AP50:95，为15.22%和9.89%。同样的实验结论也反映在另外两个场景文本数据集MASR-TF500和ICDAR2015中，即KLD>GWD>Smooth L1。一般来说，自调制优化机制对高精度检测有很大帮助。为了进行更直观的比较，我们直观地比较了这三种回归损失，如图2所示。由于平滑L1损耗和GWD中的中心点（x，y）参数是独立优化的，因此它们的预测结果略有偏移。相比之下，基于KLD的预测结果更接近对象边界，在密集场景中表现出较强的鲁棒性。类似地，基于GWD或KLD的模型比基于平滑L1的模型具有更精确的角度预测能力，因为它们的角度参数（θ）没有独立优化。

表4：不同回归损失下的高精度检测实验R、F和G分别表示随机旋转、翻转和灰显。
HRSC2016、MSRA-TD500和ICDAR2015的分辨率分别为500×500800×1000和800×1000。

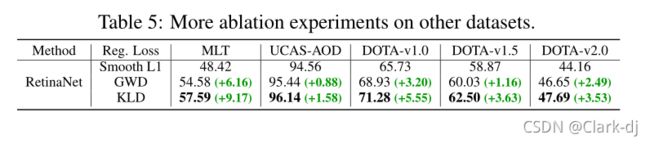
更多数据集的消融研究。为了使结果更加可信，我们继续对其他五个数据集进行验证，如表5所示。在MLT、UCAS-AOD和DOTA-v1.0三个数据集上改进KLD仍然相当可观，分别增加了9.17%,1. 58%和5.55%。请注意，对于DOTA-v1.5和DOTA-v2.0，其中包含大量的小对象（小于10个像素），KLD已经获得了3.63%和3.53%的显著增益。

表5：其他数据集的更多消融实验。

对等方法的比较。表6比较了六种对等技术，包括DOTA-v1.0上的IoU平滑L1损耗[3]、调制损耗[44]、RIL[33]、CSL[4,46]、DCL[45]和GWD[5]。为了公平起见，这些方法都在相同的基线方法上实现，并且在相同的环境和超参数下进行训练和测试。我们详细说明了七个类别的准确性， 包括大纵横比（如BR、SV、LV、SH、HA）和方形物体（如ST、RD），能够更好地反映我们方法的现实挑战和优势。RetinaNet和KLD的组合直接超过R3Det（AP50: 71.28%vs70.66%，7-AP50: 69.41%vs68.31%）。即使与R3Det相结合，KLD仍能进一步提高大纵横比目标（7-AP50为2.82%）和高精度检测（AP75为6.07%，AP50:95为3.65%）的性能。基于KLD的方法在几乎所有指标中表现最好。在更具挑战性的数据集（DOTA-v1.5和DOTA-v2.0）上仍然可以得出类似的结论，这些数据集包含更多数据和微小对象（小于10像素）。

表6:DOTA数据集上不同旋转检测器之间的精度比较。
†和‡分别表示大纵横比对象和方形对象。粗体和蓝色字体分别表示前两名的表现。
doc和dle表示OpenCV定义（θ∈[−90◦,0◦))和长边定义（θ∈[−90◦,90◦))是RBox的。

水平检测验证。如等式16所分析，KLD可退化为水平检测任务中常见的回归损失。表7比较了水平检测的回归损失平滑L1和IoU/GIoU与MS COCO[47]数据集上建议的回归损失KLD。结果表明，在更快的RCNN[8]、RetinaNet[10]和FCOS[20]上，我们的KLD并不比其他损失差，RetinaNet甚至有0.6%的改进。旋转检测的地面真值是最小外接矩形，这意味着地面真值能够很好地反映物体的真实尺度和方向信息。本文所描述的“水平特例”也满足上述要求，此时水平外切矩形等于最小外切矩形。虽然COCO的基本事实是一个水平长方体，但它不是最小外接矩形，这意味着它丢失了对象的方向信息和精确的比例信息。例如，倾斜放置在图像中的棒球棒，其水平外接矩形的高度和宽度并不表示对象本身的高度和宽度。这导致当KLD应用于COCO时，KLD根据纵横比动态调整角度梯度的优化机制毫无意义，从而影响最终性能的提高。一般来说，这是数据集注释本身的一个缺陷，而不是KLD不够好。事实上，用COCO来讨论θ=0◦是不合适的, 因为COCO丢弃了θ参数。此外，θ=0◦描述处于水平位置的实例，但并不意味着数据集的所有实例都处于水平位置。本文使用COCO讨论“水平特例”来表示，即使数据集有一定的标记缺陷，KLD也可以产生一定的效果。毕竟，很难观察旋转数据集上所有水平对象的性能改进。 

5 结论

局限性。尽管有理论基础和有前景的实验证明，我们的方法有一个明显的局限性，不能直接应用于四边形检测[33,44]。

潜在的负面社会影响。我们的发现为高精度旋转检测提供了一个简单的回归损失。然而，我们的研究可能会应用到一些敏感领域，如遥感、航空和无人机。

结论。本文从现有的大量目标检测文献出发，从零开始设计了一种新的旋转检测回归损失算法，并将流行的水平检测作为其特例。具体地，我们计算旋转包围盒对应的高斯分布之间的KLD作为回归损失，我们发现在KLD损失指导的学习过程中，参数的梯度可以根据目标的特性动态调整，这是鲁棒目标检测所需要的特性，无论其旋转、大小和宽高比等。我们还证明了KLD具有尺度不变性，这对检测任务至关重要。有趣的是，我们已经证明，在水平检测任务中，KLD可以退化为目前常用的ln-范数ln-norm损失。在不同探测器和数据集上的大量实验结果表明了我们方法的有效性。

简单小结

• 之前：从水平检测归纳旋转检测。
• 现在：从旋转检测归纳水平检测。

 具体改进：

1. 将旋转的包围盒(x, y, h, w， θ)转换成二维高斯分布(µ，Σ)
2. 计算高斯分布之间的Kullback-Leibler Divergence (KLD)作为回归损失

优势：

1. 本身性质： 通过对各参数梯度的分析，表明KLD(及其导数)可以根据物体的特性动态地调整参数梯度。
   （任务本身有这种需求：不同的参数对不同类型的物体的重要性是不同的（不同类型的物体对这五个参数的敏感性也不同。）。例如，角度参数(θ)和中心点参数(x, y)分别对大长宽比物体和小物体很重要。
   重要性：这种机制对于高精度检测是至关重要的，因为对于大纵横比的物体，微小的角度误差会导致严重的精度下降。）
2. KLD是尺度不变的。

与其他损失函数的关系 ：

1. KLD损失可以退化为水平检测的普通范数损失。
2. 平滑L1损失不足：基于平滑L1损失的检测结果往往显示中心点或角度的偏移。
3. GWD：部分耦合，中心点的独立优化：高斯瓦瑟斯坦距离(GWD)主要分为两部分:中心点(x, y)距离与围绕杆θ的耦合项之间的距离。因此，基于GWD的回归损失可以看作是一种半耦合损失。
   优：部分参数之间的耦合-----》GWD可以大大提高高精度旋转检测的性能；
   不足：由于中心点的独立优化-----》使得检测结果略有偏移(见图2)。
   需要注意的是，GWD不是比例不变的，这不是检测友好性的。 
4. KLD：
   1）每一项都是由部分参数耦合组成的，这使得所有参数形成了链式耦合关系。在基于KLD的检测器的优化过程中，各参数相互影响，共同优化，使得模型的优化机制是自调制的。
   2）相比之下，和GWD都是半耦合的，但具有更好的中心点优化机制。
   3）KLD是不对称的，但通过分析各参数的梯度和实验结果，我们发现这两种形式的优化原则是相似的。
   （论文通过公式分析了为什么GWD 和L2-norm会偏移，KLD不会偏移）
    

 旋转回归损失。探测器的整个训练过程如下：

1. i）预测偏移量；
2. ii）解码预测框；
3. iii）将预测框和目标地面真值转换为高斯分布；
4. iv）计算两个高斯分布的KLD。

数学论证、消融实验很充分 （理论本质+实验验证）