Supervised Contrastive Learning:有监督对比学习
1 概要
交叉熵损失是监督学习中应用最广泛的损失函数,度量两个分布(标签分布和经验回归分布)之间的KL散度,但是也存在对于有噪声的标签缺乏鲁棒性、可能存在差裕度(允许有余地的余度)导致泛化性能下降的问题。而大多数替代方案还不能很好地用于像ImageNet这样的大规模数据集。
许多对正则交叉熵的改进实际上是通过对loss定义的放宽进行的,特别是参考分布是轴对称的。这写改进通常具有不同的动机:比如标签平滑(Label smoothing)通过偏离轴来模糊区分正确和不正确的标签,从而在许多应用中提供了很小但是很重要的提升;在自蒸馏中,利用前几轮的“软”标签作为参考类分布进行多轮交叉熵训练;混合和相关数据增强策略通常通过线性插值创建明确的、新的训练示例,然后将相同的线性插值应用于目标标签分布,类似于软化原始交叉熵loss。用这些修改方法训练的模型显示了改进的泛化、鲁棒性和校准。
本文提出了一个新的loss,受对比loss与度量学习启发,完全去除参考分布,而只是将来自相同类的规范化嵌入强行加在一起,使得其比来自不同类的嵌入更加紧密。
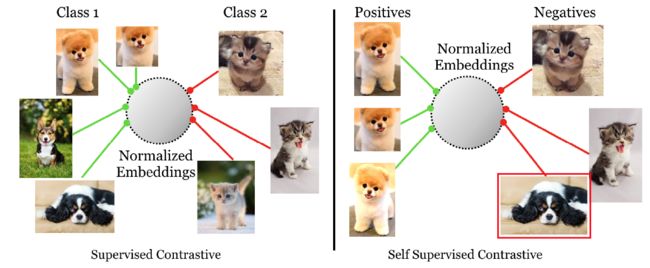
具体来说,在对比学习中,核心思想是拉近某一个锚点与其正样本之间的距离,拉远锚点与该锚点其他负样本之间的距离,通常来说,一个锚点只有一个正样本,其他全视为负样本。而本文的方法认为每个锚点有许多的正样本,而不是许多负样本,并且通过标签显示样本之间的正负关联。比如下面的图,右侧是典型的对比学习方法,通常将一张原图通过数据增强得到两个子样本,这一对子样本之间构成一对正对,而与其他数据的子样本构成负对;而本文的有监督对比学习中,每个子样本可能都有很多的正对和负对。
本文构造的loss在ResNet50和ResNet200上都取得了不错的Top-1效果,在自动增强的ResNet50上取得78。8%的Top-1精度,比同样数据增强下的交叉熵loss提升了1.6%,不仅如此,还更鲁棒。
具体的Contribution如下:
- 我们提出了一个新的扩展对比损失函数,允许每个锚点有多个正对。因此,我们将对比学习适应于完全监督的设置。
- 我们表明,与交叉熵相比,这种损失使我们能够了解最先进的表示方式,从而显著提高了Top-1的准确性和鲁棒性。
- 我们的损失对超参数范围的敏感性不如交叉熵。这是一个重要的实际考虑。我们相信,这是由于我们的损失使用更自然的公式,使从同一类样本的代表被拉得更近,而不是像交叉熵一样强迫他们被拉向一个特定的目标。
- 我们分析地表明,我们的损失函数的梯度鼓励从hard positive和hard negative中学习。我们还表明,三联体损失是我们损失只有一个正极和负极被使用的一个特例。
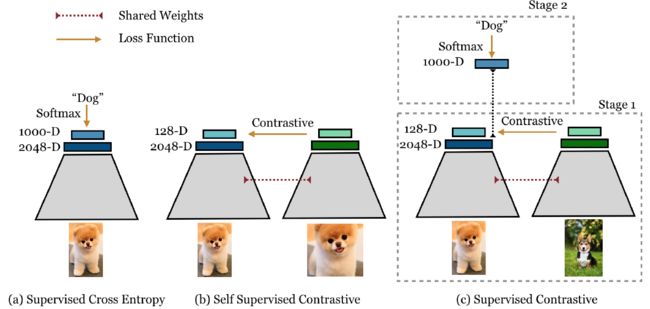
具体来说,有监督对比学习的框架是交叉熵loss和传统对比学习的结合:
2 具体结构
2.1 表征学习框架
总的来说,有监督对比学习框架的结构类似于表征学习框架,由如下几个部分组成:
-
数据增强模块
数据增强模块 A ( ⋅ ) A(·) A(⋅)的作用是将输入图像转换为随机增强的图像 x ~ \widetilde{x} x ,对每张图像都生成两张增强的子图像,代表原始数据的不同视图。数据增强分为两个阶段:第一阶段是对数据进行随机裁剪,然后将其调整为原分辨率大小;第二阶段使用了三种不同的增强方法,具体包括:(1)自动增强,(2)随机增强,(3)Sim增强(按照顺序进行随机颜色失真和高斯模糊,并可能在序列最后进行额外的稀疏图像扭曲操作)。
-
编码器网络
编码器网络 E ( ⋅ ) E(·) E(⋅)的作用是将增强后的图像 x ~ \widetilde{x} x 映射到表征空间,每对子图像输入到同一个编码器中得到一对表征向量,本文用的是ResNet50和ResNet200,最后使用池化层得到一个2048维的表征向量。表征层使用单位超球面进行正则化。
-
投影网络
投影网络 P ( ⋅ ) P(·) P(⋅)的作用是将表征向量映射成一个最终向量 z z z进行loss的计算,本文用的是只有一个隐藏层的多层感知器,输出维度为128。同样使用单位超球面进行正则化。在训练完成后,这个网络会被一个单一线性层取代。
2.2 对比损失
本文的数据是带有标签的,采用mini batch的方法获取数据,首先从数据中随机采样 N N N个样本对,记为 { x k , y k } k = 1 , 2 , . . . , N \left\{ {x}_k,{y}_k\right\}_{k=1,2,...,N} {xk,yk}k=1,2,...,N, y k {y}_k yk是 x k {x}_k xk的标签,之后进行数据增强获得 2 N 2N 2N个数据样本 { x ~ k , y ~ k } k = 1 , 2 , . . . , 2 N \left\{\widetilde{x}_k,\widetilde{y}_k\right\}_{k=1,2,...,2N} {x k,y k}k=1,2,...,2N,其中, x ~ 2 k \widetilde{x}_{2k} x 2k和 x ~ 2 k − 1 \widetilde{x}_{2k-1} x 2k−1是分别用两种随机增强方法得到的数据对,在数据增强过程中,标签信息始终不会改变。
2.2.1 自监督对比损失
本文的自监督对比损失与SimCLR的loss相类似,不过使用的是点积刻画样本之间的相似性,具体表达式如下:
L s e l f = ∑ i = 1 2 N L i s e l f L i s e l f = − log exp ( z i ⋅ z j ( i ) / τ ) ∑ k = 1 2 N l [ k ≠ i ] ⋅ exp ( z i ⋅ z j ( i ) / τ ) \mathcal{L}^{self}=\sum_{i=1}^{2N}{\mathcal{L}_{i}^{self} }\\ \mathcal{L}_{i}^{self}=-\log\frac{\exp(z_i·z_{j(i) }/\tau) } {\sum_{k=1}^{2N} {\mathbb{l}_{ [k{\neq}i] }·\exp(z_i·z_{j(i) }/\tau) } } Lself=i=1∑2NLiselfLiself=−log∑k=12Nl[k=i]⋅exp(zi⋅zj(i)/τ)exp(zi⋅zj(i)/τ)
上式中, l [ k ≠ i ] \mathbb{l}_{ [k{\neq}i] } l[k=i]是一个指示函数,当且仅当 k = i k=i k=i时取0,否则为1。 τ \tau τ是进行优化的温度参数。该loss的意义在于拉近 x ~ i \widetilde{x}_i x i于其正对 x ~ j ( i ) \widetilde{x}_{j(i)} x j(i)之间的距离而拉远 x ~ i \widetilde{x}_i x i与其他负对之间的距离。
2.2.2 有监督的对比损失
有监督对比损失是对自监督对比损失的推广,从公式中很容易可以看出,有监督对比损失拓展了 x ~ i \widetilde{x}_i x i正对的数量,将所有标签信息相同的子数据都视为正对,计算了 x ~ i \widetilde{x}_i x i与其所有正对之间的相似性,之后进行加权平均。
L s u p = ∑ i = 1 2 N L i s u p L i s u p = − 1 2 N y ~ i − 1 ∑ j = 1 2 N l [ i ≠ j ] ⋅ l [ y ~ i = y ~ j ] ⋅ log exp ( z i ⋅ z j ( i ) / τ ) ∑ k = 1 2 N l [ k ≠ i ] ⋅ exp ( z i ⋅ z j ( i ) / τ ) \mathcal{L}^{sup}=\sum_{i=1}^{2N} {\mathcal{L}_{i}^{sup} }\\ \mathcal{L}_{i}^{sup}=\frac{-1} {2N_{\widetilde{y}_i}-1}\sum_{j=1}^{2N} {\mathbb{l}_{ [i{\neq}j] }·\mathbb{l}_{ [ {\widetilde{y}_i}={\widetilde{y}_j} ] } }·\log\frac{\exp(z_i·z_{j(i)}/\tau)}{\sum_{k=1}^{2N}{\mathbb{l}_{ [k{\neq}i] }·\exp(z_i·z_{j(i)}/\tau)} } Lsup=i=1∑2NLisupLisup=2Ny i−1−1j=1∑2Nl[i=j]⋅l[y i=y j]⋅log∑k=12Nl[k=i]⋅exp(zi⋅zj(i)/τ)exp(zi⋅zj(i)/τ)
作者指出对比损失的核心是足够多的负对,以便与正对形成鲜明的对比,他们的改进监督对比损失保留了这一特性。此外,由于增加了正对的数量,这一架构还可以更好地刻画类内相似性。
2.2.3 有监督对比损失的梯度特性
这一部分论证了hard positive和hard negative更有助于提升网络的性能,主要是通过对有监督对比损失的梯度进行分析,在此略去。
此外,作者在论文中还论述了三联loss是他们的有监督对比损失的特例,此处省略不讲。
3 实验
作者在评估其框架性能时,使用了Top-1精度和对损坏图像的鲁棒性两个方面进行衡量,还评价了其模型对超参数的稳定性以及正对数量对模型表现的影响。在实现上,使用的是训练好的网络,之后将网络的非线性投影头替换成一个简单的线性全连接层,使用标准交叉熵损失训练这个线性层。网络的训练在ImageNet上进行。
3.1 ImageNet分类精度
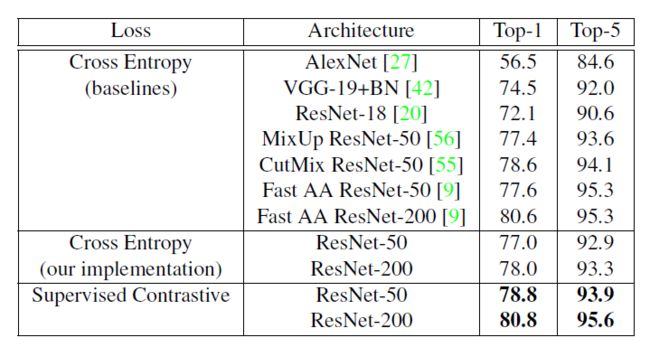
这部分实验比较了他们的方法与其他使用交叉熵的有监督方法的Top-1与Top-5精度,同时对比了他们的架构使用交叉熵损失的表现,可以看到,综合来说他们的方法实现了最好的效果,同时,他们的架构在使用交叉熵损失时的表现就不是非常好,相对来说,他们的架构在改进loss的情况下,Top-1精度提升了3.8/2.8个点,Top-5精度提升了1/2.3个点。
3.2 对图像损坏和校准的鲁棒性
这部分实验评价了他们的方法对图像扰动的稳定性,具体来说,他们选择使用对ImageNet数据库中的图像应用常见的自然扰动,比如加噪声、模糊和对比度变化,构造得到的ImageNet-c数据集进行测试。使用平均损坏误差与平均相对损坏误差作为评价指标,可以看到,他们的方法的误差最小,且使用改进的对比损失替换交叉熵损失也有助于提升网络的性能。

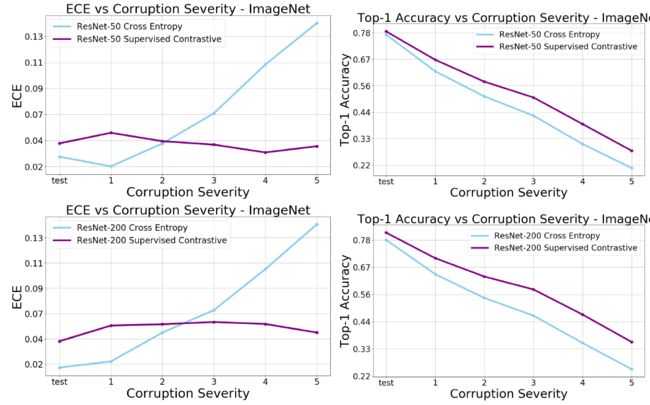
此外,和交叉熵损失相比,本文的对比损失在不同程度的图像损坏下都能保持一个相对稳定的平均损失误差,相比于交叉熵损失也有更高的Top-1精度:
3.3 对超参数的鲁棒性
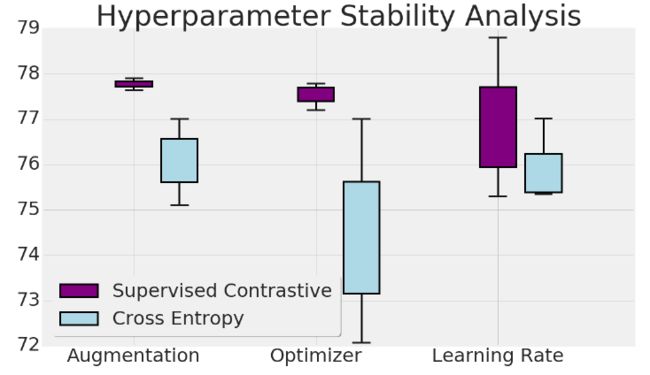
通常深度网络对超参数都很敏感,本文还比较了他们的改进对比损失对不同优化器、不同数据增强和学习率的分类精度稳定性。三种增强方式是本文提出的三种;优化器则选用了LARS、带动量的SGD和RMSProp;选择了最佳学习率以及增大或减小十倍的三个学习率进行评估,可以发现,本文提出的loss确实和交叉熵损失相比,对这三种超参数的变化更鲁棒。
3.4 不同正对数量对模型表现的影响
作者对比了每个子数据有1、2、3、5个正对时的Top-1精度,发现正对越多越有助于提升模型表现,当然同时计算成本也更大。
