FGFCM图像分割实现
FGFCM算法基本原理
由于传统FCM算法不考虑图像上下文中的任何信息,仅凭借像素值对应的最大隶属度所在类对该像素点进行分类,这使得它对噪声十分敏感。
为了克服这一缺陷,FGFCM算法引入了局部空间关系与局部灰度关系,通过对某一像素值邻域中的像素自动赋予权重以此更新该点的像素值,从而消除或减弱局部噪声的影响。
其权值计算方式如下:
上式通过计算邻域内灰度值的标准差来量化这一邻域内像素分布的离散程度,以此作为参数带入下式:
这里计算邻域像素对应权值时主要考虑两点:
- 局部空间关系:邻域内像素所处的环与中心像素的距离,主要体现出距离该像素越近的像素灰度值对其加权和的权值越大
- 局部灰度关系:邻域各像素值与中心灰度值的平方差作为基准,加入标准差影响
得到邻域权重之后,通过带权平均法得到该点处新的像素值:
将原图像的灰度值用新的加权平均灰度值替换后可得到原图像的线性加权图,新的图像弱化了噪声带来的局部影响,在此基础上进行FCM图像分割,其结果优于直接进行FCM。
python实现
import cv2
import numpy as np
from math import *
import matplotlib.pyplot as plt
def gauss_noise(image, mean=0, var=0.005):
'''
添加高斯噪声
mean : 均值
var : 方差
'''
image = np.array(image / 255, dtype=float)
noise = np.random.normal(mean, var ** 0.5, image.shape)
out = image + noise
if out.min() < 0:
low_clip = -1.
else:
low_clip = 0.
out = np.clip(out, low_clip, 1.0)
out = np.uint8(out * 255)
return out
class FgFcm:
def __init__(self, img, v_num):
self.img = img
self.img_noise = gauss_noise(img) # 得到含有高斯噪声的图像
self.hist = cv2.calcHist([self.img_noise], [0], None, [256], [0, 256]) # 计算直方图
self.new_img = self.img_noise
self.v_num = v_num # 聚类数目
self.cluster_ = None
self.v = []
for i in range(v_num): # 初始化聚类中心
self.v.append(np.random.randint(0, 256))
self.flag = True
def img_process(self, nearby, lambda_s, lambda_g): # 计算线性加权图
blank = int((nearby - 1) / 2) # 空白处理
expansion_img = np.zeros([self.img_noise.shape[0] + nearby - 1, self.img_noise.shape[1] + nearby - 1]) # 填充
[x, y] = expansion_img.shape
img_new = np.zeros(expansion_img.shape)
expansion_img[blank:x - blank, blank:y - blank] = self.img_noise
for r in range(blank, expansion_img.shape[0] - blank):
for c in range(blank, expansion_img.shape[1] - blank):
sigma = 0 # 计算邻域灰度值标准差
for i in range(r - blank, r + blank + 1):
for j in range(c - blank, c + blank + 1):
sigma += (expansion_img[i, j] - expansion_img[r, c]) ** 2
sigma /= (nearby ** 2 - 1)
s_ = 0 # 累计加权和
s__ = 0 # 累计权值和
for i in range(r - blank, r + blank + 1):
for j in range(c - blank, c + blank + 1):
if i == r and j == c: # 判断邻域中心
S = 0
else:
if sigma: # 处理标准差为零的情况
S = exp(-(max(abs(r - i), abs(c - j)) / lambda_s +
(expansion_img[r, c] - expansion_img[i, j]) ** 2 / (lambda_g * sigma)))
else:
S = exp(-(max(abs(r - i), abs(c - j)) / lambda_s))
s_ += S * expansion_img[i, j]
s__ += S # 累计权值
if s__: # 处理权值和为零的情况
img_new[r, c] = s_ / s__
else:
img_new[r, c] = expansion_img[r, c]
self.new_img = img_new.astype(np.uint8)
self.hist = cv2.calcHist([self.new_img], [0], None, [256], [0, 256])
def cal_U(self, m, hist):
U = np.zeros([256, self.v_num])
l = np.array([x for x in range(256)])
for i in range(len(hist)): # 遍历每一个像素值
for k in range(self.v_num): # 遍历聚类中心
s = 0
for r in range(self.v_num): # 计算累加
s += pow(((l[i] + 0.00001 - self.v[k]) / (l[i] + 0.00001 - self.v[r])), (2 / (m - 1)))
U[i, k] = 1 / s
return U
def cal_V(self, m, hist):
v_new = np.zeros(len(self.v))
U = self.cal_U(m, hist) # 计算出隶属度矩阵
l = np.array([x for x in range(256)])
for i in range(self.v_num):
numerator = 0
denominator = 0
for j in range(256): # 计算新聚类中心
numerator += hist[j] * pow(U[j, i], m) * l[j] # 分子累计
denominator += hist[j] * pow(U[j, i], m) # 分母
v_new[i] = int(numerator / denominator) # 第i个聚类中心
# 计算两次聚类中心欧式距离判断是否迭代结束
s = 0
for i in range(self.v_num):
s += (self.v[i] - v_new[i]) ** 2
s = sqrt(s)
if s < 0.00001:
self.flag = False
self.v = v_new
def cluster(self, m):
while self.flag:
self.cal_V(m, self.hist) # 更新聚类中心
U = self.cal_U(m, self.hist) # 计算最终隶属度
hist = self.hist
for i in range(256):
u = U[i]
index_ = np.where(u == max(u)) # 最大隶属度原则映射灰度值
hist[i] = self.v.astype(np.uint8)[index_[0][0]]
img_cluster = np.zeros(self.new_img.shape)
for i in range(256):
img_cluster[self.new_img == i] = hist[i] # 图像灰度值映射
self.cluster_ = img_cluster
file_path = ""
img = cv2.imread(r"file_path", 0)
c = 4 # 聚类数目
fcm = FgFcm(img, c)
fcm.img_process(3, 3, 6)
fcm.cluster(m=2)
# 直接FCM结果
fcm2 = FgFcm(img, c)
fcm2.cluster(m=2)
FCM = fcm2.cluster_
plt.figure()
plt.rcParams['font.sans-serif'] = ['SimHei'] # 防止中文乱码
plt.subplot(2, 2, 1)
plt.imshow(img, cmap='gray')
plt.title("(a)原图")
plt.subplot(2, 2, 2)
plt.imshow(fcm.img_noise, cmap='gray')
plt.title("(b)高斯含噪图")
plt.subplot(2, 2, 3)
plt.imshow(FCM, cmap='gray')
plt.title("(c)FCM")
plt.subplot(2, 2, 4)
plt.imshow(fcm.cluster_, cmap='gray')
plt.title("(d)FGFCM")
plt.tight_layout()
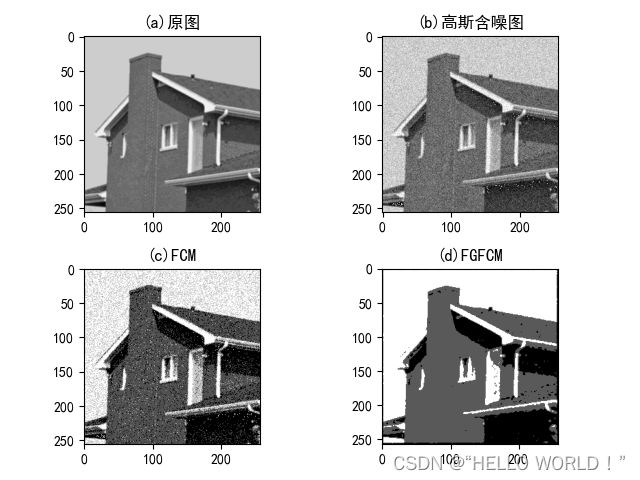
plt.show()效果比对:
(本文仅为实验过程记录,不作其他用途)
参考文献:Weiling Cai, Songcan Chen, Daoqiang Zhang. Fast and robust fuzzy c-means clustering algorithms incorporating local information for image segmentation. Pattern Recognition, 2007, 40(3): 825-838.