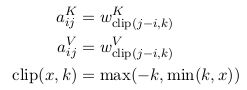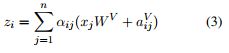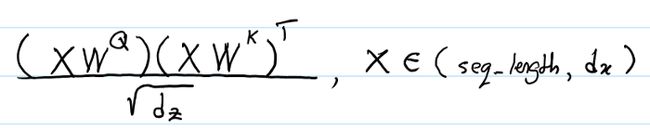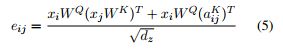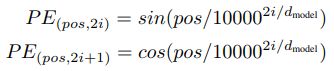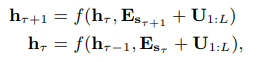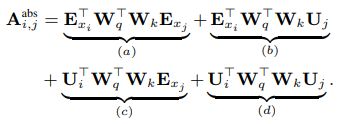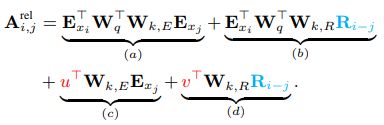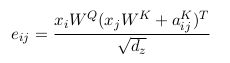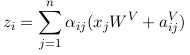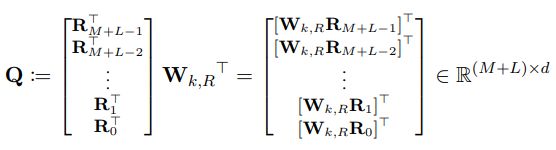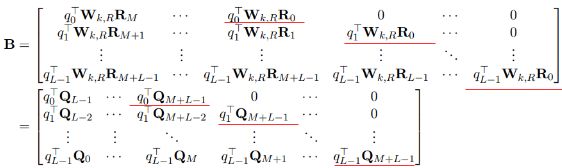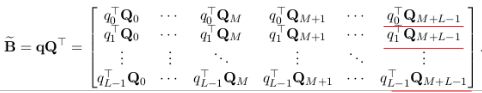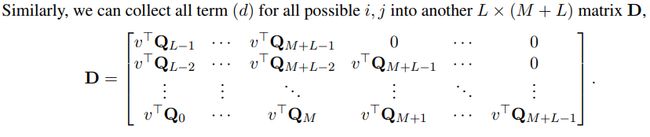Relative Positional Encodings

参考：

https://www.cnblogs.com/shiyublog/p/11185625.html

https://www.cnblogs.com/shiyublog/p/11236212.html

第一部分

目录

• Motivation
• 概述
• 符号含义 
• 实现
• 高效实现
• 结果

 

---

对于Transformer模型的positional encoding，最初在Attention is all you need的文章中提出的是进行绝对位置编码，之后Shaw在2018年的文章中提出了相对位置编码，就是本篇blog所介绍的算法RPR；2019年的Transformer-XL针对其segment的特定，引入了全局偏置信息，改进了相对位置编码的算法，在相对位置编码(二)的blog中介绍。 

本文参考链接：

1. Self-Attention with Relative Position Representations (Shaw et al.2018): https://arxiv.org/pdf/1803.02155.pdf 

2. Attention is all you need (Vaswani et al.2017): https://arxiv.org/pdf/1706.03762.pdf

3. How Self-Attention with Relative Position Representations works: https://medium.com/@_init_/how-self-attention-with-relative-position-representations-works-28173b8c245a

4. [NLP] 相对位置编码(二) Relative Positional Encodings - Transformer-XL: https://www.cnblogs.com/shiyublog/p/11236212.html

Top

Motivation

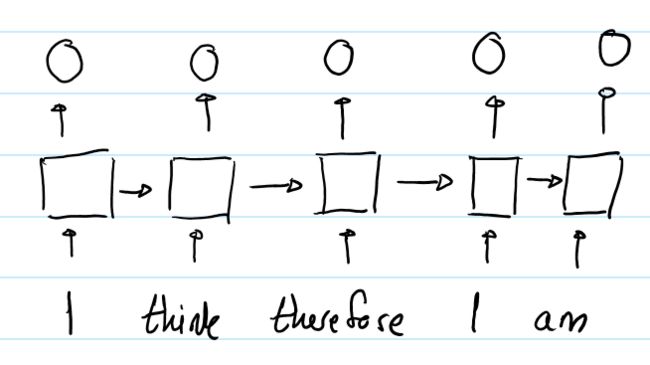
RNN中，第一个"I"与第二个"I"的输出表征不同，因为用于生成这两个单词的hidden states是不同的。对于第一个"I"，其hidden state是初始化的状态；对于第二个"I"，其hidden state是编码了"I think therefore"的hidden state。所以RNN的hidden state 保证了在同一个输入序列中，不同位置的同样的单词的output representation是不同的。

在self-attention中，第一个"I"与第二个"I"的输出将完全相同。因为它们用于产生输出的“input”是完全相同的。即在同一个输入序列中，不同位置的相同的单词的output representation完全相同，这样就不能提现单词之间的时序关系。--所以要对单词的时序位置进行编码表征。

Top

概述

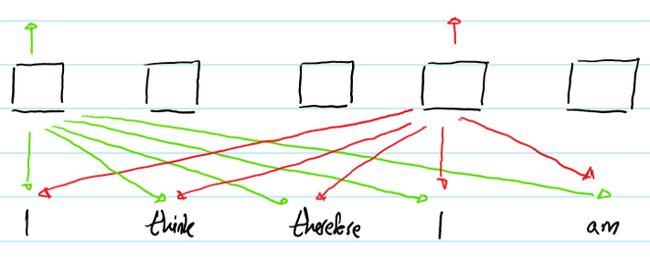
作者提出了在Transformer模型中加入可训练的embedding编码，使得output representatino可以表征inputs的时序信息。这些embedding vectors是 在计算输入序列中的任意两个单词i,ji,j 之间的attention weight 和 value时被加入到其中。embedding vector用于表示单词i,ji,j之间的距离(即为间隔的单词数),所以命名为"相对位置表征" (Relative Position Representation) (RPR)

比如一个长度为5的序列，需要学习9个embeddings。(1个表示当前单词，4个表示其左边的单词，4个表示其右边的单词。)

以下例子展示了这些embeddings的用法:

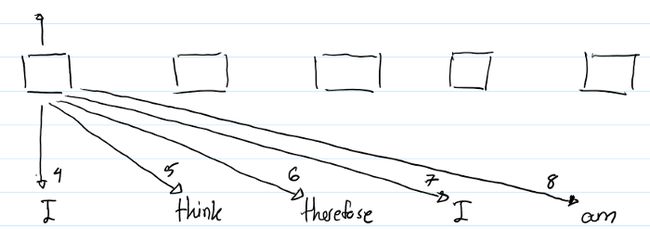
1) 

以上图示显示了计算第一个"I"的output representation的过程。箭头下面的数字显示了计算attention时用到的哪个RPRs.(比如，本示例是求第一个“I”的输出，需要用第一个“I”,记为''I_1'，与sequence中每一个单词两两做self-attention运算。'I_1' with 'I_1'用到 index = 4 的RPR，“I_1”with 'think'用到index = 5 的RPR--因为是右边第一个， 'I_1' with 'therefore' 用到index = 6的RPR--因为是右边第二个... )

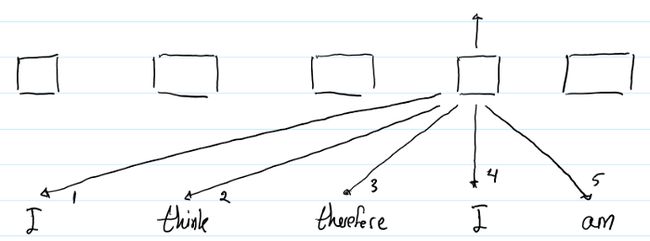
2)  

与(1)同理。

Top

符号含义 

两点需要注意：

1. 有2个RPR的表征。需要在计算zizi和eijeij时分别引入对应的RPR的embedding。计算zizi时对应的RPR vector 是aVijaijV, 计算eij时引入的RPRvectoreij时引入的RPRvector是aKijaijK. 不同于在做multi-head attention时引入的线性映射矩阵W——对于每个head都不同；这个RPR embedding 在同一层的attention heads之间共享，但是在不同层的RPR可能不同。

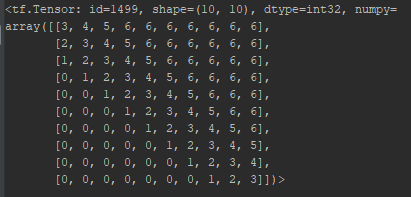
2. 最大单词数被clipped在一个绝对的值k以内。向左k个, 再左边均为0， 向右k个，再右边均为k, 所表示的index范围： 2k + 1. 

eg. 10 words, k = 3, RPR embedding lookup table 

设置k值截断的意义：

1. 作者假设精确的相对位置编码在超出了一定距离之后是没有必要的

2. 截断最大距离使得模型的泛化效果好，可以更好的Generalize到没有在训练阶段出现过的序列长度上。

之后，将分别学习key, value的相对位置表征。

 

wK=(wK−k,...,wKk),wV=(wV−k,...,wVk)wK=(w−kK,...,wkK),wV=(w−kV,...,wkV)

其中wKi,wVi∈RdawiK,wiV∈Rda.

Top

实现

1. 若不使用RPR, 计算zizi的过程：

 

2. 若使用RPR，计算zizi的过程：

(3) 表示在计算word i 的output representation时，对于word j的value vector进行了修改，加上了word i, j 之间的相对位置编码。

(4) 在计算query(i), key(j)的点积时，对key vector进行了修改，加上了word i, j 之间的相对位置编码。

这里用加法引入RPR的信息，是一种高效的实现方式。

Top

高效实现

不加RPR时，Transformer计算eijeij使用了 batch_size * h 个并行的矩阵乘法运算。

其中的x是给定input sequence后的(row-wise)

将(4) 式写为以下形式：

(1) 首先看第一项，

xiWQ(xjWK)TxiWQ(xjWK)T

首先看对于一个batch,的一个head， 其中xixi的shape是(seq_length, dx)，现在假设seq_length = 1,来简化推导过程。假设WQ,WKWQ,WK的shape均为(dx, dz)，那么第一项运算后的shape为：[(1 * dx) * (dx, dz)] * [(dz, dx) * (dx, 1)] = (1, 1)，

这是对于一个batch,一个head, seq_length = 1的情况，那么扩充到真实的情况，其shape 为： (batch_size, h, seq_length, seq_length)

所以我们的目标是产生另一个有相同shape的tensor，其内容是word i 与关于Wordi, j 的RPR的embedding的点积。

(2) A.shape: (seq_length, seq_length, d_a)，

transpose→AT.shape:transpose→AT.shape:(seq_length, d_a, seq_length)

(3) 第二项中的xiWQ.shape:xiWQ.shape: (batch_size, h, seq_length, d_z)

transpose→transpose→ (seq_length, batch_size, h, d_z)

reshape→reshape→ (seq_length, batch_size * h, d_z)

之后可以与ATAT相乘，可以看做是seq_length个并行的(batch_size * h, d_z) matmul (d_a, seq_length)，因为dz=dadz=da，所以每个并行的运算结果是：(batch_size * h, seq_length), 总的大矩阵的shape: (seq_length, batchsize * h, seq_length).

reshape→reshape→(seq_length, batch_size, h, seq_length)

transpose→transpose→ (batch_size, h, seq_length, seq_length)

与第一项的shape一致，可以相加。

(3)式的推导同理。

下面给出tensor2tensor中对于相对位置编码的代码：https://github.com/tensorflow/tensor2tensor/blob/9e0a894034d8090892c238df1bd9bd3180c2b9a3/tensor2tensor/layers/common_attention.py#L1556-L1587

其中x,对应上面推导中的xi∗WQxi∗WQ, y对应上面推导中的xj∗WKxj∗WK, z对应上面的a。

 1 def _relative_attention_inner(x, y, z, transpose):
 2   """Relative position-aware dot-product attention inner calculation.
 3   This batches matrix multiply calculations to avoid unnecessary broadcasting.
 4   Args:
 5     x: Tensor with shape [batch_size, heads, length or 1, length or depth].
 6     y: Tensor with shape [batch_size, heads, length or 1, depth].
 7     z: Tensor with shape [length or 1, length, depth].
 8     transpose: Whether to transpose inner matrices of y and z. Should be true if
 9         last dimension of x is depth, not length.
10   Returns:
11     A Tensor with shape [batch_size, heads, length, length or depth].
12   """
13   batch_size = tf.shape(x)[0]
14   heads = x.get_shape().as_list()[1]
15   length = tf.shape(x)[2]
16 
17   # xy_matmul is [batch_size, heads, length or 1, length or depth]
18   xy_matmul = tf.matmul(x, y, transpose_b=transpose)
19   # x_t is [length or 1, batch_size, heads, length or depth]
20   x_t = tf.transpose(x, [2, 0, 1, 3])
21   # x_t_r is [length or 1, batch_size * heads, length or depth]
22   x_t_r = tf.reshape(x_t, [length, heads * batch_size, -1])
23   # x_tz_matmul is [length or 1, batch_size * heads, length or depth]
24   x_tz_matmul = tf.matmul(x_t_r, z, transpose_b=transpose)
25   # x_tz_matmul_r is [length or 1, batch_size, heads, length or depth]
26   x_tz_matmul_r = tf.reshape(x_tz_matmul, [length, batch_size, heads, -1])
27   # x_tz_matmul_r_t is [batch_size, heads, length or 1, length or depth]
28   x_tz_matmul_r_t = tf.transpose(x_tz_matmul_r, [1, 2, 0, 3])
29   return xy_matmul + x_tz_matmul_r_t

Top

结果

使用Attention is All You Need的机器翻译的任务。在training steos每秒去掉7%的条件下，模型的BLEU分数对于English-to-German最高提升了1.3, 对于English-to-French最高提升了0.5.

第二部分

目录

• 1. Motivation
• 2. Relative Positional Encodings
  • vanilla Transformer中的绝对位置编码
• 3. Transformer-XL中的相对位置编码
  • 改进1) Uj→Ri−jUj→Ri−j.
  • 改进2)  (c):UTiWTq→u∈Rd(c):UiTWqT→u∈Rd；(d):UTiWTq→v∈Rd(d):UiTWqT→v∈Rd
  • 改进3) Wk→Wk,EWk→Wk,E, Wk,RWk,R
  • 与shaw的RPR的对比
  • 优势：
• 4. 高效计算方法
• 5. 总结

 

---

Top

1. Motivation

在Transformer-XL中，由于设计了segments，如果仍采用transformer模型中的绝对位置编码的话，将不能区分处不同segments内同样相对位置的词的先后顺序。

比如对于segmentisegmenti的第k个token，和segmentjsegmentj的第k个token的绝对位置编码是完全相同的。

鉴于这样的问题，transformer-XL中采用了相对位置编码。

Top

2. Relative Positional Encodings

paper中，由对绝对位置编码变换推导出新的相对位置编码方式。

vanilla Transformer中的绝对位置编码

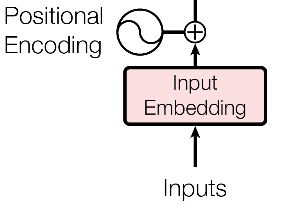
它对每个index的token都通过sin/cos变换，为其唯一指定了一个位置编码。该位置编码将与input的embedding求sum之后作为transformer的input。

那么如果将该位置编码应用在transformer-xl会怎样呢？

其中ττ表示第ττ个segment, 是当前segment的序列sτsτ的word embedding sequence, LL是序列长，dd是每个word embedding的维度。U1:LU1:L表示该segment中每个token的绝对位置编码组成的序列。

可以看到对于hτ+1hτ+1和hτhτ，其在位置编码表示是完全相同的，都是U1:LU1:L,这样就会造成motivation中所述的无法区分在不同segments中相对位置相同的tokens.

Top

3. Transformer-XL中的相对位置编码

transformer-xl中没有采用vanilla transformer中的将位置编码静态地与embedding结合的方式；而是沿用了shaw et al.2018的相对位置编码中通过将位置信息注入到求Attention score的过程中，即将相对位置信息编码入hidden state中。

为什么要这么做呢？paper中给出的解释是：

1) 位置编码在概念上讲，是为模型提供了时间线索或者说是关于如何收集信息的"bias"。出于同样的目的，除了可以在初始的embedding中加入这样的统计上的bias, 也可以在计算每层的Attention score时加入同样的信息。

2) 以相对而非绝对的方式定义时间偏差更为直观和通用。比如对于一个query vector qτ,iqτ,i 与 key vectors kτ,≤ikτ,≤i做attention时，这个query 并不需要知道每一个key vector在序列中的绝对的位置来决定segment的时序。它只需要知道每一对kτ,jkτ,j 和其本身qτ,iqτ,i的相对距离(比如，i - j)就足够。

因此，在实际中可以创建一个相对位置编码的encodings矩阵 R∈RLmax×dR∈RLmax×d，其中第i行 RiRi表示两个pos(比如位置pos_q, pos_k)之间的相对距离为i. (可以参考我在参考链接3中的介绍，以下图示便是一个简单的说明例子.

但是图示中的i表示query的位置pos, 与RiRi 中的i不同。如果以该图示为例，当pos_q = i, pos_k = i - 4时， 相对位置为 0, 二者的相对位置编码是 R0R0。

--------------------------------------------------------------------------------------------------

Transformer-XL的相对位置编码方式是对Shaw et al.,2018 和 Huang et al.2018提出模型的改进。它由采用绝对编码计算Attention score的表达式出发，进行了改进3项改变。

若采用绝对位置编码，hidden state的表达式为：

，

那么对应的query,key的attention score表达式为：

(应用乘法分配率， query的embedding 分别与 key的embedding, positional encoding相乘相加；之后 query的positional encoding分别与 key的embedding, positional encoding相乘相加)

(其中i是query的位置index，j是key的位置index) (WE, WU是对embedding进行linear projection的表示，细节内容可以参看attention is all you need 中对multi-head attention的介绍)

，

Transformer-XL 对上式进行了改进：

改进1) Uj→Ri−jUj→Ri−j.

首先将 Aabsi,jAi,jabs 中的key vector的绝对位置编码 UjUj 替换为了相对位置编码 Ri−jRi−j 其中 RR是一个没有需要学习的参数的sinusoid encoding matrix，如同Vaswani et al., 2017提出的一样。

该改进既可以避免不同segments之间由于tokens在各自segment的index相同而产生的时序冲突的问题。

改进2)  (c):UTiWTq→u∈Rd(c):UiTWqT→u∈Rd；(d):UTiWTq→v∈Rd(d):UiTWqT→v∈Rd

在改进1中将key的绝对位置编码转换为相对位置编码，在改进2中则对query的绝对位置编码进行了替换。因为无论query在序列中的绝对位置如何，其相对于自身的相对位置都是一样的。这说明attention bias的计算与query在序列中的绝对位置无关，应当保持不变. 所以这里将Aabsi,jAi,jabs 中的c,d项中的UTiWTqUiTWqT分别用一个可学习参数u∈Rdu∈Rd,v∈Rdv∈Rd替换。

改进3) Wk→Wk,EWk→Wk,E, Wk,RWk,R

在vanilla transformer模型中，对query, key分别进行线性映射时，query 对应WqWq矩阵，key对应WkWk矩阵，由于input 是 embedding 与 positional encoding的相加，也就相当于

queryembeddingWq+queryposencodingWqqueryembeddingWq+queryposencodingWq得到query的线性映射后的表征；

keyembeddingWq+keyposencodingWqkeyembeddingWq+keyposencodingWq 得到key的线性映射后的表征。

可以看出，在vanilla transformer中对于embedding和positional encoding都是采用的同样的线性变换。

在改进3中，则将key的embedding和positional encoding 分别采用了不同的线性变换。其中Wk,EWk,E对应于key的embedding线性映射矩阵，Wk,RWk,R对应与key的positional encoding的线性映射矩阵。

在这样的参数化定义后，每一项都有了一个直观上的表征含义，(a)表示基于内容content的表征，(b)表示基于content的位置偏置，(c)表示全局的content的偏置,(d)表示全局的位置偏置。

与shaw的RPR的对比

shaw的RPR可以参考我在参考链接3中的介绍。这里给出论文中的表达式：其中ai,jai,j是query i, key j的相对位置编码矩阵AA中的对应编码。

attention score: (在key的表征中加入相对位置信息)

softmax计算权值系数：

attention score * (value + 的output：(在value的表征中加入相对位置信息)

1) 对于eijeij可以用乘法分配率拆解来看，那么其相当于transforerm-xl中的(a)(b)两项。也就是在shaw的模型中未考虑加入(c)(d)项的全局内容偏置和全局位置偏置。

2) 还是拆解eijeij来看，涉及到一项为xiWQ(aKij)TxiWQ(aijK)T，是直接用 query的线性映射后的表征 与 相对位置编码相乘；而在transformer-xl中，则是与query的线性映射后的表征 与 相对位置编码也进行线性映射后的表征 相乘。

优势：

paper中指出，shaw et al用单一的相对位置编码矩阵 与 transformer-xl中的WkRWkR相比，丢失掉了在原始的 sinusoid positional encoding (Vaswani et al., 2017)中的归纳偏置。而XL中的这种表征方式则可以更好地利用sinusoid 的inductive bias。

----------------------------为什么XL中的这种表征方式则可以更好地利用sinusoid 的inductive bias？--------------------------------------------------------------------

有几个问题：原始的 sinusoid positional encoding (Vaswani et al., 2017)中的归纳偏置是什么呢？为什么shaw et al 把它丢失了呢？为什么transformer-xl可以适用呢？

这里需要搞清楚：

1. 为什么在vanilla transformer中使用sinusoid？

2. shaw et al.2018中的相对位置编码Tensor是什么？

3. transformer-xl的相对位置编码矩阵是什么？

对于1，sinusoid函数具有并不受限于序列长度仍可以较好表示位置信息的特点。

We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training. ~Attention is all you need.

为什么不用学得参数而采用sinusoid函数呢？sinusoidal函数并不受限于序列长度，其可以在遇到训练集中未出现过的序列长度时仍能很好的“extrapolate.” (外推)，这体现了其具有一些inductive bias。

对于2，shaw et al.2018中的相对位置编码Tensor是两个需要参数学习的tensor. 

相对位置编码矩阵是设定长度为 2K + 1的(K是窗口大小) ,维度为dada的2个tensor(分别对应与key的RPR和value的RPR)，其第i行表示相对距离为i的query,key(或是query, value)的相对位置编码。这两个tensor的参数都是需要训练学习的。那么显然其是受限于最大长度的。在RPR中规定了截断的窗口大小，在遇到超出窗口大小的情况时，由于直接被截断而可能丢失信息。

对于3，transformer-xl的相对位置编码矩阵是一个sinusoid矩阵，不需要参数学习。

在transformer-xl中虽然也是引入了相对位置编码矩阵，但是这个矩阵不同于shaw et al.2018。该矩阵Ri,jRi,j是一个sinusoid encoding 的矩阵(sinusoid 是借鉴的vanilla transformer中的)，不涉及参数的学习。

具体实现可以参看代码，这里展示了pytorch版本的位置编码的代码：

 1 class PositionalEmbedding(nn.Module):
 2     def __init__(self, demb):
 3         super(PositionalEmbedding, self).__init__()
 4 
 5         self.demb = demb
 6 
 7         inv_freq = 1 / (10000 ** (torch.arange(0.0, demb, 2.0) / demb))
 8         self.register_buffer('inv_freq', inv_freq)
 9 
10     def forward(self, pos_seq, bsz=None):
11         sinusoid_inp = torch.ger(pos_seq, self.inv_freq)
12         pos_emb = torch.cat([sinusoid_inp.sin(), sinusoid_inp.cos()], dim=-1)
13 
14         if bsz is not None:
15             return pos_emb[:,None,:].expand(-1, bsz, -1)
16         else:
17             return pos_emb[:,None,:]

其中dembdemb是embedding的维度。

sinusoid的shape：[batch_size, seq_length × (d_emb / 2)]

sin,cos concat之后，pos_emb的shape：[batch_size, seq_length × d_emb]

pos_emb[:,None,:]之后的shape：[batch_size, 1, seq_length × d_emb]

---

那么综合起来看，transformer-xl的模型的hidden states表达式为：

Top

4. 高效计算方法

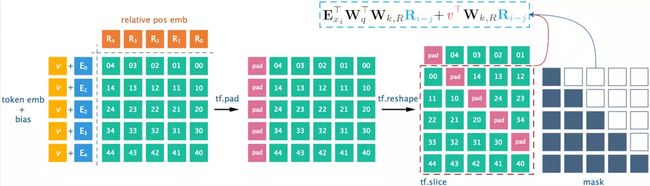
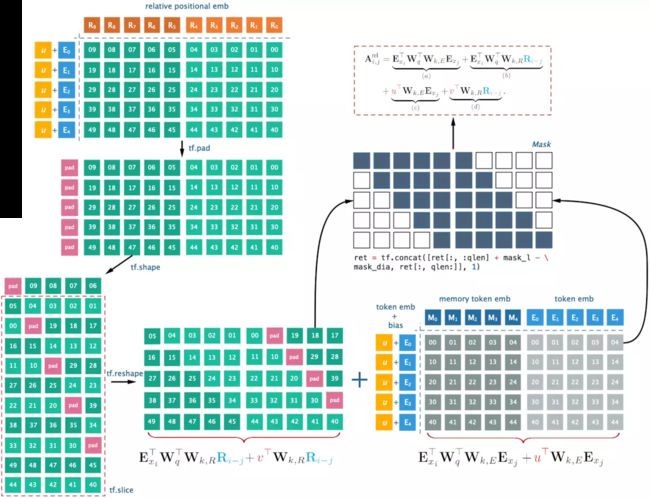
在该表达式中，在计算Wk,RRi−jWk,RRi−j时，需要对每一对(i,j)进行计算，时间复杂度是O(n2)O(n2)。paper中提出了高效的计算方法，使其降为O(n).O(n).

核心算法：发现(b)项组成的矩阵的行列之间的关系，构建一个矩阵，将其按行左移，恰好是(b)项矩阵BB，而所构建的矩阵只需要O(n)O(n)时间。

由于相对距离(i-j)的变化范围是[0, M + L - 1] (其中M是memory的长度，L是当前segment的长度)

那么令：

那么将(b)项应用与所有的(i,j)可得一个L×(M+L)L×(M+L)的矩阵 BB: (其中q是对E经过WqWq映射变换后的表示)

看这些带红线的部分，是不是只有q的下标不一样！

如果我们定义B˜B~:

对比BB与B˜B~发现，将B˜B~的第i行左移 L−1−iL−1−i个单位即为BB。而B˜B~的计算仅涉及到两个矩阵的相乘，因此BB的计算也仅需要求qQTqQT之后按行左移即可得到，时间复杂度降为O(n)O(n)!

同理，可以求(d)项的矩阵D。

 

这样将B，D原本需要O(n2)O(n2)的复杂度，降为了O(n)O(n).

 

 

 

 

Top

5. 总结

Transformer-XL针对其需要对segment中相对位置的token加入位置信息的特点，将vanilla transformer中的绝对位置编码方式，改进为相对位置编码。改进中涉及到位置编码矩阵的替换、query全局向量替换、以及为key的相对位置编码和embedding分别采用了不同的线性映射矩阵W。

transformer-xl与shaw et al.2018的相对编码方式亦有区别。1. shaw et al.2018的相对编码矩阵是一个需要学习参数的tensor,受限于相对距离的窗口长度设置；而transformer-xl的相对编码矩阵是一个无需参数学习的使用sinusoid表示的矩阵，可以更好的generalize到训练集中未出现长度的长序列中；2. 相比与shaw et al.2018，transformer-xl的attention score中引入了基于content的bias，和基于位置的bias。

另外在计算优化上，transformer-xl提出了一种高效计算(b)(d)矩阵运算的方法。通过构造可以在O(n)O(n)时间内计算的新矩阵，并将其项左移构建出目标矩阵B，D的计算方式，将时间复杂度由O(n2)O(n2)降为O(n)O(n)。

 

参考：

1. Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context: https://arxiv.org/pdf/1901.02860.pdf

2. Self-Attention with Relative Position Representations (shaw et al.2018): https://arxiv.org/pdf/1803.02155.pdf

3. [NLP] 相对位置编码(一) Relative Position Representatitons (RPR) - Transformer https://www.cnblogs.com/shiyublog/p/11185625.html