机器学习-使用决策树DecisionTreeClassifier()对鸢尾花数据集进行分类

1．1决策树回归的工作基础

主要任务是首先介绍什么时决策树和信息增益，平均误差，Gini系数等一些基础概念，之后手动推演和上机实践实现决策树的分类与回归

1．2决策树分类的实验条件

使用了python作为主要工具。

1．3 设计思想

使用基尼系数作为划分标准，基尼系数越小，则不纯度越低，区分的越彻底。
假设一个数据集中有K个类别，第K个类别的概率为pk,则基尼系数表达式为：

对于个给定的样本D，假设有K个类别，第k个类别的数量为CkCk,则样本D的基尼系数表达式为:

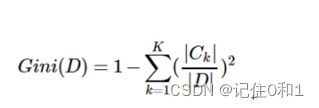
1．4运行结果及分析

首先，通过键盘交互式按键“T”，开始训练；训练集和测试集按4：1进行划分，前四份用于训练，后一份用于测试，并用混淆矩阵来评判分类后的结果。
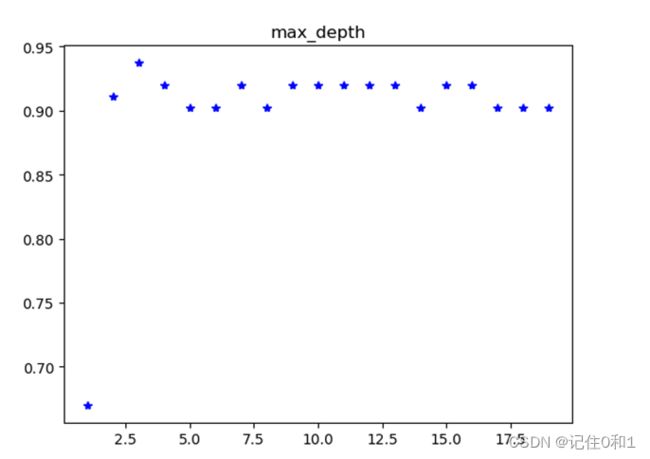
通过掉用封装好的决策树API接口，默认的参数虽然是最优的担并不适用于任何数据集，不用的需求也相应着模型的参数不同。通过网格搜索交叉验证的方式来寻找模型的最优参数，以下为对max_depth；min_samples_split ；min_samples_leaf 这三个参数进行调优。
注：①max_depth（树的最大深度）：默认为None，此时决策树在建立子树的时候不会限制子树的深度。也可以设置具体的整数，一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布

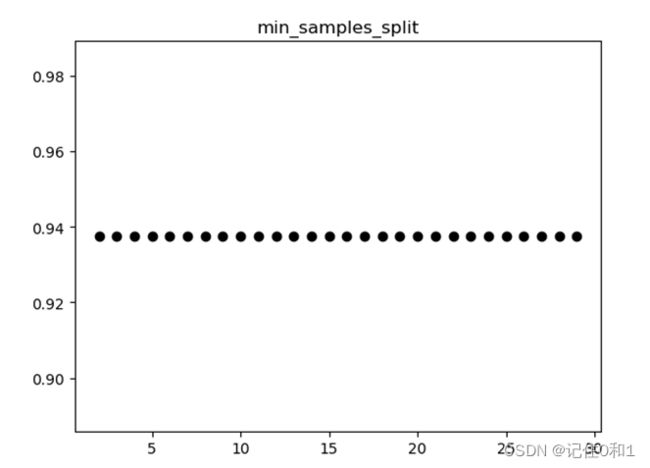
②min_samples_split（分割内部节点所需的最小样本数）：意思就是只要在某个结点里有k个以上的样本，这个节点才需要继续划分，这个参数的默认值为2，也就是说只要有2个以上的样本被划分在一个节点，如果这两个样本还可以细分，这个节点就会继续细分

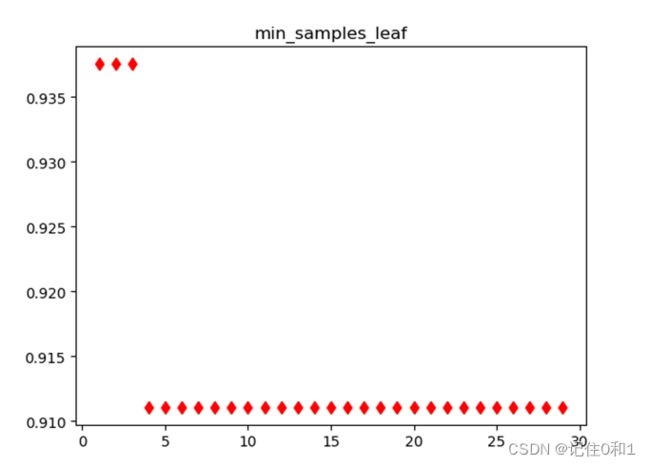
③min_samples_leaf（叶子节点上的最小样本数）：当你划分给某个叶子节点的样本少于设定的个数时，这个叶子节点会被剪枝，这样可以去除一些明显异常的噪声数据。默认为1，也就是说只有有两个样本类别不一样，就会继续划分。

交叉验证后得出的是模型最后的得分结果，我们选择最大深度为3，此刻得分最高。同时在最优深度的条件下进行对分割内部节点数进行调优。

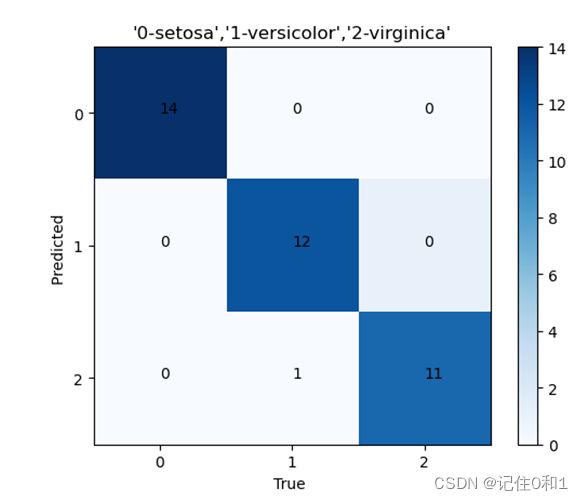
混淆矩阵是评判分类结果的好坏，通过下图可以看出0类和2类分类全部正确，1类有其中一个样本被误判为2类导使的分类错数；整个模型经过调参后效果达到预期目标。

决策树的可视化，选用Gini系数作为树分割的依据，通过可视化的结果也能看出深度为3时，分类结果最好。

import pandas as pd
from sklearn.preprocessing import LabelEncoder, StandardScaler
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.metrics import accuracy_score,confusion_matrix
from sklearn.tree import DecisionTreeClassifier
import graphviz
import matplotlib.pyplot as plt
import keyboard
from pandasgui import show
data = pd.read_csv('iris.csv')
show(data) #通过pandasgui封装好的API来分析数据
print(data.head(15))#查看数据前15行

#单独拿出种类这一列进行类别编码
features = ["Species"]
for feature in features:#遍历整个类别
    data[feature] = LabelEncoder().fit_transform(data[feature])
print(data['Species'])#打印查看编码结果

#分割数据 还分为训练集个验证集
X = data.iloc[:,1:5]
y = data.iloc[:,5:]
X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.25,random_state=40)

#对数据进行标准化 让数据呈正太分布 也有利于减少计算
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
scaler.fit(X_valid)
X_valid = scaler.transform(X_valid)
print('X_train.shape: ', X_train.shape)

#通过键盘交互式开始训练和测试
if input(keyboard.wait('T')):
    depth = list(range(1,20))
    param_grid = dict(max_depth=depth)
    tree = GridSearchCV(DecisionTreeClassifier(),param_grid,cv=10,refit=True)#对深度进行调参
    tree.fit(X_train,y_train)
    means = tree.cv_results_['mean_test_score']
    params = tree.cv_results_['params']
    for mean,param in zip(means,params):
        for depth in param:
            mean_param = list([mean,param[depth]])
            plt.plot(mean_param[1],mean_param[0],'b*')
            plt.title('max_depth')
    plt.show()


    depth = list(range(2,30))
    param_split = dict(min_samples_split=depth)#分割内部节点所需要最小样本数
    tree = GridSearchCV(DecisionTreeClassifier(max_depth=3),param_split,cv=5,refit=True)
    tree.fit(X_train,y_train)
    means = tree.cv_results_['mean_test_score']
    params = tree.cv_results_['params']
    for mean,param in zip(means,params):
        for depth in param:
            mean_param = list([mean,param[depth]])
            plt.plot(mean_param[1],mean_param[0],'ko')
            plt.title('min_samples_split')
        # print('最终交叉验证完后：',tree.score(X_valid,y_valid))
        # print("每个超参数每次交叉验证得结果：",tree.cv_results_)
    plt.show()
    print("Best parameter:",tree.best_params_,
          "\nBest Score:",tree.best_score_)

    samples_split = list(range(1,30))
    param_leaf = dict(min_samples_leaf=samples_split)#叶子节点上最小样本数
    tree = GridSearchCV(DecisionTreeClassifier(max_depth=3,min_samples_split=2),param_leaf,cv=5,refit=True)
    tree.fit(X_train,y_train)
    means = tree.cv_results_['mean_test_score']
    params = tree.cv_results_['params']
    for mean,param in zip(means,params):
        for depth in param:
            mean_param = list([mean,param[depth]])
            plt.plot(mean_param[1],mean_param[0],'rd')
            plt.title('min_samples_leaf')
    plt.show()




    dt_model = DecisionTreeClassifier(max_depth=3,min_samples_split=2,min_samples_leaf=1)
    dt_model.fit(X_train,y_train)
    pred_train_results = dt_model.predict(X_train)
    predict_results = dt_model.predict(X_valid)
    from sklearn import tree
    #print('训练',accuracy_score(pred_train_results,y_train))
    print ('测试',accuracy_score(predict_results, y_valid))

    dot_data = tree.export_graphviz(dt_model,out_file=None)
    graph = graphviz.Source(dot_data)
    graph.render("tree")

    # 混淆矩阵
    confusion = confusion_matrix(y_valid,predict_results)
    plt.imshow(confusion,cmap=plt.cm.Blues)
    indices = range(len(confusion))
    plt.xticks(indices,['0','1','2'])
    plt.yticks(indices,['0','1','2'])
    plt.colorbar()
    plt.xlabel("True ")
    plt.ylabel("Predicted ")
    plt.title("'0-setosa','1-versicolor','2-virginica'")
    for first_index in range(len(confusion)):
        for second_index in range(len(confusion)):
            plt.text(first_index,second_index,confusion[first_index][second_index])
    plt.show()