矩池云 | 搭建浅层神经网络"Hello world"
作为图像识别与机器视觉界的 “hello world!” ,
MNIST (“Modified National Institute of Standards and Technology”)
数据集有着举足轻重的地位。基本上每本人工智能、机器学习相关的书上都以它作为开始。
下面我们会用 TensorFlow 搭建一个浅层的神经网络来运行 “hello world!” 模型。 以下内容和模块的运算,均在矩池云平台进行。
本次教程分五步:
第一步:数据预处理,包括提取数据标签、查看图片数据、数据可视化、查看数据是否平衡等
第二步:数据加载,打乱数据集
第三步:构建模型,简单介绍网络卷积模型和激活函数,定义训练函数和学习率
第四步:模型训练,查看训练过程和结果,使用图表查看模型精确度和学习率变化
第五步:尝试提升精准度,不断探索和优化
在搭建开始前,我们需要加载以下对应的模块:
第一步:数据预处理
1.1查看数据标签
在任何模型建立之前,应当优先查看数据的情况。例如数据集的大小、训练集和测试集的数据数量、标签的数据数量分布等。
下方为训练集和测试集的数据查看代码:
train = pd.read_csv('mnist/mnist_train.csv') # read train
test = pd.read_csv('mnist/mnist_test.csv') # read train
下方为训练集和测试集的数量结果:
train.shape (6000,785)
test.shape (10000,785)
我们可以看到 train 训练集里面有6000条数据,test 测试集里面有10000条数据,两个测试集每行都有785个数据。
接下来,我们来看下数据集的预览:其中第一列是标签列,剩余784列则为像素点数据,由该784列数据组成一张28*28的像素图片。
1.2 提取数据标签
接下来,我们进行数据标签的提取和处理。先来看下标签数据的提取代码:
train_labels = np.array(train.pop('label'))
test_labels = np.array(test.pop('label'))
查看标签种类,我们可以看出标签表示了从0~9的数字,没有其他的错误数据。
由于运算需要,我们需要将一维的图片数据转换成二维图片数据。将图片数据转换成长28,宽28,通道为1的格式,方便卷积计算。
第二步:数据可视化
2.1 随机生成数据匹配
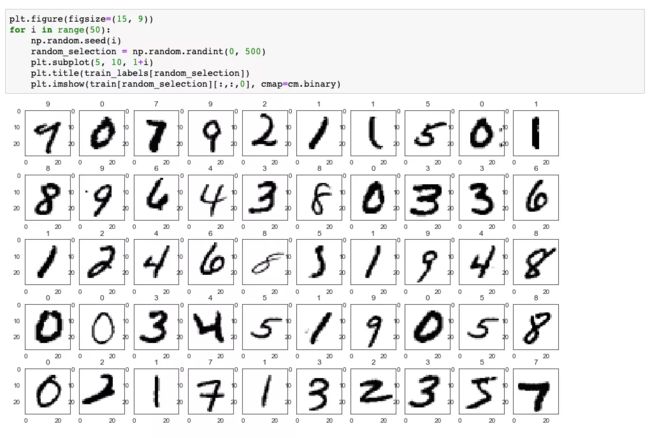
现在随机选取一些我们已经转换好的图片数据,用 matplot 来查看下标签和图片是否能够对上。
方框内是随机生成的一些非规则写法,图片上方正中间则为对应的数字。
2.2 查看数据是否平衡
分类器的设计都是基于类分布大致平衡这一假设,通常假定用于训练的数据是平衡的,即各类所含样本数大致相当。
下面我们来看下标签的分布情况,查看每个标签种类的数据量是否分布均匀。
在 MINST 数据集中,我们的数据是处于一个均匀分布的状态。
sns.distplot(train_labels, kde=False, bins=10)
2.3 数据加载
在建立模型之前,我们需要先定义一些常量:
# 图像宽度
width = 28
# 图像高度
height = 28
# batch size
batch_size = 100
# 训练图片数量
train_images_num = train.shape[0]
下一步,我们为模型建立数据集。TensorFlow 提供了 Dataset 类可以方便加载训练的数据,使用方式为 tf.data.Dataset。
其中,训练集的数据,我们进行了随机打乱。
train = tf.cast(train, tf.float32)
test = tf.cast(test, tf.float32)
train_ds = tf.data.Dataset.from_tensor_slices((train, train_labels)).shuffle(train_images_num).batch(batch_size)
test_ds = tf.data.Dataset.from_tensor_slices((test, test_labels)).batch(batch_size)
第三步:模型构建
3.1 构建模型的网络层次结构
数字识别作为入门工程,我们的模型也会相对的简单。当前构建模型,采用了以下几层网络层次结构:
- 第一层二维卷积层
- Flatten 层:这层的作用是将第一层的卷积曾平坦压缩成一维,常用在从卷积层到全连接曾的过度,当然 Flatten 不影响 batch 的大小
- Dense 层:全连接神经网络层
- Dense 层:全连接神经网络层
每一层对应的激活函数如下:
- 第一层使用 ReLU 函数
- Flatten 层( 无 )
- Dense 层 ReLU 函数
- Dense 层使用 softmax 损失函数进行输出
3.2 关于激活函数的解释说明
ReLU函数
ReLU 函数全名为线性整流函数(Rectified Linear Unit, ReLU),又称修正线性单元,是一种人工神经网络中常用的激活函数(activation function),通常指代以斜坡函数及其变种为代表的非线性函数。
ReLU的函数表达式为:
![]()
用向量形式表达为:
![]()
函数曲线形态为:
从函数的表达可以看出,函数抑制了比 0 小的输入,这个激活函数有以下特点:
- 收敛快
- 在[ 0, x ]区间内不会饱和,即它可以对抗梯度消失问题
- 求导简单,也就是它的计算效率很高
softmax 函数
softmax 用于多分类过程中,它将多个神经元的输出映射到(0,1)区间内,可以看成概率来理解,从而来进行多分类。
我们来看下它的数学表达式,假设我们有一个数组,V,Vi 表示 V 中的第 i 个元素,那么这个元素的 softmax 值就是:
在我们的数字识别的模型中,我们将最后的输出成一个10个元素的数组,数组从0下标开始到9,分别表示对应的标签。
然后对这个输出进行 softmax 计算,取出 softmax 值最大的那个元素对应的标签作为我们的分类结果。
class MNIST(Model):
def __init__(self):
super(MNIST, self).__init__()
self.conv1 = Conv2D(width, 3, activation='relu')
self.flatten = Flatten()
self.d1 = Dense(128, activation='relu')
self.d2 = Dense(10, activation='softmax')
def call(self, x):
x = self.conv1(x)
x = self.flatten(x)
x = self.d1(x)
return self.d2(x)
model = MNIST()
model.build(input_shape=train.shape
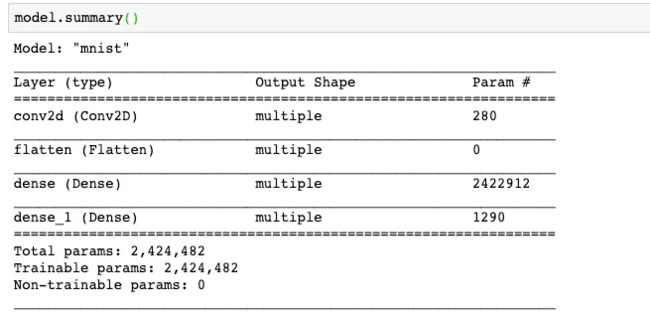
3.3 查看模型的构建情况
本文利用 summary 接口来查看模型的情况,可以看到我们的每层网络的类型、输出、参数的个数,最下面还是统计了可训练参数,全部参数的情况。
我们选用交叉熵函数作为我们的损失函数,基本公式如下:
batch 公式:
用随机梯度下降算法作为我们的优化器:
loss_object = tf.keras.losses.SparseCategoricalCrossentropy()
optimizer = tf.keras.optimizers.SGD()
train_loss = tf.keras.metrics.Mean(name='train_loss')
train_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='train_accuracy')
test_loss = tf.keras.metrics.Mean(name='test_loss')
test_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='test_accuracy')
定义 train_step 函数:
@tf.function
def train_step(images, labels):
with tf.GradientTape() as tape:
predictions = model(images)
loss = loss_object(labels, predictions)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
train_loss(loss)
train_accuracy(labels, predictions)
定义 test_step 函数:
@tf.function
def test_step(images, labels):
predictions = model(images)
t_loss = loss_object(labels, predictions)
test_loss(t_loss)
test_accuracy(labels, predictions)
一般情况下,学习率 ( learning rate ) 不适合设置为常数。在训练不断迭代的情况下,常量的学习率会导致模型收敛性变差。
在不断的迭代过程中,损失函数 ( loss ) 越来越小,因此我们希望学习率也越来越小,从而能够让模型收敛到一个更好的局部最优点。
这里我们简单的让学习率在每 epoch 中都以一定大小递减。
def lr_fn(epoch, lr):
if epoch == 0:
return 0.001
return lr * 0.9
设定一个较大的 epoch,我们在模型训练的时候做了 early stop 策略。当训练精度小于上一次 epoch 的精度,我们认为模型进入了过拟合了。
我们会停止训练这个也是一种防止过拟合的策略。
第四步:模型训练
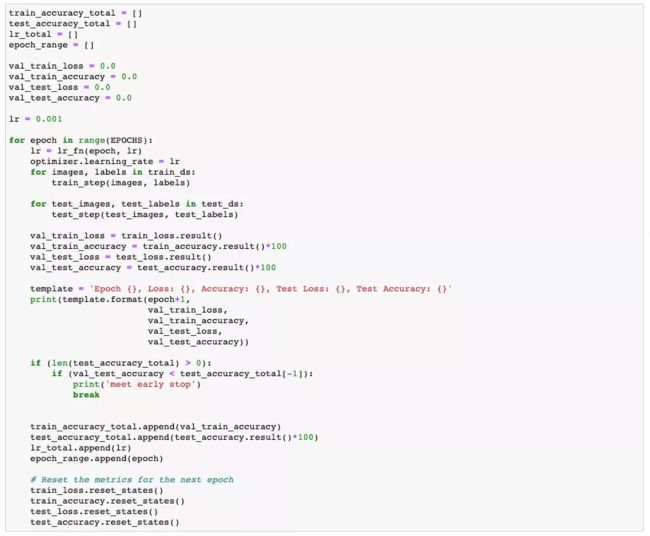
我们在训练中记录下了每一次 epoch 的训练集和测试集精度的统计以及学习率,为了训练完成后查看训练过程的效果。
我们可以看到的训练结果:
然后我们把训练中的记录下来的训练集和测试集的精确度结果放到图表中,用以查看我们的训练情况:绿色为测试集曲线,蓝色为训练集曲线。
plt.plot(epoch_range, train_accuracy_total, '-b', label= "training")
plt.plot(epoch_range, test_accuracy_total, '-g', label= "test")
plt.legend()
plt.xlabel('epoch')
plt.ylabel('accuracy')
从图表中可以看出,在经过不断的 epoch 迭代以后,模型的精度在开始的几个 epoch 后迅速提升(这表示收敛速度很快)。后面的几个 epoch 模型的精度曲线趋向于平稳,收敛速度放缓。
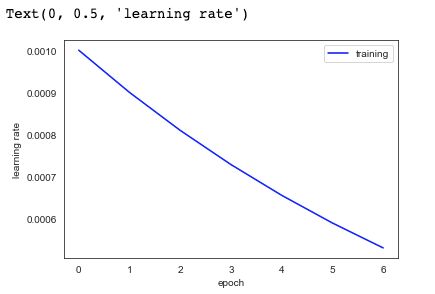
查看学习率的递减情况:
plt.plot(epoch_range, lr_total, '-b', label= "training")
plt.legend()
plt.xlabel('epoch')
plt.ylabel('learning rate')
第五步:探索和优化
后续读者可以从以下这几个方面来进行尝试,尝试提高模型的准确率。
- 更深的网络层次,可以更换模型,比如使用 VGG16,ResNet 等更深的网络,或者在现有的网络中添加更多的卷积层进行尝试
- 更多的训练数据,数据量的增长能极大的提高模型的精度跟泛化能力
- 使用别的优化器,比如:adam
- 调整学习率
矩池云现在已经全线上架 “机器图像识别” 镜像;
选择 “ 图像识别demo ” 镜像,机器启动后,在 JupyterLab 目录中选择
digit-recognizer 文件夹,矩池云已经将数据集和脚本都集成在其中,执行其中的 ipynb 文件,即可运行上述识别脚本。