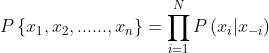【Learning PGM in R】第一章 概率推理

目录

1.1机器学习

1.1.1监督学习

1.1.2无监督学习和强化学习

1.2概率表示

1.2.1概率计算和随机变量

1.2.2条件概率、联合概率分布和边缘分布

1.3贝叶斯规则

1.4概率图模型基础

1.4.1概率图模型基础理论

1.4.2概率图的表示

1.4.3推断

1.4.4学习

参考文献

---

PGM（ stands for Probabilistic Graphical Models）, 是概率图模型的简称。概率图模型，隶属于机器学习。所以文章的第一小节首先介绍了什么是机器学习（Machine Learning ）。

机器学习的产生源于我们正处于数据大爆炸的时代中。数据的泛滥（deluge）使人们产生了数据分析的自动化（automated methods）的需求，并希望通过数据分析预测未来，获取知识或者进行决策。而这就是现在的机器学习。同时，数据本身的特征不同，再加上人们对数据处理的需求不同，从而创造出了各式各样丰富的机器学习模型和算法。

1.1机器学习

机器学习研究的问题大体上分为三个：监督学习，无监督学习和强化学习。

1.1.1监督学习

监督学习（predictive or supervised）的目的在于寻找输入x与输出y之间的关系（或是映射mapping，或是模式pattern），此时数据包括输入与输出，训练集，N是训练集数据对的数量，X可称作特征（ features）、属性(attributions)、协变量(covariates)、解释变量等;Y称作被解释变量（response variables）。而根据Y的不同，监督学习又可以分为：当Y是分类变量（categorical or nominal，如是否下雨问题上，用y=0表示不下雨，用y=1表示下雨）,研究的问题就被称作 分类（classification）和模式识别（pattern recognition）；当y表示真实的数值（身高，体重等），该类问题称作回归（regression）。而当Y本身具有一定的顺序性（如成绩A-F），该类问题成为有序回归（ordinal regression）。监督学习也是目前机器学习领域最常用，最泛化的部分。

1.1.2无监督学习和强化学习

而无监督学习（descriptive or unsupervised）与监督学习最大的区别子在于，这类问题没有Y，也就是说我们不知道我们要找的映射或者模式是怎样的，同时也没有已知的Y供我们测度（metric）模式的准确性。这类问题我们一般称为知识挖掘（knowledge discovery）。

第三类问题是强化学习（reinforcement learning），在处理该问题时，我们会设置偶然激励（occasional reward）和惩罚信号（punishment signals）来引导模型学习什么是正确的行为。

1.2概率表示

在解决机器学习问题上，不确定性（uncertianty）是一直伴随的。事件发生的结果是不确定的，我们预测的准确性也是不准确的，概率（probability）相关的理论就可以应用到机器学习的问题上，用于表达不确定性以及不确定性的程度。

1.2.1概率计算和随机变量

在进行实验时，我们对实验的结果有一定的预期，这个由实验所有可能输出组成的集合叫做样本空间，记作（donated by）。每一种输出都被记作一个事件，记作。而我们在计算机中储存实验结果时，往往会使用实数代替，也就是样本空间到实数的函数映射，被称为随机变量（random variable）。

---

如下雨，实验结果可能为Ω={下雨，不下雨}两种，我们将其记作y，y = 1的时候下雨，y = 0的时候不下雨。这时y就是随机变量。

---

而对于每一个随机变量y，都有唯一确定的概率密度函数（probabilistic density function, pdf for short）与之对应，记作p(y)。一般地，概率分布包括离散型（discreted）分布和连续型（continuous）分布，如是否下雨符合0-1离散分布，人的身高服从（falls into）高斯分布（Gaussian distribution）。

1.2.2条件概率、联合概率分布和边缘分布

而在进行概率计算时，我们往往不只单看一个变量。如在考虑下雨问题时，我们会考虑下雨（x）和堵车（y）之间的关系，这种考虑两个或多个事件同时发生的概率，称作联合概率分布，记作。如我们会考虑如果昨天下雨了，那么今天会下雨吗？这时，我们设置了一个条件：昨天下雨了。这种在已知其他事件D发生的条件下当前事件x发生的概率叫做条件概率，公式如下：

如果我一直增加实验和变量，我们可以写出很长很复杂的条件概率分布和联合概率分布。有没有什么方法可以简化呢？条件独立的概念就被引入进来了。当观测变量x与y之间是独立的时候，联合概率为。条件概率为，这将大大简化运算的复杂程度。

此外还有个重要的边缘化概念，即当X,Y不是独立的时候，当我们已知X,Y的联合概率分布，为了得到x的分布，我们会将Y通过加和或积分的方式积分掉，从而获得X的边缘分布。公式如下，当Y是离散型随机变量时，联合分布的边缘分布为：

如果Y是连续值，边缘化就写作积分的形式：

1.3贝叶斯规则

贝叶斯公式的基本形式就是由条件概率和边缘分布演化来的。我们都知道条件概率为或是，简单变换后，我们可以得到。此外，根据边缘化理论，，所以，最终贝叶斯公式为：

为什么要用这样的形式呢？联系一下我们实际的任务，并且转换一下公式的符号。假设我们在求解掷硬币正面反面的概率，用表示掷硬币的结果，0代表反面，1代表正面,表示掷硬币为正面的概率。假设我们已经进行了n次实验，实验数据集记为，.此时，我们先假定一个，假设为0.5，在已知数据集（即进行了n次实验）的情况下，更改为（这里我复杂了式子的表达，以便大家理解贝叶斯公式）：

 首先我们可以看到，分子上面的是提前假定的，这叫做先验分布（prior distribution），给定了这样的先验分布后，数据集发生的概率为，记作似然率（likelihood）。观察到了这样的,的分布会发生变化，新的（其实是）就可以计算出来了，被称为后验分布（posterior distribution）。

1.4概率图模型基础

我们已经知道，将概率的理论应用到机器学习问题中表示不确定性是自然而然的事情。而用图表示概率模型，可以更好的表达现实问题。由于现实世界的复杂度，我们观测的变量往往是高维多元的，随着研究问题中的变量的不断增加，记录每一种结果需要的值正在以指数级的速度增长。

---

如，假设我们有10个二元变量，储存可能出现的结果需要2^10= 1024个值，如果有20个变量，那么就需要2^20 = 1048576个值。假设变量本身是连续性分布，假设变量数量继续增加......

---

此外，变量间的关系变得逐渐复杂，变量间的依赖关系也造成了建模的困难。因此，机器学习引入了图论的相关知识，通过图来描述研究问题，可以迅速理清变量间的依赖关系，并根据条件独立的性质使得表达式最简化。

1.4.1概率图模型基础理论

回顾贝叶斯规则部分，通过简单变换，我们得到联合概率分布，这里变量只有X，Y。我们假设变量集，此时有

其中，。这就是著名的链式法则（Product Rule or Chain Rule）。

假设有数据集，其中，通过将联合概率分布积分获得的边缘分布

 这就是和法则（Sum Rule）。通过两种法则获得的贝叶斯法则（Bayesian Rule）,被称为和积变换：

为了简化模型，概率图模型具有以下假设

假设1.变量之间相互独立。因此。（朴素贝叶斯的重要假设）。但是这样的假设太强了，很多现实情况并不符合，可用性不强。因此我们对条件进行了放松：

假设2.马尔可夫性（Markov Property）：给定当前时刻的情况下，将来与过去无关。（马尔科夫链的重要假设）即。但其实这个假设依旧太单调了。因此我们开始再次放宽假设。

假设3.条件独立性假设，记作，意思是在给定的情况下，与互相独立。其中，，，都是变量集合且互不相交。

假设3这是概率图模型的重要假设，借助概率图模型，我们可以直观地看出变量间的条件独立性。

 概率图模型的内容主要包括表示（representation），推断（inference）和学习（learning）。

1.4.2概率图的表示

概率图使用节点（node）来表示变量。节点与节点之间的边（edge）代表随机变量间的关系。

当这个边有箭头时，箭头起点的节点为父节点，箭头指向的节点为子节点，边就表示条件概率，由有向边和节点组成的图称为有向图（Directed Graph）也称为贝叶斯网络（Bayesian Network），常用于变量间的因果分析。而当这个边的没有箭头时，就是无向图（Undirected Graph），也称为马尔可夫网络（Markov Network）。

1.4.3推断

推断，即给定已知数据的情况下，求变量的概率分布。根据方法最终得到的分布是否精确又分为精确推断和不确定性推断。近似推断中又包括确定性近似（如变分推断）和随机近似（如MCMC）。

1.4.4学习

学习，概率图中分为结构学习（structure learning）和参数学习（parameter learning）。结构学习，给定的数据可以学习哪种图结构更符合数据集。参数学习是在概率分布的模型已经假定好的情况下，估计出模型中参数的值。而在参数学习中，当数据不是完备的(complete data)，我们需要引入EM算法进行参数估计。

参考文献

[1]David Bellot. Learning Probabilistic Graphical Models in R. Packt Publishing, 2016

[2]Murphy, K.P.. Machine Learning A Probailistic Perspective. The MIT Press, 2012

参考视频：

【机器学习】【白板推导系列】【合集 1～23】_哔哩哔哩_bilibili