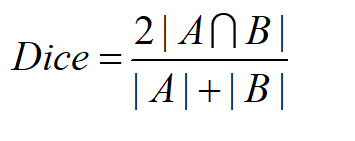图像分割之Unet原理简介与代码简析
Unet论文地址:
A Nested U-Net Architecture for Medical Image Segmentation
Unet是比较早的基于深度学习的分割算法了,优点是速度真的快(P100上基于VGG的backbone能跑到50帧),同时不是太开放的场景下可以做到令人满意的分割效果,在对实时性要求较高的场合下是比较适用的(不是所有的场合都能上MaskRCNN的,Backbone大一点,如果显卡差点就容易爆显存了。。),同时相比大分割网络的模型动辄几百Mb,Unet用小backbone模型就可以做到10Mb内,Conv层通道减少一点再把网络模型参数分开,模型大小可以做到很小,用CPU跑速度都挺快的,关键是分割精度在较为简单场景下还可以,load速度快太多了,简单,效果好,速度快,这也就是Unet为什么这么受欢迎的原因,下面是Unet原理介绍:
Unet结构可以说是相对比较简单的图像分割算法了,通过四个下采样提取目标特征,再通过四个上采样,最后逐个对其像素点进行分类,那么这实际上是一个基于编码器(encode)-解码器(decode)思想,选用四个block做下采样的原因论文作者好像并没有说明,个人理解是因为是更适合测试数据集?
既然说到编码器-解码器,我的个人理解是编码器实际上相当于backbone对输入图片进行特征提取,提取出合适的feature-map,再通过解码器恢复至原尺寸,进行逐个像素点分类。
例如输入1281283的图片,输入网络后的输出为1281281的mask,
以下是一个最简单的下采样block:
x = Conv2D(64, (3, 3), padding='same', name='block1_conv1')(input)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(64, (3, 3), padding='same', name='block1_conv2')(x)
x = BatchNormalization()(x)
b1 = Activation('relu')(x)
x = MaxPooling2D()(b1)
下采样过程其实没有什么特别值得说明的,就是简单的卷积层特征提取。
上采样:
输入图像经过前面下采样进行特征提取之后,需要把图像恢复至原来的尺寸以便进一步对像素进行分类(所谓的语义分割),那么这个过程也就是上采样。
一般来说上采样方法常见的有:双线性差值(bilinear),反卷积(Transposed Convolution),还有就是反池化(Unpooling),Unet的上采样就是通过反卷积实现的。
反卷积实质上来说是转置卷积,早在2011年被Zeiler提出,这里简单介绍一下反卷积,详细介绍请看这里
卷积的前向计算可以看做是参数矩阵和输入矩阵相乘,Y是输出,C是参数矩阵,X是输入矩阵
这里注意的是,反卷积只是为了恢复图像shape,而不是为了恢复图像像素,所以并不是完全的逆运算,反卷积实质还是一种卷积。
Unet中一个标准的上采样block,注意这里运用了一个跳连接把前面的特征图和上采样后的特征图concat到一起(类似resnet的思想),目的是使得上采样后的特征图具有更多的浅层语义信息,增强分割精度,这里注意,最后一层直接一个sigmoid二分类把mask分为前景和背景。
x = Conv2DTranspose(256, (2, 2), strides=(2, 2), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = concatenate([x, b3])
x = Conv2D(256, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
x = Conv2D(256, (3, 3), padding='same')(x)
x = BatchNormalization()(x)
x = Activation('relu')(x)
分类:
最后一层,通过sigmoid完成前景和背景分类
x = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
损失函数:
简单说明一下图像分割中的损失函数:
Unet的损失函数其实就是一般的图像分割损失函数
常见的图像分割损失函数有,Binary crossentropy,dice coefficient,focal loss(解决类别不平衡),这里以dice_loss举例
一般为:
具体代码实现:
from keras import backend as K
smooth = 1.
def dice_coef(y_true, y_pred):
y_true_f = K.flatten(y_true)
y_pred_f = K.flatten(y_pred)
intersection = K.sum(y_true_f * y_pred_f)
return (2. * intersection + smooth) / (K.sum(y_true_f * y_true_f) + K.sum(y_pred_f * y_pred_f) + smooth)
def dice_coef_loss(y_true, y_pred):
return 1. - dice_coef(y_true, y_pred)