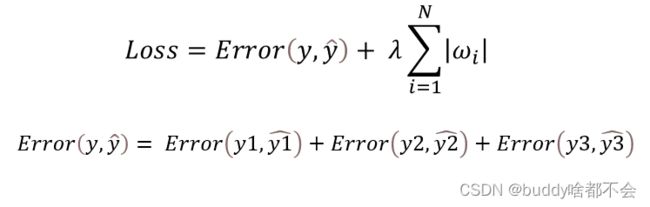深度神经网络——LSTM作曲机的实现

       随着人工智能技术的不断发展，人工智能作曲已经成为可能。现有的神经网络作曲方法，主要是基于循环神经网络，变分自动编码器或生成对抗网络实现的。其中，RNN是专门处理序列数据的网络，但是标准RNN无法解决长期依赖问题。Hochreiter和Schmidhuber在标准RNN的基础上进行了改进，提出了长短时记忆网络（LSTM），很好地解决了长期依赖问题。

       本次实验通过LSTM实现了一个能自动生成音乐的作曲机，以一首莫扎特的Krebs乐曲为训练数据，生成了数曲风格类似，还算动听的音乐。实验主要分为五大步骤，分别为MIDI音乐文件的解析，数据集的准备，神经网络的建立，训练网络以及音乐的生成。本实验采用三通道拼接+拆分的网络结构，还通过改进的损失函数缓解了模型的过拟合问题。

实验环境：Python3.8，torch 1.11.0+cu113，mido1.2.10，代码在Google colab上运行。

一、网络简介

1、整体架构

网络的输入由音符、速度、时间三个编码后的向量拼接而成，经过一层LSTM和一层全连接层，三个分量被重新切分开，分别进行LogSoftmax并计算损失，这种三通道拼接+拆分的方法有利于模型捕获不同序列之间的关系。

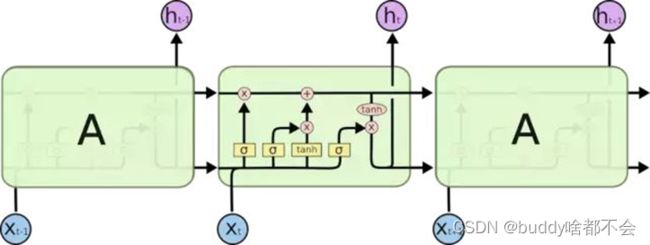
2、LSTM结构

LSTM的关键是细胞状态Ct，也就是图中顶端水平线上传送的向量。LSTM可以通过“门”结构对细胞单元中的信息进行删除或添加，门是一个可以让信息选择性通过的结构，通常由一个sigmoid函数和一个按位乘运算组成，sigmoid函数可以理解成门开的大小，决定了信息通过量。

用LSTM自动作曲具有以下优点：1.不需要提前计算时间序列的参数；2.对时间序列数据的性质没有过多要求，适用范围较广；3.可以学习到时间序列内部复杂的规律，而不只是机械的针对某些固定因素；4.可以捕捉时间序列的长期依赖关系。

3、损失函数

实验中定义的损失函数如下，包括三个分量的损失之和，还添加了L1正则项，防止模型的过拟合。

其中，1，2，3为的三个分量，分别对应note，velocity和time。

由于网络最后一层定义的是LogSoftmax，即为Softmax取对数，这里计算预测损失为Negative Log-Likelihood Loss（NLLLoss），这种LogSoftmax + NLLLoss的效果等价于CrossEntropy Loss，但能解决函数上溢和下溢出的问题，加快运算速度，提高数据稳定性。

二、主要步骤

1、MIDI音乐文件的解析

MIDI格式文件主要存储了具体的音乐序列（音轨）及序列中每个时间点的音符信息，每个乐器部分又由按时间顺序排列的音符（包括和弦）序列组成，主要以数字和字母组合的音高符号来记录。

每个MIDI文件由多个音轨组成，每个音轨都可以独立代表一个乐器，每个音轨包含若干条消息，消息可解释为相应音符，一条消息可以记录为[type, note, velocity,time]的形式。

• type确定信号的类型，‘note_on’作为音符开始，‘note_off’作为音符终止；
• note确定音符的音高，取值范围为0~88，每增加12，音高升高一个八度；
• velocity确定音符的音量，取值范围为0~127；
• time表示距离上一个音符的时间长度，是一个连续取值的实数序列。

本实验基于‘krebs.mid’音乐文件，仅提取第一个音轨（钢琴音轨）的消息序列，由于我们只对消息序列中的音符信息感兴趣，我们将提取音符消息作为数据集，一条音符消息表示为[note, velocity, time]，存储于notes变量中。

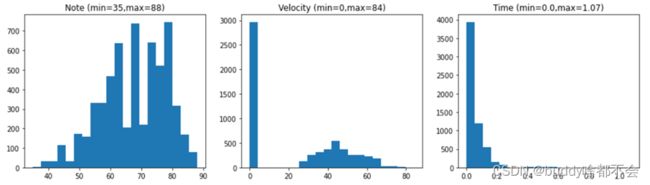
绘制音符消息中三个分量的直方图，容易看出各个分量取值的分布情况，求出最大值和最小值，根据各分量的取值情况进行下一步数据的处理。

 2、数据集的准备

在步骤1中，我们得到了很多条形式为[note, velocity, time]的数据，训练之前我们还需要对其进行编码处理。其中note和velocity都可以看作是类型变量，而连续的变量time首先需要转化为离散的。如下代码中对time进行划分成0~11区间，将原始的time=0单独分为一类。

for循环实现了对每一条消息的编码，这里的One-hot编码具体实现方式为，首先初始化一个长度为(89+128+12)的全0数组，然后将三个变量的值作为下标，赋予数组中的相应位置的值为1，得到了编码后的数据集dataset。

编码后的每一条消息都为一个长度为229的slot，dataset为所有消息的集合。

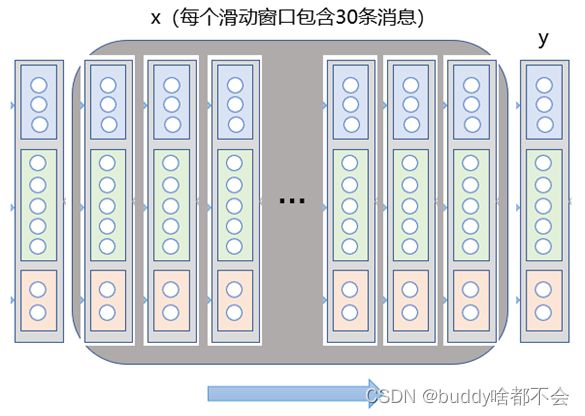
然后进行数据集的生成。以大小为30的滑动窗口在dataset中进行循环，每一组共30条消息作为LSTM的输入x，该组后一条消息作为目标输出y；所有的x与对应y的集合分别得到了数据集X和Y，将X和Y中元素打乱重排后，以9：1切分训练集和验证集。

PyTorch提供了TensorDataset和Dataloader用于转换和加载数据集的方法，该方法在预处理时会将数据集分为batch，调用一次Dataloader便能加载一个batch的数据。

3、神经网络的建立

（1）定义一个LSTMNetwork类，该类继承了神经网络模块nn.Module，其中实现了类的初始化、前向传播以及隐藏层的初始化。主要函数包括以下。

1）def __init__(self, input_size, hidden_size, out_size, n_layers=1)

定义了网络的基本参数，以及网络中各层的初始化，包括0.5的Dropout层；

2）def forward(self, input, hidden=None)  实现网络的前向传播；

3）def initHidden(self, batch_size)

（2）在本模型中自定义了一个损失函数如下，原损失函数由三部分组成，分别对应note, velocity, time的交叉熵，NLLLoss + LogSoftmax等价于CrossEntropyLoss。同时在原损失函数中还加入了L1正则项，防止模型的过拟合。

（3）自定义准确率函数如下，对于每个样本的输出值的第一个维度求最大，其下标作为预测的类别，与labels中包含的类别进行比较，返回预测正确的数量与标签的总个数，用于之后计算准确率。

 4、训练网络

定义一个LSTM，输入参数分别为input_size, hidden_size, out_size，另外num_layer默认为1。

定义一个Adam优化器，学习率设置为0.001，权重衰减率为1e-5。

初始化loss和records列表为空。训练轮数设置为200轮。

开始训练，训练过程包括前向传播，反向传播和梯度的更新。

在每轮参数更新后在验证集上循环遍历一次，计算模型在验证集上的损失和准确率， dropout仅在训练阶段有效。

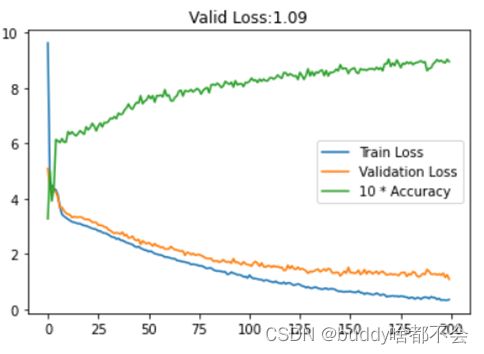
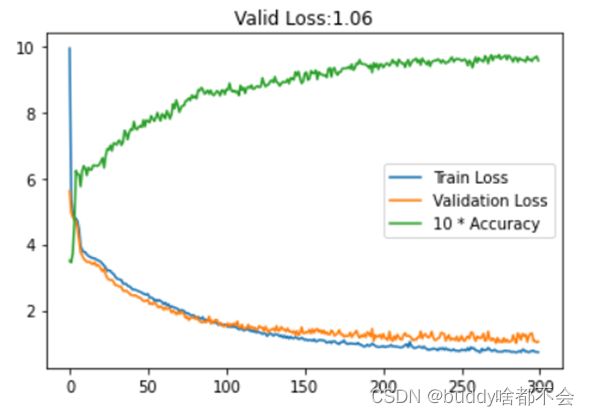
以下为损失值和准确率变化曲线，上图为未加正则项的原模型，下图为L1正则化后的模型。可以看到，L1正则化较好缓解了原模型的过拟合。

 训练200轮后，模型在验证集上达到0.97的准确度。

 5、音乐生成

进而，用训练好的LSTM模型来生成新的音乐。简单起见，这里直接用训练数据乐曲的前30个音符作为种子输入LSTM，然后将预测值加入到输入数据的最后面，删除第一个消息，再输入LSTM，如此循环往复得到音符序列的生成。

在生成阶段，是将输出层按照随机的方式来采样生成序列，而不是根据最大概率的方式，这样做的好处能够保持输出乐曲的多样性。

最后，将生成的序列转化为MIDI格式的消息，并保存MIDI音乐。

生成的MIDI文件用MidiSheetMusic-2.6.2打开，可以查看五线谱的格式，还可以在进行播放的过程中标记音符。以下为生成的部分音乐片段。

三、实验总结

       本次实验通过LSTM实现了一个能自动生成音乐的作曲机。网络总体架构采用三通道拼接+拆分的方式，有利于模型捕获音符、速度和时间三个序列之间的关系，而通过LSTM结构可以捕捉序列的长期依赖关系。

       本实验中一个很重要的问题就是避免过拟合，在实验中我也尝试过多种方法来缓解，比如减少隐藏层神经元的数量，使用更大的Dropout，L1、L2正则化等等，最后结果显示，在损失函数中加入L1正则化项是一种相对较好的办法，这种方法改进后的模型在验证集上达到了0.97的准确率，相比原模型有了较大的提升。

       随着人工智能技术的不断发展，其在各行各业的应用层出不穷，从早年的写诗、绘画、当主持人，到最近化身“音乐人”，以小冰为代表的人工智能正不断介入到文艺创作领域。看似LSTM能够“吟诗作曲“，好像是在创作，其实是一种模仿。只不过由于计算机计算能力的强大，这个模仿不容易被识破而已。