深度强化学习篇1：神经网络回归实例---复杂函数拟合

一、TensorFlow2

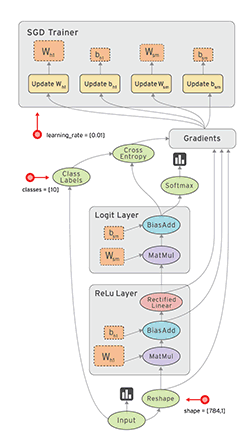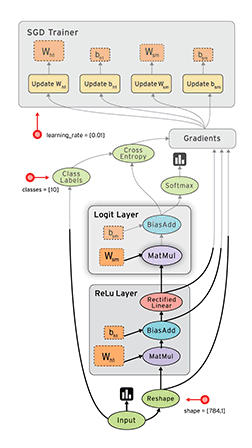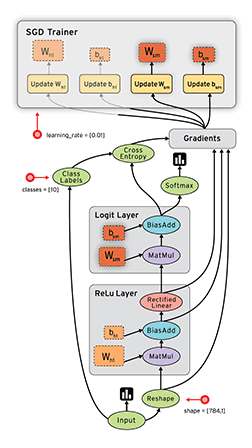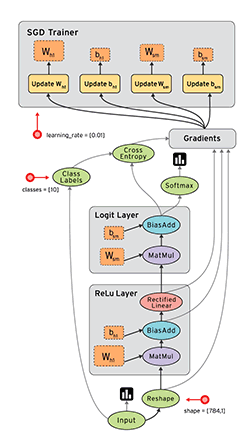
TensorFlow的张量与数据流图：一维张量如向量，二维张量如矩阵，以此类推。TensorFlow的数据流图如下。

                                                                  

二、神经网络基础编程实例

1、TensorFlow例程1——TensorFlow结构，优化器逼近函数参数

import tensorflow as tf
import numpy as np

# 数据
x_data = np.random.rand(100).astype(np.float32)
y_data = x_data*0.1 + 0.3
# 权重和偏置
Weights = tf.Variable(tf.random_uniform([1], -1.0, 1.0))
biases = tf.Variable(tf.zeros([1]))
# 估计y
y = Weights*x_data+biases
loss = tf.reduce_mean(tf.square(y-y_data))
# 设置优化器
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
# 初始化全部变量
init = tf.initialize_all_variables()
# 设置对话
sess = tf.Session()
sess.run(init)
for step in range(201):
    sess.run(train)
    if step % 20 == 0:
        print(step,sess.run(Weights),sess.run(biases))

2、TensorFlow例程2——构建三层神经网络预测函数输出(300一维数据输入，输出预测值，损失函数为误差平和方均值)

一维数据输入，全连接层10个神经元。

import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
import numpy as np
import matplotlib.pyplot as plt
plt.ion()
plt.show()

def add_layer(inputs, in_size, out_size, activation_function=None):
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    # 神经网络预测值
    Wx_plus_b = tf.matmul(inputs, Weights) + biases
    # 激励函数
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)
    return outputs

# 构建数据
x_data = np.linspace(-1,1,300, dtype=np.float32)[:, np.newaxis]
noise = np.random.normal(0, 0.05, x_data.shape).astype(np.float32)
y_data = np.square(x_data) - 0.5 + noise

# 定义输入
xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])

# 定义隐藏层
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)

# 定义输出层
prediction = add_layer(l1, 10, 1, activation_function=None)

# 损失函数：误差平方和求均值
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1]))

# 优化器最小化损失函数
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

# 初始化变量
init = tf.global_variables_initializer()

# 开启会话
sess = tf.Session()
sess.run(init)

# 显示图片框
fig = plt.figure()

# 连续画图ax,数据点
ax = fig.add_subplot(1,1,1)
ax.scatter(x_data, y_data)

# 训练
for i in range(5000):
    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
    if i % 50 == 0:
        # print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))
        # 除了第一次,抹除之前预测线
        try:
            ax.lines.remove(lines[0])
        except Exception:
            pass
        prediction_value = sess.run(prediction, feed_dict={xs: x_data})
        # 把预测用一条线表示
        lines = ax.plot(x_data, prediction_value, 'r-', lw=5)
        plt.pause(0.1)
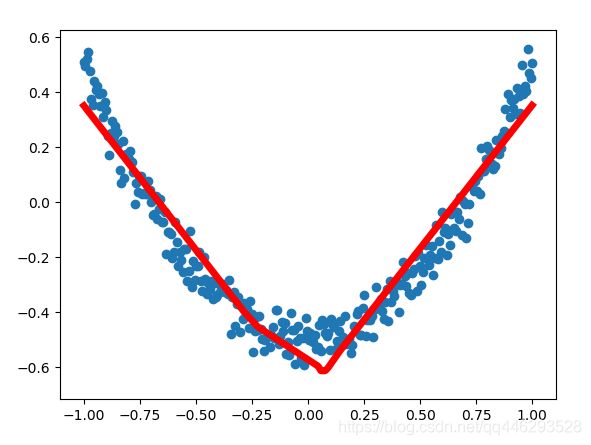
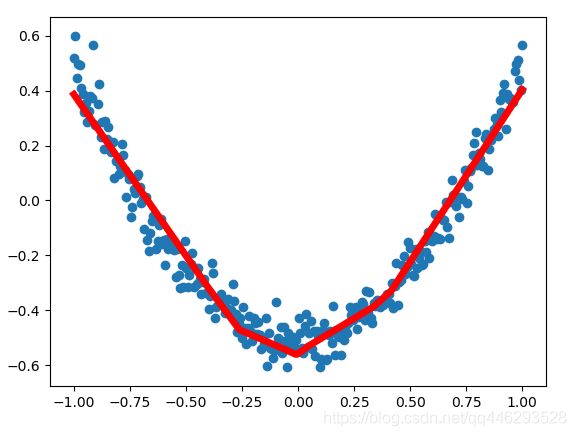
        print(sess.run(loss, feed_dict={xs: x_data, ys: y_data}))

 

训练500次，每50次可视化一次预测曲线。 

              

训练5000次，10个神经元，lost：0.00242。 训练5000次，30个神经元，lost：0.00262。神经元的增加并没有降低lost。

                                                     

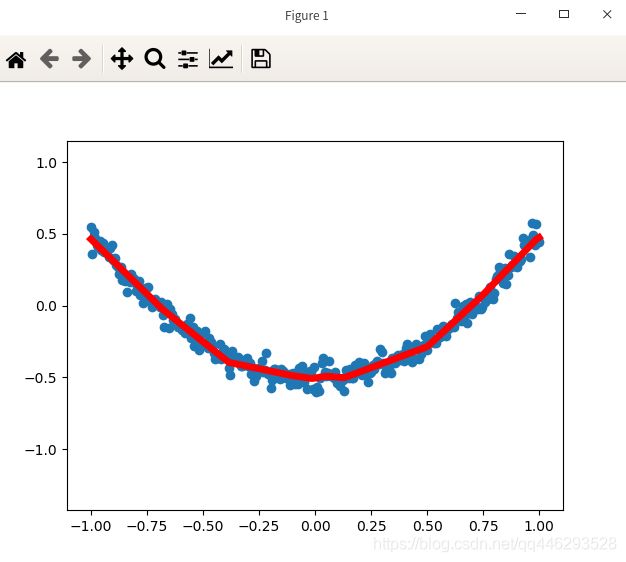
                                                                            300数据，训练5000次，10个神经元

                                                          

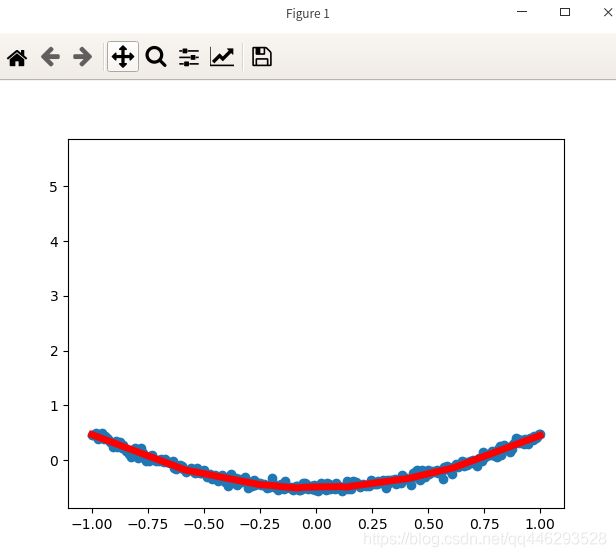
                                                                             100数据，训练5000次，10个神经元

注：tensorboard左侧的工具栏上的smoothing，表示在做图的时候对图像进行平滑处理，这样做是为了更好的展示参数的整体变化趋势。如果不平滑处理的话，有些曲线波动很大，难以看出趋势。0 就是不平滑处理，1 就是最平滑，默认是 0.6。

可视化进阶1：https://blog.csdn.net/wgj99991111/article/details/84294450  Tensorflow的可视化工具Tensorboard

可视化进阶2：https://blog.csdn.net/Charel_CHEN/article/details/80364841 tensorboard 平滑损失曲线代码

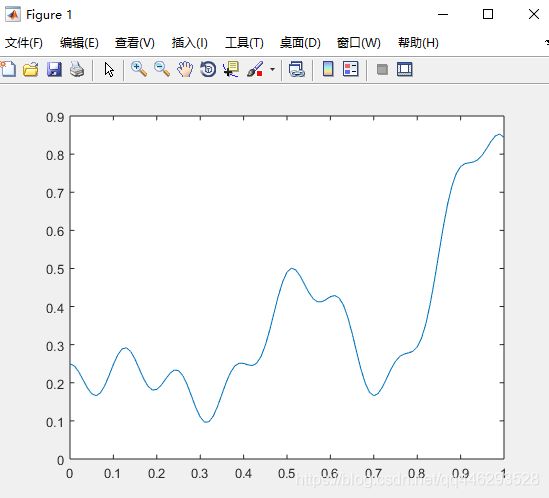
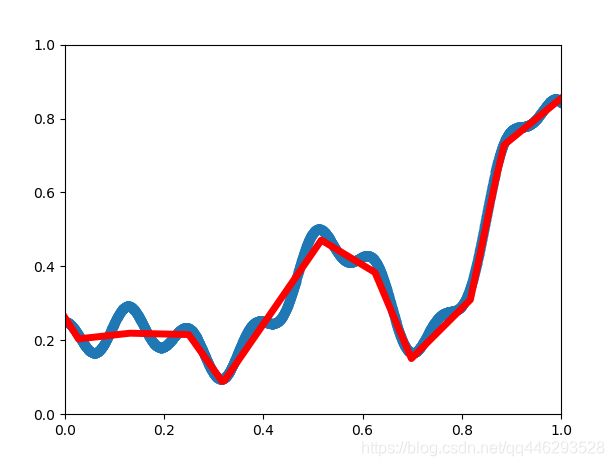
3、TensorFlow例程3——建立神经网络来拟合下图函数

    （目标函数f(x)=0.2+0.4x2+0.3sin(15x)+0.05cos(50x)f(x)=0.2+0.4x2+0.3sin(15x)+0.05cos(50x)）

                                                                

                                                              

两层隐含层构建神经网络拟合复杂函数曲线，lost收敛至0.000743。

三、全连接层总结

1、曲线拟合主要使用全连接层，理论上一层全连接层的神经网络就可以拟合所有连续函数。

2、全连接层的参数：

1. 全接解层的总层数（长度）
2. 单个全连接层的神经元数（宽度）
3. 激活函数

3、参数的影响：

如果全连接层宽度不变，增加长度。神经元个数增加，模型复杂度提升；全连接层数加深，模型非线性表达能力提高。理论上都可以提高模型的学习能力。

如果全连接层长度不变，增加宽度。神经元个数增加，模型复杂度提升。理论上可以提高模型的学习能力。

如果长度宽度都增加。学习能力太好容易造成过拟合。运算时间增加，效率变低。

参考链接：https://www.zhihu.com/question/41037974/answer/320267531  全连接层的作用是什么？

%一些记录

权重与偏置： 控制信号的重要性 ，权重越大，对应信号越重要。偏置是神经元被激活的容易程度，偏置越小越容易激活。

感知机的局限：只能用一条直线分割空间，无法实现异或。但是可以通过多层感知机实现异或。

计算机与感知机：与非门的组合再现计算机的处理，因此多层感知机也可以表示计算机处理。

神经网络与感知机：感知机使用阶跃函数做激励，人工调权重。神经网络使用平滑激励函数，从数据中学习权重参数。感知机中流动的是0,1二元信号。激励函数使神经网络实现平滑性，流动连续的实值信号。

激励函数的选择：激励函数如果使用线性函数，不管如何加深层数，总存在与之等效的无隐藏层神经网络，使加深网络失去意义。关于输出层的激活函数，回归问题用恒等函数，分类问题用softmax函数。

其它：层号从零开始，便于Python实现。输入到输出的（前向）运算。前向表示输入到输出的方向的传递处理。神经网络的推理处理也叫神经网络的前向传播。神经网络可以用在分类和回归问题上，根据需要改变输出层的激活函数。