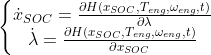基于极小值原理的功率分流式混合动力汽车能量管理策略研究

目录

0 引言

1 功率分流式混合动力汽车系统构型

1.1动力系统构型

1.2 发动机模型

1.3 电机模型

1.4 电池模型

1.5 整车动力学模型

2 基于极小值原理的能量优化策略

2.1 能量管理最优问题提出

2.2 基于Pontryagin极小值原理控制策略的构建

2.3 基于Pontryagin极小值原理控制策略求解

3 仿真实验及结果分析

4 结论

---

0 引言

       混合动力汽车由于其低油耗的特点而成为当今研究的热点，对于拥堵工况更能显示出其节能的优势。混联式混合动力汽车兼有串联式和并联式结构的优点，能够实现低速纯电动起步和大功率制动能量回收，避免了发动机在低速低负荷工况低效率运行和频繁制动的能量损失，因此更适于拥堵工况运行。由于混合动力系统存在多个动力源，即电池、内燃机和电动机等，能否均衡协调控制各动力部件间的功率分配成为其节油的关键，对混合动力汽车能量管理策略进行优化就显得特别重要。研究者们为获得混合动力系统能量管理的全局优化控制策略而引入了各种优化算法。本项目针对一款功率分流式混合动力汽车进行全局优化控制策略设计。

1 功率分流式混合动力汽车系统构型

1.1动力系统构型

        本项目的研究对象为功率分流式混合动力汽车，其系统结构形式如图1所示，该系统具有 3个动力源(发动机、电机MG1和电机MG2)和1个行星排。行星排为该系统的功率分流机构。发动机的输出轴连接着行星排的行星架，电机MG1的输出轴连接着行星排的太阳轮，电机MG2的输出轴连接着行星排的齿圈，并将整个系统的动力输出到主减速器。该构型可实现纯电动( EV)模式、混合动力 ( EVT) 模式和再生制动(RGB)模式等多种工作模式。

图1 功率分流式混合动力汽车结构示意图

1.2 发动机模型

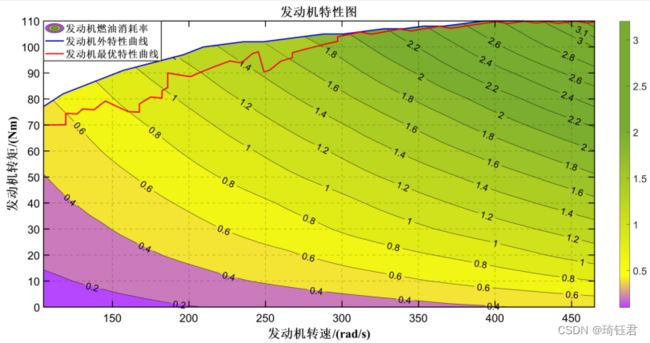
       本项目的系统构型可以实现发动机与车轮之间的双重解耦，因此发动机的工作点不会受到车速的影响，故可以通过自由调节发动机的工作点，使其工作在最佳的油耗区域，从而达到节能的目的。综合以上分析，可以结合发动机的万有特性图建立简化的发动机模型

(1)

式中， 为发动机输出扭矩； 为发动机转速；为单位时间内的燃油消耗量，可通过一定转速和转矩查找准静态发动机万有特性MAP图得到。

图2 发动机MAP图

1.3 电机模型

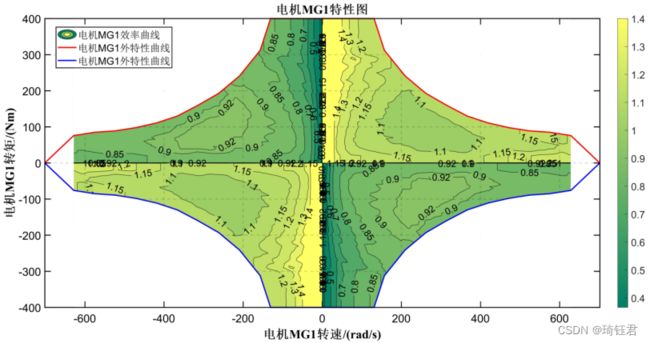
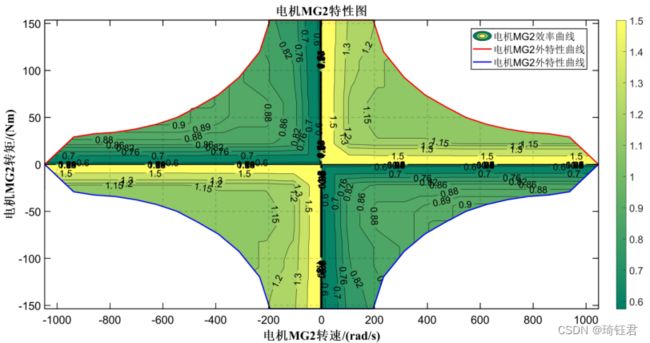
       车辆在运行过程中，电机既可作为电动机工作，也可作为发电机工作，所以电机的电功率计算模型可表示为

(2)

式中，为电机电功率；为电机输出扭矩；为电机角速度；为电机效率，可通过一定转速和转矩查找电机准静态效率MAP图得到。

图3 电机MG1MAP图

图4 电机MG2MAP图

1.4 电池模型

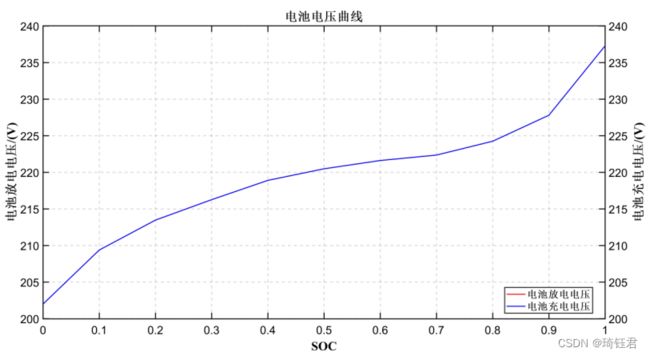
       混合动力汽车的动力电池组可以等效为一个由电压源和电池内阻串联组成的电路，所以电池电荷状态变化率可表示为

(3)

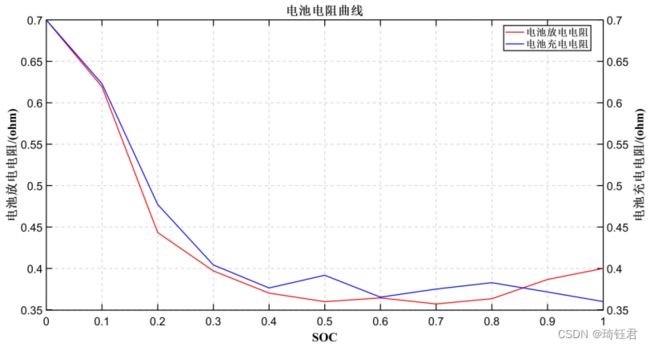
式中，为开路电压；为电池容量；为电池内阻；为电池功率。开路电压、电池内阻与电池SOC的关系如图5-7所示。

图5 电池开路电压与SOC的关系曲线

图6 电池内阻与SOC的关系曲线

图7 电池电流限值与SOC的关系曲线

1.5 整车动力学模型

       汽车行驶过程的纵向动力学平衡方程为

(4)

式中，为作用在车轮上的驱动力矩； 为作用在车轮上的制动力矩；为整车总质量；为滚动阻力系数；为车速；为空气阻力系数；为迎风面积；为道路坡道角；为旋转质量换算系数；为车轮半径。

2 基于极小值原理的能量优化策略

2.1 能量管理最优问题提出

       为了最大限度降低混合动力车辆的燃油消耗，能量管理控制问题可以转化为一个最优控制问题。其优化目标是使车辆从起始到终止时刻的燃油消耗最小。整个行驶过程中的燃油消耗表示为

(5)

式中，为可行域；表示发动机工作在可行域内的的耗油率；，分别为仿真工况的开始、结束时间。

       系统的状态方程同式(3)。为了实现电池电量的可靠维持，一般要求电池SOC的终端值与初始值始终在一定范围之内，即目标函数可改为

(6)

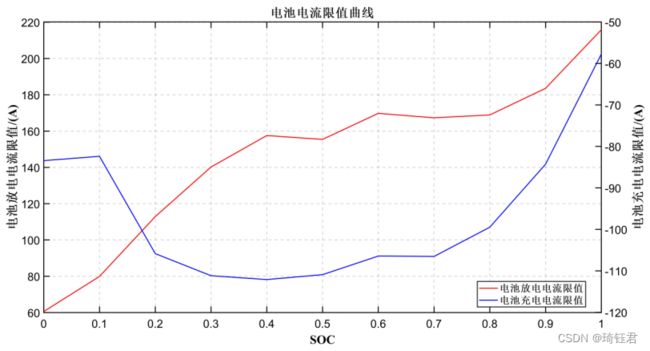
       同时，受制于各部件的实际工作能力，发动机、电机的输出转矩、转速和电池电流需满足一定的约束条件

 约束条件构成了控制变量的容许可达集，同时限制各部件工作在合理范围。

2.2 基于Pontryagin极小值原理控制策略的构建

       Pontryagin极小值原理是基于古典变分法推导得到的一种求解最优控制问题的经典方法。由Pontryagin极小值原理可知，最优控制输入[,] 必须使得系统的Hamiltonian函数取得最小值，即

	(7)
	(8)

       同时，需满足系统正则方程

(9)

式中为协同状态变量。由于的初始值未知，通常采用迭代搜索的方法来求解最优值。

2.3 基于Pontryagin极小值原理控制策略求解

       综上所述，利用极小值原理可对能量控制策略的目标函数进行求解。能量优化控制策略的意义是以获得一个最佳控制变量  、使燃油消耗最小，采用极小值原理的具体形式可表示为

(10)

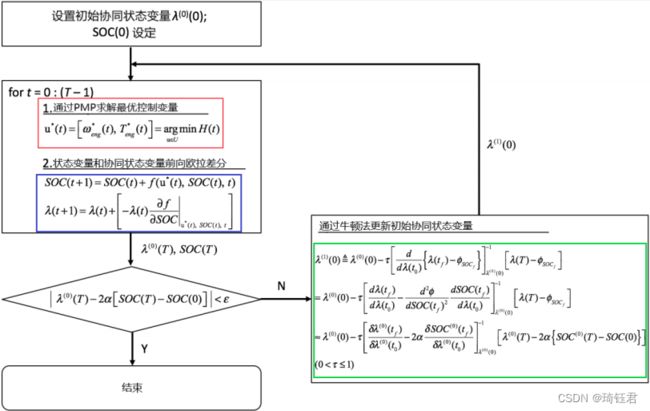
       对于这种两点边界值的求解问题，采用循环迭代选取初始值过程的方法，获得全局最优控制策略和电池能量状态满足的条件。总体求解流程如图8所示，具体过程如下。

图8 PMP求解能量管理流程图

        (1)  在每一个时刻里，为了找到使哈密顿函数最小的控制变量，我们将发动机速度-扭矩平面(控制平面)上的可行区域离散为发动机扭矩和速度分辨率分别为1(Nm)和1(rad/s)的网格。然后，我们检查网格中每个点的可行性，并计算每个可行点的哈密顿量，最小哈密顿量对应于最优控制的可行点。

        (2) 应用上述所获得的最佳控制变量，在系统状态约束的范围内采用式(9)系统动态方程和协态方程计算相应的数值，直至整个循环工况结束，然后计算并与进行比较：，如果在此范围内，则循环结束；否则采用射击打靶法重新选取，直到符合： 。

3 仿真实验及结果分析

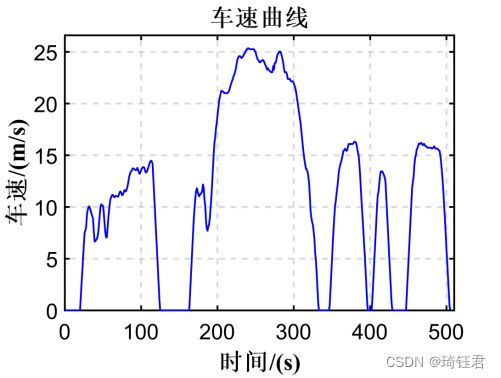
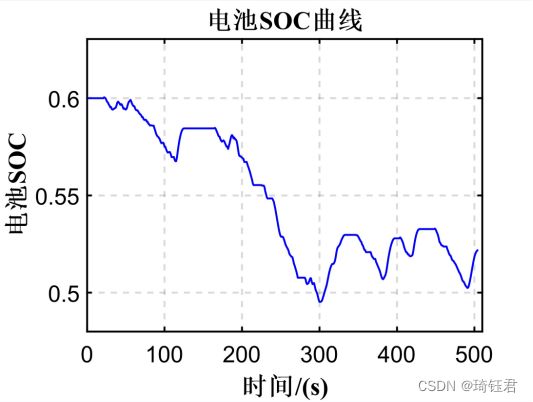
        为验证基于极小值原理的能量控制策略的优化效果，根据图1和图8分别建立系统(发动机、电机MG1、电机MG2、动力电池)数值模型和编写控制优化程序，以典型循环工况为例进行仿真实验，设定电池SOC初始值为0.6。

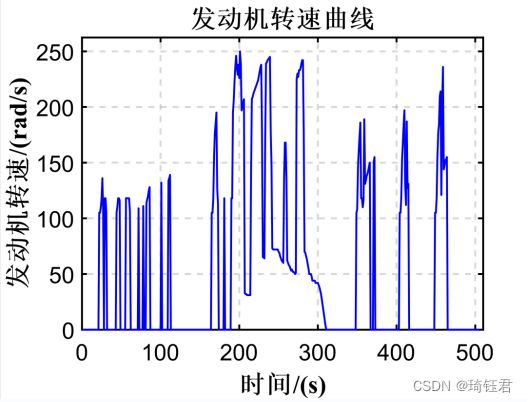
        图9为选取的随机工况，包括车速随时间的变化曲线。由车速曲线可知，整个过程中包括了起动、加速、急加速和减速等阶段。图10 为在此随机工况下发动机输出转矩的仿真值。图11为在随机工况下发动机的输出转速的仿真值。图12为在此随机工况下电池SOC的仿真值。

图9 随机工况-车速-时间变化曲线

图10 发动机转矩曲线

图11 发动机转速曲线

图12 电池SOC运动轨迹

      由图9-12可见，发动机工作点基本处于经济区域，电池SOC保持在一定的范围之内。

4 结论

       以提高功率分流式混合动力汽车燃油经济性为目标，根据该系统结构特点和对控制策略的适应性要求，设计了以发动机转矩和转速为控制变量，并基于极小值原理对能量控制策略进行了优化。根据极小值原理的求解流程建立仿真模型，结果表明: 采用极小值原理对功率分配是正确的，且对控制策略的优化是有效的。其具体表现为: 电池能量状态的平衡、发动机运行在高效区域内，以及燃油经济性较好。