【序列召回推荐】(task5)多兴趣召回Comirec-DR

note：

• 多兴趣召回建模。Comirec论文中的提出的第一个模型：Comirec-DR（DR就是dynamic routing），阿里将用户行为序列的item embeddings作为初始的capsule，然后提取出多个兴趣capsules，即为用户的多个兴趣。其中胶囊网络中的动态路由算法是原始的dynamic routing（CapsNet），和MIND动态路由的两大不同点：
  • 输入序列胶囊$i$与所产生的兴趣胶囊 $j$ 的权重 $b_{ij}$初始化为0；
  • 在Comirec-DR中对于不同的序列胶囊i与兴趣胶囊j，我们都有一个独立的$W_{ij}\in {\mathbb{R}}^{d\times d}$来完成序列胶囊i到兴趣胶囊j之间的映射。
• 原论文是按照8:1:1划分训练集、验证集、测试集（按照用户划分，更具泛化能力）。
  • 训练样本：全部点击序列$\left(e_1^{(u)},e_2^{(u)},\dots ,e_k^{(u)},\dots ,e_n^{(u)}\right)$，用前（n-1）个item预测第n个；
  • 验证集合测试集则是使用用户前80%的点击序列作为模型输入，然后预测后面的点击序列。

一、Comirec模型概览

Comirec：Controllable Multi-Interest Framework for Recommendation
论文链接：https://arxiv.org/abs/2005.09347

Comirec是阿里发表在KDD 2020上的一篇工作，这篇论文对MIND多行为召回进行了扩展：

• 一方面改进了MIND中的动态路由算法，
• 另一方面提出了一种新的多兴趣召回方法，同时对推荐的多样性层面也做出了一定的贡献，通过一种贪心的做法，在损失较小的推荐效果的情况下可以显著的提高推荐的多样性(感觉非常非常牵强，我们这里就不介绍这个了)，从而极大的提高用户的使用体验，可以更进一步的探索用户的潜在兴趣。

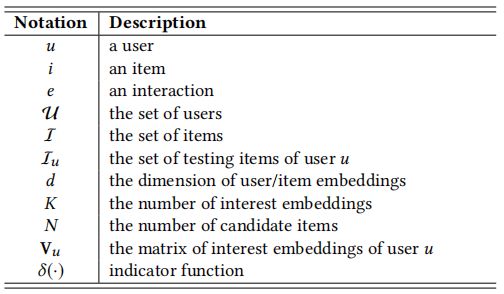
1.1 Notation

假设一个用户集合 $u\in \mathcal{U}$ 和一个物品集合 $i\in \mathcal{I}$, 对于每一个用户, 定义用户序列 $\left(e_1^{(u)},e_2^{(u)},\dots ,e_n^{(u)}\right)$, 根据时间先后顺序排序，其中$e_t^{(u)}$ 记录了第 $t$ 个物品与用户交互。

1.2 模型框架

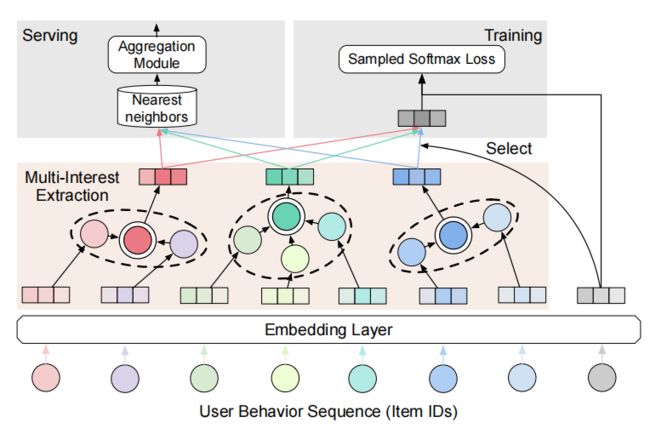
Comirec流程和MIND类似（区别更大是后面task6的Comirec-SR）：

• 用户历史交互item ids经过embedding layer转为item embeddings；
• 把刚才的item embedding经过多兴趣抽取层，得到K个interest embeddings；
• training：和之前MIND说的做法一样（取内积最大值），即选出与target item embedding最接近的interest embeddings，基于多分类任务，使用负采样sampled softmax loss；
• serving（predict）：对于每个用户的K个interest embedding进行top-N检索，即召回K X N个item。
• aggregation module：将K X N个item送入该模块得到N个item（选内积分数最高的N个，和MIND做法一致）：$$f(u,i)=\underset{1\le k\le K}{\max }\left({\mathbf{e}}_i^{\top }{\mathbf{v}}_u^{(k)}\right)$$

1.3 model training

和1.1说的一样，某用户经过多兴趣提取层后得到K个interest embeddings后，从中找出和target item i（即下面embedding为$e_i$）最接近，即内积最大的一个interest embeeding，方法如下$${\mathbf{v}}_u={\mathbf{V}}_u\left[:,\mathrm{argmax}\left({\mathbf{V}}_u^{\top }{\mathbf{e}}_i\right)\right],$$
和之前一样是结合负采样的最大似然法（后面代码用少量数据，直接交叉熵损失函数）。给出一个训练样本 $(u,i)$, 用户embedding ${\mathbf{v}}_u$, 和物品embedding ${\mathbf{e}}_i$，则用户与物品交互的似然函数：
$$P_{\theta }(i\mid u)=\frac{\exp \left({\mathbf{v}}_u^{\top }{\mathbf{e}}_i\right)}{{\sum }_{k\in I}\exp \left({\mathbf{v}}_u^{\top }{\mathbf{e}}_k\right)}$$
目标为最小化该似然函数：
$$\text{ loss }=\sum _{u\in \mathcal{U}}\sum _{i\in I_u}-\log P_{\theta }(i\mid u)$$

二、Comirec-DR模型

2.1 数据集划分

原论文是按照8:1:1划分训练集、验证集、测试集（按照用户划分，更具泛化能力）。

• 训练样本：全部点击序列$\left(e_1^{(u)},e_2^{(u)},\dots ,e_k^{(u)},\dots ,e_n^{(u)}\right)$，用前（n-1）个item预测第n个；
• 验证集合测试集则是使用用户前80%的点击序列作为模型输入，然后预测后面的点击序列。

2.2 Comirec-DR中的动态路由

• primary capsules：用户行为序列的物品embedding
• interest capsules：多元用户兴趣

Comirec-DR和MIND一样都是使用胶囊网络中的Dynamic Routing算法进行多兴趣embedding的提取：

• 1.第一行对输入序列胶囊$i$ 与所产生的兴趣胶囊 $j$ 的权重 $b_{ij}$ 初始化为 0
• 2.第二行开始进行三次动态路由
• 3.第三行是对每一个序列胶囊i对应的所有兴趣胶囊j的权重$\left\{b_{ij},j=1,\dots ,K\right\}$进行Softmax归一化
• 4.第四行是对每一个兴趣胶囊j对应所有的序列胶囊i执行第四行中的计算
  • 注意：$W_{ij}\in {\mathbb{R}}^{d\times d}$为序列胶囊i到兴趣胶囊j的映射矩阵（即转换矩阵，MIND中是使用同一个矩阵），这样就完成了对序列到单个兴趣胶囊的特征提取，以此类推我们可以得到所有的兴趣胶囊
  • $c_{ij}$ 为「耦合系数」(coupling coefficients), 由迭代动态路由过程确定
• 5.对4中得到的兴趣胶囊的表征通过squash激活函数激活
  $$\mathrm{squash}\left(z_j\right)=\frac{{\Vert z_j\Vert }^2}{1+{\Vert z_j\Vert }^2}\frac{z_j}{\Vert z_j\Vert }$$
• 6.最后我们通过第6行中的公式来更新 $b_{ij}$（注意不是像NN一样通过反向传播更新参数）
• 7.至此就完成了一次动态路由, 我们将这个过程重复三次就得到了完整的动态路由, 也就完成了多兴趣表征的建模

2.3 Comirec-DR与MIND的异同

Comirec-DR与MIND的核心区别主要有两个:

• 1.输入序列胶囊$i$与所产生的兴趣胶囊 $j$ 的权重 $b_{ij}$ 的初始化方式不一样：
  • 在Comirec-DR中对 $b_{ij}$ 全部初始化为 0 ,
  • 在MIND中对 $b_{ij}$ 全部用高斯分布分布进行初始化的映射矩阵使用同一矩阵 $S\in {\mathbb{R}}^{d\times d}$
• 2.在进行序列胶囊与兴趣胶囊之间的映射转换时的变量声明方式不一样：
  • 在Comirec-DR中对于不同的序列胶囊i与兴趣胶囊j，我们都有一个独立的$W_{ij}\in {\mathbb{R}}^{d\times d}$来完成序列胶囊i到兴趣胶囊j之间的映射。
  • 在MIND中，其提出的B2I Dynamic Routing中将所有的序列胶囊i与兴趣胶囊j的映射矩阵使用同一矩阵$S\in {\mathbb{R}}^{d\times d}$。

三、代码实践

3.1 Capsule network定义

为了完成了对序列到单个兴趣胶囊的特征提取，将$W_{ij}\in {\mathbb{R}}^{d\times d}$作为序列胶囊i到兴趣胶囊j的映射矩阵（MIND中是使用同一个矩阵），即可学习的参数。以此类推我们可以得到所有的兴趣胶囊。所以下面改成self.create_parameter，如果可以用torch是用torch.nn.Parameter函数，可以理解为类型转化函数，将一个不可训练类型Tensor转为可以训练的parameter。

class CapsuleNetwork(nn.Layer):

    def __init__(self, hidden_size, seq_len, bilinear_type=2, interest_num=4, routing_times=3, hard_readout=True,
                 relu_layer=False):
        super(CapsuleNetwork, self).__init__()
        self.hidden_size = hidden_size  # h
        self.seq_len = seq_len  # s
        self.bilinear_type = bilinear_type
        self.interest_num = interest_num
        self.routing_times = routing_times
        self.hard_readout = hard_readout
        self.relu_layer = relu_layer
        self.stop_grad = True
        self.relu = nn.Sequential(
            nn.Linear(self.hidden_size, self.hidden_size, bias_attr=False),
            nn.ReLU()
        )
        if self.bilinear_type == 0:  # MIND
            self.linear = nn.Linear(self.hidden_size, self.hidden_size, bias_attr=False)
        elif self.bilinear_type == 1:
            self.linear = nn.Linear(self.hidden_size, self.hidden_size * self.interest_num, bias_attr=False)
        else:  # ComiRec_DR
            self.w = self.create_parameter(
                shape=[1, self.seq_len, self.interest_num * self.hidden_size, self.hidden_size])

    def forward(self, item_eb, mask):
        if self.bilinear_type == 0:  # MIND
            item_eb_hat = self.linear(item_eb)  # [b, s, h]
            item_eb_hat = paddle.repeat_interleave(item_eb_hat, self.interest_num, 2) # [b, s, h*in]
        elif self.bilinear_type == 1:
            item_eb_hat = self.linear(item_eb)
        else:  # ComiRec_DR
            u = paddle.unsqueeze(item_eb, 2)  # shape=(batch_size, maxlen, 1, embedding_dim)
            item_eb_hat = paddle.sum(self.w[:, :self.seq_len, :, :] * u,
                                    3)  # shape=(batch_size, maxlen, hidden_size*interest_num)

        item_eb_hat = paddle.reshape(item_eb_hat, (-1, self.seq_len, self.interest_num, self.hidden_size))
        item_eb_hat = paddle.transpose(item_eb_hat, perm=[0,2,1,3])
        # item_eb_hat = paddle.reshape(item_eb_hat, (-1, self.interest_num, self.seq_len, self.hidden_size))

        # [b, in, s, h]
        if self.stop_grad:  # 截断反向传播，item_emb_hat不计入梯度计算中
            item_eb_hat_iter = item_eb_hat.detach()
        else:
            item_eb_hat_iter = item_eb_hat

        # b的shape=(b, in, s)
        if self.bilinear_type > 0:  # b初始化为0（一般的胶囊网络算法）
            capsule_weight = paddle.zeros((item_eb_hat.shape[0], self.interest_num, self.seq_len))
        else:  # MIND使用高斯分布随机初始化b
            capsule_weight = paddle.randn((item_eb_hat.shape[0], self.interest_num, self.seq_len))

        for i in range(self.routing_times):  # 动态路由传播3次
            atten_mask = paddle.repeat_interleave(paddle.unsqueeze(mask, 1), self.interest_num, 1) # [b, in, s]
            paddings = paddle.zeros_like(atten_mask)

            # 计算c，进行mask，最后shape=[b, in, 1, s]
            capsule_softmax_weight = F.softmax(capsule_weight, axis=-1)
            capsule_softmax_weight = paddle.where(atten_mask==0, paddings, capsule_softmax_weight)  # mask
            capsule_softmax_weight = paddle.unsqueeze(capsule_softmax_weight, 2)

            if i < 2:
                # s=c*u_hat , (batch_size, interest_num, 1, seq_len) * (batch_size, interest_num, seq_len, hidden_size)
                interest_capsule = paddle.matmul(capsule_softmax_weight,
                                                item_eb_hat_iter)  # shape=(batch_size, interest_num, 1, hidden_size)
                cap_norm = paddle.sum(paddle.square(interest_capsule), -1, keepdim=True)  # shape=(batch_size, interest_num, 1, 1)
                scalar_factor = cap_norm / (1 + cap_norm) / paddle.sqrt(cap_norm + 1e-9)  # shape同上
                interest_capsule = scalar_factor * interest_capsule  # squash(s)->v,shape=(batch_size, interest_num, 1, hidden_size)

                # 更新b
                delta_weight = paddle.matmul(item_eb_hat_iter,  # shape=(batch_size, interest_num, seq_len, hidden_size)
                                            paddle.transpose(interest_capsule, perm=[0,1,3,2])
                                            # shape=(batch_size, interest_num, hidden_size, 1)
                                            )  # u_hat*v, shape=(batch_size, interest_num, seq_len, 1)
                delta_weight = paddle.reshape(delta_weight, (
                -1, self.interest_num, self.seq_len))  # shape=(batch_size, interest_num, seq_len)
                capsule_weight = capsule_weight + delta_weight  # 更新b
            else:
                interest_capsule = paddle.matmul(capsule_softmax_weight, item_eb_hat)
                cap_norm = paddle.sum(paddle.square(interest_capsule), -1, keepdim=True)
                scalar_factor = cap_norm / (1 + cap_norm) / paddle.sqrt(cap_norm + 1e-9)
                interest_capsule = scalar_factor * interest_capsule

        interest_capsule = paddle.reshape(interest_capsule, (-1, self.interest_num, self.hidden_size))

        if self.relu_layer:  # MIND模型使用book数据库时，使用relu_layer
            interest_capsule = self.relu(interest_capsule)

        return interest_capsule

3.2 Comirec-DR类定义

下面其实和MIND一样的，改动的都在CapsuleNetwork体现出来的。

class ComirecDR(nn.Layer):
    def __init__(self, config):
        super(ComirecDR, self).__init__()

        self.config = config
        self.embedding_dim = self.config['embedding_dim']
        self.max_length = self.config['max_length']
        self.n_items = self.config['n_items']

        self.item_emb = nn.Embedding(self.n_items, self.embedding_dim, padding_idx=0)
        self.capsule = CapsuleNetwork(self.embedding_dim, self.max_length, bilinear_type=2,
                                      interest_num=self.config['K'])
        self.loss_fun = nn.CrossEntropyLoss()
        self.reset_parameters()

    def calculate_loss(self,user_emb,pos_item):
        all_items = self.item_emb.weight
        scores = paddle.matmul(user_emb, all_items.transpose([1, 0]))
        return self.loss_fun(scores,pos_item)

    def output_items(self):
        return self.item_emb.weight

    def reset_parameters(self, initializer=None):
        for weight in self.parameters():
            paddle.nn.initializer.KaimingNormal(weight)

    def forward(self, item_seq, mask, item, train=True):

        if train:
            seq_emb = self.item_emb(item_seq)  # Batch,Seq,Emb
            item_e = self.item_emb(item).squeeze(1)

            multi_interest_emb = self.capsule(seq_emb, mask)  # Batch,K,Emb

            cos_res = paddle.bmm(multi_interest_emb, item_e.squeeze(1).unsqueeze(-1))
            k_index = paddle.argmax(cos_res, axis=1)

            best_interest_emb = paddle.rand((multi_interest_emb.shape[0], multi_interest_emb.shape[2]))
            for k in range(multi_interest_emb.shape[0]):
                best_interest_emb[k, :] = multi_interest_emb[k, k_index[k], :]

            loss = self.calculate_loss(best_interest_emb,item)
            output_dict = {
                'user_emb': multi_interest_emb,
                'loss': loss,
            }
        else:
            seq_emb = self.item_emb(item_seq)  # Batch,Seq,Emb
            multi_interest_emb = self.capsule(seq_emb, mask)  # Batch,K,Emb
            output_dict = {
                'user_emb': multi_interest_emb,
            }
        return output_dict

3.3 基于Faiss的向量召回

这里的最近邻就和之前task有点不同，因为是多兴趣评估，要num_interest个兴趣向量的所有topN近邻物品（num_interest*topN个物品）集合起来按照距离重新排序。

def get_predict(model, test_data, hidden_size, topN=20):

    item_embs = model.output_items().cpu().detach().numpy()
    item_embs = normalize(item_embs, norm='l2')
    gpu_index = faiss.IndexFlatIP(hidden_size)
    gpu_index.add(item_embs)
    
    test_gd = dict()
    preds = dict()
    
    user_id = 0

    for (item_seq, mask, targets) in tqdm(test_data):

        # 获取用户嵌入
        # 多兴趣模型，shape=(batch_size, num_interest, embedding_dim)
        # 其他模型，shape=(batch_size, embedding_dim)
        user_embs = model(item_seq,mask,None,train=False)['user_emb']
        user_embs = user_embs.cpu().detach().numpy()

        # 用内积来近邻搜索，实际是内积的值越大，向量越近（越相似）
        if len(user_embs.shape) == 2:  # 非多兴趣模型评估
            user_embs = normalize(user_embs, norm='l2').astype('float32')
            D, I = gpu_index.search(user_embs, topN)  # Inner Product近邻搜索，D为distance，I是index
#             D,I = faiss.knn(user_embs, item_embs, topN,metric=faiss.METRIC_INNER_PRODUCT)
            for i, iid_list in enumerate(targets):  # 每个用户的label列表，此处item_id为一个二维list，验证和测试是多label的
                test_gd[user_id] = iid_list
                preds[user_id] = I[i,:]
                user_id +=1
        else:  # 多兴趣模型评估
            ni = user_embs.shape[1]  # num_interest
            user_embs = np.reshape(user_embs,
                                   [-1, user_embs.shape[-1]])  # shape=(batch_size*num_interest, embedding_dim)
            user_embs = normalize(user_embs, norm='l2').astype('float32')
            D, I = gpu_index.search(user_embs, topN)  # Inner Product近邻搜索，D为distance，I是index
#             D,I = faiss.knn(user_embs, item_embs, topN,metric=faiss.METRIC_INNER_PRODUCT)
            for i, iid_list in enumerate(targets):  # 每个用户的label列表，此处item_id为一个二维list，验证和测试是多label的
                recall = 0
                dcg = 0.0
                item_list_set = []

                # 将num_interest个兴趣向量的所有topN近邻物品（num_interest*topN个物品）集合起来按照距离重新排序
                item_list = list(
                    zip(np.reshape(I[i * ni:(i + 1) * ni], -1), np.reshape(D[i * ni:(i + 1) * ni], -1)))
                item_list.sort(key=lambda x: x[1], reverse=True)  # 降序排序，内积越大，向量越近
                for j in range(len(item_list)):  # 按距离由近到远遍历推荐物品列表，最后选出最近的topN个物品作为最终的推荐物品
                    if item_list[j][0] not in item_list_set and item_list[j][0] != 0:
                        item_list_set.append(item_list[j][0])
                        if len(item_list_set) >= topN:
                            break
                test_gd[user_id] = iid_list
                preds[user_id] = item_list_set
                user_id +=1
    return test_gd, preds

def evaluate(preds,test_gd, topN=50):
    total_recall = 0.0
    total_ndcg = 0.0
    total_hitrate = 0
    for user in test_gd.keys():
        recall = 0
        dcg = 0.0
        item_list = test_gd[user]
        for no, item_id in enumerate(item_list):
            if item_id in preds[user][:topN]:
                recall += 1
                dcg += 1.0 / math.log(no+2, 2)
            idcg = 0.0
            for no in range(recall):
                idcg += 1.0 / math.log(no+2, 2)
        total_recall += recall * 1.0 / len(item_list)
        if recall > 0:
            total_ndcg += dcg / idcg
            total_hitrate += 1
    total = len(test_gd)
    recall = total_recall / total
    ndcg = total_ndcg / total
    hitrate = total_hitrate * 1.0 / total
    return {f'recall@{topN}': recall, f'ndcg@{topN}': ndcg, f'hitrate@{topN}': hitrate}

# 指标计算
def evaluate_model(model, test_loader, embedding_dim,topN=20):
    test_gd, preds = get_predict(model, test_loader, embedding_dim, topN=topN)
    return evaluate(preds, test_gd, topN=topN)

时间安排

任务信息	截止时间	完成情况
11月14日周一正式开始
Task01：Paddle开发深度学习模型快速入门	11月14、15、16日周三	完成
Task02：传统序列召回实践：GRU4Rec	11月17、18、19日周六	完成
Task03：GNN在召回中的应用：SR-GNN	11月20、21、22日周二	完成
Task04：多兴趣召回实践：MIND	11月23、24、25、26日周六	完成
Task05：多兴趣召回实践：Comirec-DR	11月27、28日周一	完成
Task06：多兴趣召回实践：Comirec-SA	11月29日周二

Reference

[1] 多兴趣召回实践：Comirec-DR
论文：Controllable Multi-Interest Framework for Recommendation
链接：https://arxiv.org/abs/2005.09347
tensorflow代码1；Pytorch代码2
[2] 多兴趣召回实践：Comirec-SA
论文：Controllable Multi-Interest Framework for Recommendation
链接：https://arxiv.org/abs/2005.09347
代码1：https://github.com/THUDM/ComiRec/blob/a576eed8b605a531f2971136ce6ae87739d47693/src/model.py
代码2：https://github.com/ShiningCosmos/pytorch_ComiRec/blob/main/ComiRec.py
[3] 推荐场景中召回模型的演化过程. 京东大佬
[4] 推荐系统论文阅读（四十三)-Comirec：阿里又一篇多兴趣召回的论文
[5] 多兴趣推荐召回模型：ComiRec
[6] ComiRec-DR和MIND中Dynamic Routing的差异
[7] KDD2020｜阿里团队最新的多元兴趣推荐模型—ComiRec
[8] Yukuo Cen, Xu Zou, Jianwei Zhang, Hongxia Yang, Jingren Zhou, and Jie Tang.2019. Representation learning for attributed multiplex heterogeneous network. In KDD’19. 1358–1368.
[9] Sara Sabour, Nicholas Frosst, and Geoffrey E Hinton. 2017. Dynamic routing between capsules. In NIPS’17. 3856–3866.