基于python利用statsmodels实现一元线性回归、高阶回归以及自变量为分类变量的回归（逐行代码解读，超细节）

一元线性回归

#导入要用的包，没有下载包的要用pip install安装对应的包
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

nsample = 20 #定义样本量
x = np.linspace(0, 10, nsample) #生成0-10之间的20个数，作为样本
x

array([ 0.        ,  0.52631579,  1.05263158,  1.57894737,  2.10526316,
        2.63157895,  3.15789474,  3.68421053,  4.21052632,  4.73684211,
        5.26315789,  5.78947368,  6.31578947,  6.84210526,  7.36842105,
        7.89473684,  8.42105263,  8.94736842,  9.47368421, 10.        ])

X = sm.add_constant(x) #增加一列，默认值为1
X #此时X是20*2的矩阵了

array([[ 1.        ,  0.        ],
       [ 1.        ,  0.52631579],
       [ 1.        ,  1.05263158],
       [ 1.        ,  1.57894737],
       [ 1.        ,  2.10526316],
       [ 1.        ,  2.63157895],
       [ 1.        ,  3.15789474],
       [ 1.        ,  3.68421053],
       [ 1.        ,  4.21052632],
       [ 1.        ,  4.73684211],
       [ 1.        ,  5.26315789],
       [ 1.        ,  5.78947368],
       [ 1.        ,  6.31578947],
       [ 1.        ,  6.84210526],
       [ 1.        ,  7.36842105],
       [ 1.        ,  7.89473684],
       [ 1.        ,  8.42105263],
       [ 1.        ,  8.94736842],
       [ 1.        ,  9.47368421],
       [ 1.        , 10.        ]])

#β0,β1分别设置成2,5
beta = np.array([2, 5]) #beta 是2*1的
beta

array([2, 5])

#生成误差项
e = np.random.normal(size=nsample) #生成一组误差项，生成高斯噪声数据20个
e

array([-0.42047181, -0.85236665, -0.68113011,  0.36979962,  0.99786982,
       -1.45427248,  1.30999087, -2.13065843,  1.03693165, -0.40551066,
       -0.7215544 , -2.88139423,  1.03241744,  0.35218758, -0.46994703,
       -0.37775266, -0.29225747, -1.75429756,  0.02519833, -2.1975942 ])

#利用实际值y
y = np.dot(X, beta) + e #dot是用来算矩阵内积的，20*2 2*1 -> 20*1，接着添加高斯噪声，产生模拟用的数据
y #y是20*1的矩阵

array([ 1.57952819,  3.77921229,  6.58202779, 10.26453647, 13.52418561,
       13.70362226, 19.09946456, 18.2903942 , 24.08956323, 25.27869987,
       27.59423507, 28.06597419, 34.61136481, 36.56271389, 38.37215823,
       41.09593155, 43.81300569, 44.98254455, 49.39361938, 49.8024058 ])

#调用statsmodels中的方法OLS实现最小二乘法
model = sm.OLS(y,X) #sm.OLS最小二乘，返回一个model

#拟合数据
res = model.fit() #fit就是拟合数据

#回归系数
res.params #params查看拟合出的回归系数，对比设计的系数2,5，还是有一定的误差，这与数据的随机性有关

#全部结果
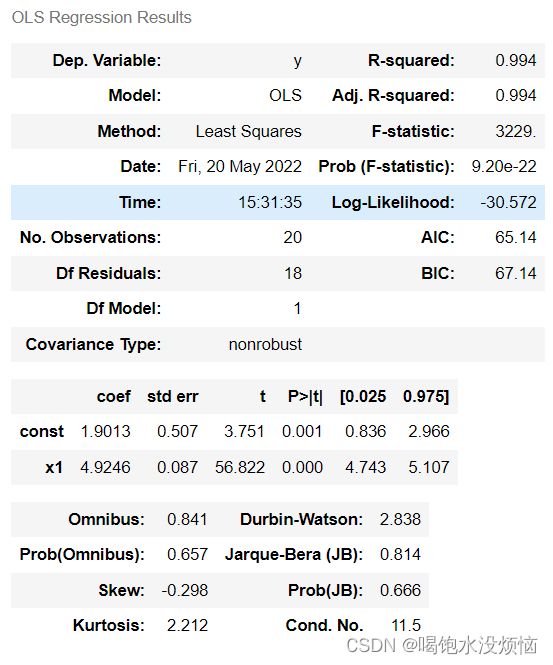
res.summary() #summary()返回全部结果

 R2是0.994，因为是一元线性回归，所以调整后的R2也是0.994，另外t统计量的p值也接近于0，拟合效果还是很不错的。

#拟合的估计值
y_ = res.fittedvalues
y_

array([ 1.90128908,  4.49318069,  7.0850723 ,  9.67696391, 12.26885552,
       14.86074713, 17.45263874, 20.04453036, 22.63642197, 25.22831358,
       27.82020519, 30.4120968 , 33.00398841, 35.59588002, 38.18777163,
       40.77966324, 43.37155485, 45.96344646, 48.55533807, 51.14722968])

fig, ax = plt.subplots(figsize=(8,6)) #设置画布
ax.plot(x, y, 'o', label='data') #原始数据
ax.plot(x, y_, 'r--.',label='test') #拟合数据
ax.legend(loc='best') #展示图例
plt.show()

 绘图可以看出，回归线很好地拟合了数据点。这是一元线性回归的情况，高阶回归可以看下一篇。

高阶回归建模（二次多项式转二元线性回归）

#导入需要用的数据包，没有下载依赖包的，可以到Anaconda命令窗口，或者cmd中通关pip install进行下载安装
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

#Y=5+2⋅X+3⋅X^2
 
nsample = 50 #定义样本量
x = np.linspace(0, 10, nsample) #生成以0为开头，以10为结尾的nsample个等差数据
X = np.column_stack((x, x**2)) #按照需求去添加一列x平方，这样就有x和x平方这2列数据了
X = sm.add_constant(X) #再添加一个全为1的列

beta = np.array([5, 2, 3]) #定义回归系数咯
e = np.random.normal(size=nsample) #来生成size为nsample个的高斯噪声
y = np.dot(X, beta) + e #通过计算矩阵的点乘内积，再加上高斯噪声的方式，生成需要用的模拟数据
model = sm.OLS(y,X) #利用模拟数据的因变量y与自变量们(1,x,x^2)进行最小二乘回归，返回model
results = model.fit() #拟合数据，返回拟合结果啦
results.params #查看拟合出的回归系数

array([4.38991842, 2.38291522, 2.9591748 ])

可以看出和设定的系数5，2，3还是接近的，但是也有一定的误差。

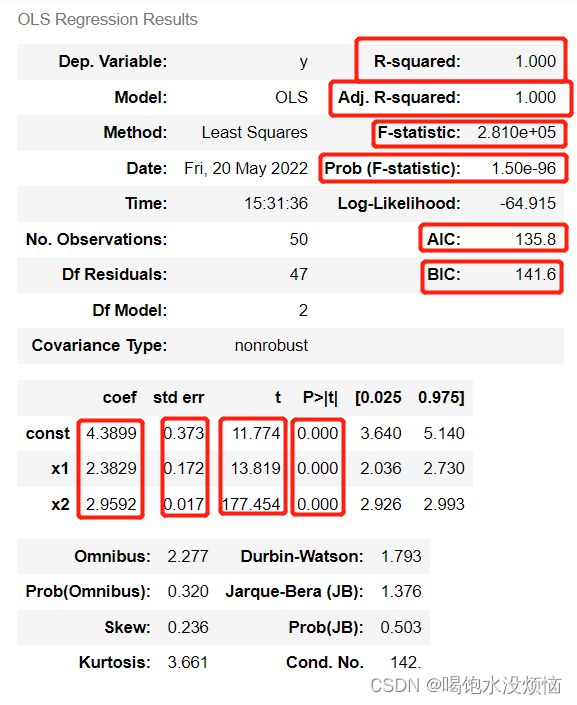
results.summary() #查看拟合结果分析

 下面来逐一解读这些指标的含义与作用，R2称为拟合优度或可决系数，它代表的是回归方程对数据的拟合效果，下面的Adj. R-squared指的是调整后的R2，它是为了解决“多元线性回归中，残差平方和会随着自由度的增加而减少，至少不会增加。”这一问题引入的。

其中n-k就是残差平方和的自由度，可以理解为，分子分母各除以自己的自由度，这样就修正了自由度造成的残差平方和变小，进而R2自动变大的问题。

下面的是F统计量，它代表的是回归方程的整体拟合效果的好坏，可以用它与F统计量的临界值对比，但一般我们直接看其P值，效果也是一样的，显然该P值达到了10的-96次方，很小很小，认为可以拒绝原假设了，也就是模型拟合较好的意思。

AIC与BIC值也可以用来作为模型拟合好坏的参考，一般选择AIC或BIC更小的模型。

下面的coef指的是回归系数了，const显然是截距项或常数项，另外两个是自变量，后面的std err叫学生化残差，显然也是越小越好，后面的t统计量是用来衡量每个自变量是否显著的，也就是这个自变量有没有对因变量有比较大的影响，它也是要与人为设置的临界值进行比较，这里不再赘述，我们可以直接看后面的p值，p值一般小于0.05就认为有效了，这里都接近于0了，可以看出来每个自变量都显著。

y_fitted = results.fittedvalues #给出y的拟合值
fig, ax = plt.subplots(figsize=(8,6)) #绘制画布
ax.plot(x, y, 'o', label='data') #绘制原始数据的图
ax.plot(x, y_fitted, 'r--.',label='OLS') #绘制拟合数据图
ax.legend(loc='best') #生成图例
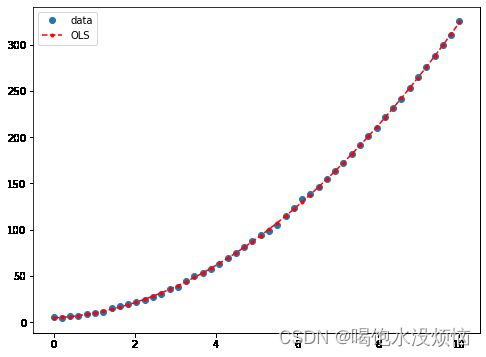
plt.show()

 来绘个图看看效果吧

这就是抛物线，也就是二次多项式的图像了，同样的三次多项式，甚至指数型和对数型也可以通过对应的数据处理化简为高阶线性回归的形式进行拟合哦。 

实现自变量为分类变量的回归

 假设分类变量有3个取值（a,b,c）,比如考试成绩有3个等级。那么a就是（1,0,0），b（0,1,0），c(0,0,1),这个时候就需要3个系数β0,β1,β2，也就是

#导入需要用的数据包，没有下载依赖包的，可以到Anaconda命令窗口，或者cmd中通关pip install进行下载安装
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

nsample = 50
groups = np.zeros(nsample,int) #构造一个元素数量为50的int型0向量

groups[20:40] = 1 #将groups中20:40的数据改成1
groups[40:] = 2 #将groups中40之后的数据改成2
dummy = sm.categorical(groups, drop=True) #将groups设置成categorical格式，也就是按照取值，比如0就设成[1.,0.,0.]，1就设成[0.,1.,0.]，2就设成[0.,0.,1.]

#Y=5+2X+3Z1+6⋅Z2+9⋅Z3.

x = np.linspace(0, 20, nsample) #生成nsample个0-20的等差数列数据咯
X = np.column_stack((x, dummy)) #将x与dummy合并到一起，显然x只是1列，而dummy有3列，这样子合并起来就有4列啦
X = sm.add_constant(X) #再在最左边添加一个全为1的列
beta = [5, 2, 3, 6, 9] #生成回归系数
e = np.random.normal(size=nsample) #生成nsample个高斯噪声
y = np.dot(X, beta) + e #生成模拟数据
result = sm.OLS(y,X).fit() #OLS进行最小二乘回归，然后会返回一个model对象，调用它的fit()方法，拟合数据，返回拟合结果
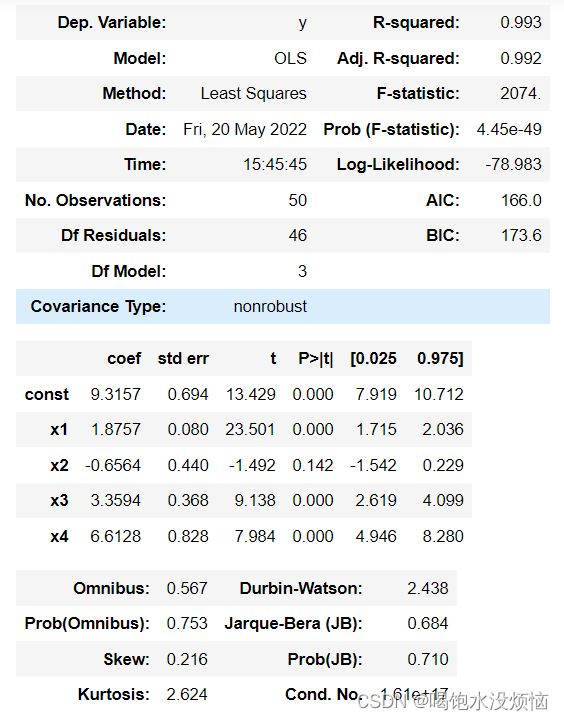
result.summary() #查看拟合结果

 调整后的R2为0.992，拟合的效果还可以。

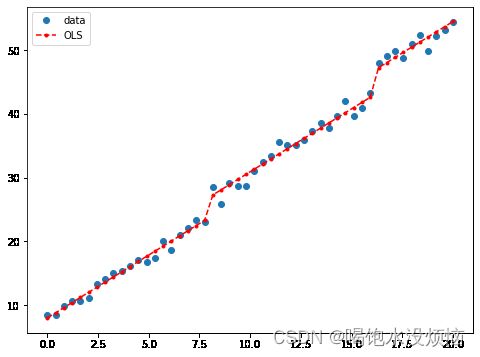
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, y, 'o', label="data")
ax.plot(x, result.fittedvalues, 'r--.', label="OLS")
ax.legend(loc='best') #添加图例
plt.show()

画个图瞅一眼：

嗯，图上看，拟合的也挺好的哈哈，随手写的，有问题可以私信我一起探讨，希望大佬们指导。