AB测试的介绍与实施

什么是AB测试

AB测试是为Web或App界面或流程制作两个（A/B）或多个（A/B/n）版本，在同一时间维度，分别让组成成分相同（相似）的访客群组（目标人群）随机的访问这些版本，收集各群组的用户体验数据和业务数据，最后分析、评估出最好版本，正式采用。（百度百科：https://baike.baidu.com/item/AB%E6%B5%8B%E8%AF%95/9231223?fr=aladdin）
简而言之，就是同时进行多个方案的测试，在这些方案中选出最好的版本，即寻求局部最优解。

AB测试的适用场景

适用场景	例子	不适用场景	例子
更优问题	ABC三种营销页哪个更好？	最优问题	如何设计最好的落地页？
估计短期影响	发送优惠券对于销量的提升	长期影响	新功能能否带来长期的收益？
因果分析	优化营销页能否提升转化率？	结果分析	转化率提升的原因？
战术性迭代	聊天按钮放在左边还是右边？	战略性迭代	要不要增加开聊按钮？

AB测试的原理

AB测试最核心的原理，就是假设检验，通过检验我们提出的假设是否正确来做出决策。对应到AB测试中，就是检验实验组&对照组，指标是否有显著差异。

AB测试的步骤

①确定需要做AB测试的业务及测试人群
②设计两种或多种测试方案
③提出假设，并设置原假设和备择假设
④确定观察指标
⑤计算最小样本量
⑥确定分流量和实验周期
⑦上线流量选择、时间设置
⑧实验策略上线
⑨实验结果评估（z/t 统计量检验、P值检验）

AB测试具体如何实施

①确定需要做AB测试的业务及测试人群

通常根据业务实际发展而定，比如页面优化、新功能的上线等，进行AB测试的业务及测试人群需与业务方沟通确定。

②设计两种或多种实验方案

根据沟通结果实际两组和多组实验方案，规划不同对照组、实验组实施的策略，预设实验结果可输出的对比效果。

③提出假设，并设置原假设和备择假设

原假设H0：μ1=μ2
备择假设H1：μ1≠μ2
通常将希望得到或证明的结果放备择假设

④确定观察指标

方案确定后续确定实验观察的指标。
核心指标：即业务想要提升的目标指标，通常一个，最多不超过3个，一般是均值或是比率。
基础指标：与基础体验相关的指标，比如优化营销页到商品选择页的转化率，在优化营销页的时候需保证新老版本的加载是一样。

⑤计算最小样本量

观察指标通常有两种类型，一种为均值类 如人均搜索次数，一种是比率 类比如用户的购买率、点击转化率等，两种类型计算最小样本量的方式有差异。最小样本量可以通过专业网站计算，也可使用python对应统计包中的函数计算。
1、均值类

均值类观察指标最小样本量计算网站：http://powerandsamplesize.com/Calculators/Compare-2-Means/2-Sample-Equality?
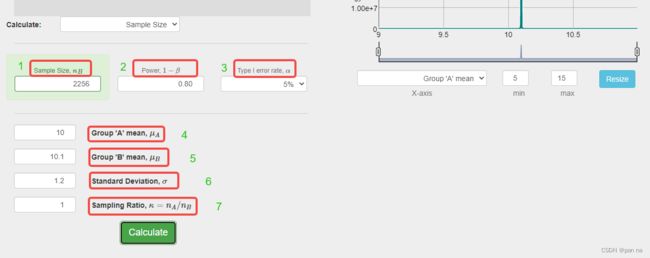
示例：
1处：估计的最小样本量；
2处： 1-β，常用0.8；
3处： α，常用5%；
4处：原始的均值，如均值是10；
5处：希望提升达到的均值，这里希望均值提升10%到达10.1；
6处：样本的标准差，取一段时间的样本计算标准差1.2
7处：两组实验分流量的比例，我们这里也是给到实验组和对照组样本量一样，所以两个样本的比例是1

2、比率类

比率类观察指标最小样本量计算网站：https://www.evanmiller.org/ab-testing/sample-size.html
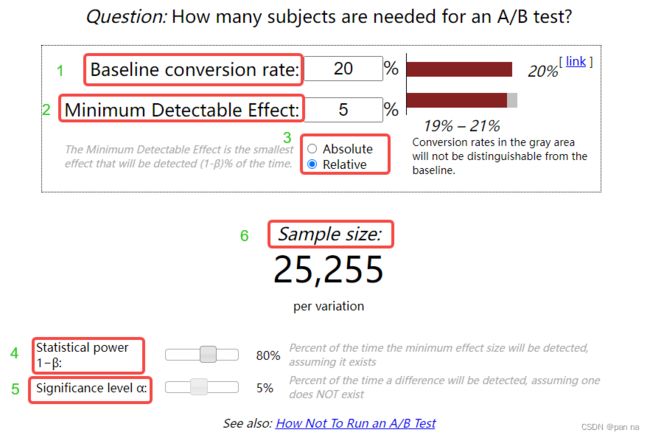
示例：
1处：原始比率，这里原始转化率是20%
2处：想提升的百分数，这个地方是根据3处的选项来填写具体的值
3处：提升的是绝对量还是涨幅，有两个选项Absolute是绝对量，Relative相对量（涨幅）。比如我想从20%提升到达21%。那么这里的2处填写5，3处选择Relative
4处：1-β常用80%
5处：α常用5%
6处：估计的最小样本量

⑥确定分流量和实验周期

测试的对照组和实验组都需达到最小样本量的需求，实验周期=最小样本量/单位时间内样本量。此处需注意特殊情况，如节假日、周末时用户量较多的影响。
为了排查因对照、实验组选取样本的差异对结果产生的影响，可在正式上策略之前空跑一段时间进行AA实验，如果数据差异显著，数据不可用需重新选组，如果数据差异不显著，记录两组之间的均值差，然后在实验期（AB两组实验条件不同）结束时，用实验期的组间差异，减去空跑期的组间差异，得到因策略带来的变化值。

⑦上线流量选择、时间设置

根据目标实验人群的特点选择策略上线的实验对象，设置实验空跑、上策略实验的时间。

⑧实验策略上线

⑨实验结果评估

实验结果是否显著可通过检验统计量或计算P值来判断。
检验统计量评估
在可接受置信水平下有对应的置信区间，计算样本Z/t检验统计量，观察检验统计量是否落在置信区间内，若未在置信区间内则认为有理由拒绝原假设接受备择假设，若在置信区间内则认为没有理由拒绝原假设。
P值检验评估
计算P值，即当原假设成立时，观测到样本数据出现的概率。统计学上，将5%作为一个小概率事件发生的概率，所以一般用5%来对比计算出来的P值。当P值小于5%时，认为原假设事件不可能发生，拒绝原假设接受备择假设；反之，当P值大于5%时，接受原假设。

eg：以下为利用构造的实验数据，结合python计算AB测试所需的最小样本量、实验结果检验。

1、均值类的检验

##均值的AB测试
###导包
import pandas as pd
import numpy as np
from scipy import stats
from statsmodels.stats.power import tt_ind_solve_power
from statsmodels.stats.proportion import proportion_effectsize as es 
from scipy.stats import ttest_ind,norm,f

##构建监测数据
data = {'avg_cnt':[11.077378,8.398665,8.571959,8.283145,5.93106,7.453807,9.184988,7.755004,8.438116,9.159712,6.773043,8.315689,7.682243,7.343689,8.982294,7.653003,7.419295,8.419876,6.440056,7.040037,9.724157,8.956077,8.760673,9.226514,6.82048,5.025931,6.90876,8.110434,6.430384,8.037746]}
df = pd.DataFrame(data)

###总体、样本正态性检验
##输出结果中第一个为统计量，第二个为P值（统计量越接近1越表明数据和正态分布拟合的好，P值大于指定的显著性水平，接受原假设，认为样本来自服从正态分布的总体）
print(stats.shapiro(df))

##输出结果中第一个为统计量，第二个为P值（注：p值大于显著性水平0.05，认为样本数据符合正态分布）
print(stats.normaltest(df))

##在计算样本量之前，计算样本均值和标准差
print("标准差：",np.std(df))
print("均值：",np.mean(df))
print("提升量：",np.mean(df)*0.02)

###估计最小样本量
# effect_size=|μA-μB|σ，|μA-μB|是原始均值和希望提升到的均值之差，也就是提升的绝对值，σ是标准差，取一段时间内的样本的标准差。
# alpha,默认取0.05；power（1-β），默认取0.8；ratio,
## tt_ind_solve_power(effect_size=(|μA-μB|)/σ, alpha=0.05, power=0.8, ratio=1.0, alternative="two-sided")
tt_ind_solve_power(effect_size=(0.158883)/1.217752, alpha=0.05, power=0.8, ratio=1.0, alternative="two-sided")

##实验结果检验，实验上线后达到了观察周期后的数据，data1为新版本数据，data2为老版本数据。
data_af = pd.DataFrame(
    {
    'data1':[5.679312,5.596886,6.044847,5.994368,7.532478,5.922314,4.296232,4.188054,3.777318,8.253483,7.114997,6.82596,7.213144,4.213463],
    'data2':[6.150766,4.026921,8.072727,8.764057,6.079969,5.504954,7.113292,6.33763,4.940921,6.367048,7.244069,6.365149,7.964037,3.840968]
    }
    )
    
##T检验，定义检验函数：
from scipy.stats import ttest_ind,norm,f
import numpy as np
import pandas as pd
def ftest(s1,s2):
    #'''F检验样本总体方差是否相等'''
    print("Null Hypothesis:var(s1)=var(s2)，α=0.05")
    F = np.var(s1)/np.var(s2)
    v1 = len(s1) - 1
    v2 = len(s2) - 1
    p_val = 1 - 2*abs(0.5-f.cdf(F,v1,v2))
    print(p_val)
    if p_val < 0.05:
        print("Reject the Null Hypothesis.")
        equal_var=False
    else:
        print("Accept the Null Hypothesis.")
        equal_var=True
    return equal_var

def ttest_ind_fun(s1,s2):
    #'''t检验独立样本所代表的两个总体均值是否存在差异'''
    equal_var = ftest(s1,s2)
    print("Null Hypothesis:mean(s1)=mean(s2)，α=0.05")
    ttest,pval = ttest_ind(s1,s2,equal_var=equal_var) #如果equal_var为True（默认），则执行一个标准的独立2样本检验，该检验假设总体方差相等[1]。如果为False，则执行Welch的t检验，该检验不假定总体方差相等
    if pval < 0.05:
        print("Reject the Null Hypothesis.")
    else:
        print("Accept the Null Hypothesis.")
    return pval
    
##代入实验数据进行结果检验，输出P值及检验结果
ttest_ind_fun(data_af['data1'],data_af['data2'])

检验：https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html#scipy.stats.ttest_ind
最小样本量估计：https://devdocs.io/statsmodels/generated/statsmodels.stats.power.tt_ind_solve_power

2、比率类的检验

##比率的AB测试
##导包
import pandas as pd
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
from statsmodels.stats.power import tt_ind_solve_power
from statsmodels.stats.proportion import proportion_effectsize as es 
from scipy.stats import ttest_ind,norm,f
import statsmodels.stats.weightstats as sw

##构造监测数据
data = {
    "ratio":[0.211249,0.217914,0.22124,0.20922,0.214652,0.207703,0.187119,0.204098,0.20032,0.203912,0.211707,0.205356,0.222301,0.206412,0.214494]
}
df =pd.DataFrame(data) 

##监测数据统计指标情况
print("平均转化率：",df['ratio'].mean())
print("转化率提升5%：",df['ratio'].mean()*0.05)
print("转化率提升5%后：",df['ratio'].mean()*1.05)

##估计最小样本量
tt_ind_solve_power(effect_size=es(prop1=0.2091798, prop2=0.21963879), alpha=0.05, power=0.8, ratio=1.0, alternative="two-sided")

##实验结果检验，实验上线后达到了观察周期后的数据，ratio_new为新版本数据，ratio_old为老版本数据。
data_df={
    'ratio_new':[0.20324,0.19301,0.21427,0.20777,0.20836,0.20266,0.207759,0.200588,0.198808,0.189438,0.207227,0.20823,0.207167],
    'ratio_old':[0.198468,0.212332,0.211364,0.219309,0.207997,0.201348,0.21549,0.209222,0.187228,0.198169,0.217129,0.211271,0.21982]
}
df_af = pd.DataFrame(data_df)

##两份数据可视化展示
plt.plot(df_af['ratio_new'],marker = 'o',label = 'new')
plt.plot(df_af['ratio_old'],marker = '*',label = 'old')
plt.legend()

##结果检验，P值为0.155，大于0.05，无法拒绝原假设，认为两版本的实验结果无显著差异
z_value, p_value = sw.ztest(df_af['ratio_new'],df_af['ratio_old'],alternative='two-sided')
print('统计量：',z_value)
print('P值：',p_value)

参考文档：https://devdocs.io/statsmodels/generated/statsmodels.stats.weightstats.ttest_ind