申请者评分模型(A卡)开发(基于逻辑回归)
申请者评分模型(A卡)开发(基于逻辑回归)
1项目背景
申请者评分模型应用在信贷场景中的贷款申请环节,主要是以申请者的历史信息为基础,预测未来放款后逾期或者违约的概率,为银行客户关系管理提供数据依据,从而有效的控制违约风险。
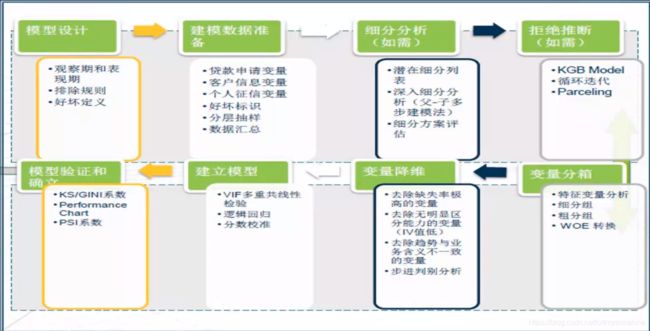
2开发流程
本次建模基本流程:
1.数据准备:收集并整合在库客户的数据,定义目标变量,排除特定样本。
2.探索性数据分析:评估每个变量的值分布情况,处理异常值和缺失值。
3.数据预处理:变量筛选,变量分箱,WOE转换、分割训练集测试集。
4.模型开发:逻辑回归拟合模型。
5.模型评估:常见几种评估方法,ROC、KS等。
6.生成评分卡
3数据准备
3.1样本选取
首先根据准入规则(如年龄、在网时长等)、行内黑名单过滤客户,再通过反欺诈模型过滤客户,得到用于建立信用评分卡的样本。
3.2数据说明
本次建模数据一共用到三个表:
“CreditFirstUse”:客户首次使用信用卡时间信息表
“CreditSampleWindow”:客户历史违约信息表(基于客户编号)
“Data_Whole”:客户基本信息表
3.3定义目标变量
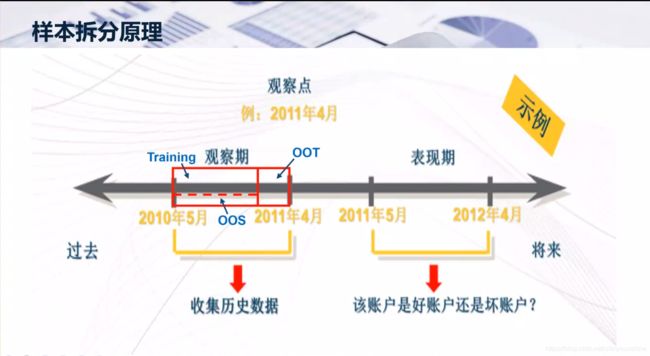
申请者评分模型需要解决的问题是未来一段时间(如12个月)客户出现违约(如至少一次90天或90天以上逾期)的概率。在这里“12个月”为“观察时间窗口”,“至少一次90天或90天以上逾期”为表现时间窗口即违约日期时长,那么我们如何确定观察时间窗口和违约日期时长(如M2算违约,还是M3算违约)呢?
3.3.1定义违约日期时长(表现时间窗口)
sample_window=pd.read_csv("CreditSampleWindow.csv")
sample_window.head()
sample_window.shape
#查看缺失值所占比例
sample_window.isnull().sum()/sample_window.shape[0]
# 选取某一个ID查看数据结构
sample_record = sample_window[sample_window.CID == sample_window.iat[4,0]]
sample_record.sort_values('START_DATE')
#去掉重复值
sample_window.drop_duplicates(inplace=True)
#去掉没有逾期阶段记录的信息
sample_window.dropna(subset=['STAGE_BEF','STAGE_AFT'],inplace=True)
sample_window.shape
#取每个 ID 每个月份的最高逾期记录也就是STAGE_AFT作为该月份的逾期指标
sample_window['START_MONTH']=sample_window.START_DATE.apply(lambda x: int(x//100)) #取年月
sample_window['CLOSE_MONTH']=sample_window.CLOSE_DATE.apply(lambda x: int(x//100))
sample_window['AFT_FLAG']=sample_window.STAGE_AFT.apply(lambda x:int(x[-1])) #取数字
sample_window.head()
#因为选取数据的时间是有一个节点的,由于系统原因,截至时间节点为0了
#所以将 CLOSE_DATE 为0的数据填补为 201806(根据缺失的业务背景确定)
sample_window.loc[sample_window.CLOSE_MONTH==0,'CLOSE_MONTH']=201806
# 提取 ID、月份、月份对应状态作为新的数据
overdue = sample_window.loc[:,["CID","START_MONTH","AFT_FLAG"]]\
.rename(columns={"START_MONTH":"CLOSE_MONTH"})\
.append(sample_window.loc[:,["CID","CLOSE_MONTH","AFT_FLAG"]],ignore_index=True)
# 生成每个订单的逾期信息,以表格形式。提取当月最差的状态
overdue = overdue.sort_values(by=["CID","CLOSE_MONTH","AFT_FLAG"])\
.drop_duplicates(subset=["CID","CLOSE_MONTH"],keep="last")\
.set_index(["CID","CLOSE_MONTH"]).unstack(1) #unstack索引的级别,level=1
overdue.columns = overdue.columns.droplevel() #删除列索引上的levels
overdue.head(2)

构建转移矩阵,横坐标(行)表示转移前状态,纵坐标(列)表示下一个月状态(转移后) , 选取连续两个月的有记录的,记录逾期阶段迁移,计算 count 录入转移矩阵。
import collections
def get_mat(df):
trans_mat=pd.DataFrame(data=0,columns=range(10),index=range(10))
counter=collections.Counter()
for i,j in zip(df.columns,df.columns[1:]):
select = (df[i].notnull()) & (df[j].notnull()) #选取连续两个月有记录的
counter += collections.Counter(tuple(x) for x in df.loc[select, [i,j]].values) #连续两个月的预期阶段转移
for key in counter.keys():
trans_mat.loc[key[0],key[1]]=counter[key] #将对应的值放进转移矩阵
trans_mat['all_count']=trans_mat.apply(sum,axis=1) #对行进行汇总
bad_count = []
for j in range(10):
bad_count.append(trans_mat.iloc[j,j+1:10].sum()) #计算转坏的数量,行表示上个月,列表示这个月
trans_mat['bad_count']=bad_count
trans_mat['to_bad']=trans_mat.bad_count/trans_mat.all_count #计算转坏的比例
return trans_mat
get_mat(overdue)

仅仅从转移矩阵来看,在逾期阶段到了 M2 时, 下一阶段继续转坏的概率达到了 67%,逾期阶段到达 M3 阶段时,下一阶段继续转坏的概率为 86%,可根据业务需要(营销、风险等等)来考虑定义进入 M2 或M3 阶段的用户为坏客户。这里由于数据的原因我们暂定为 M4。
3.3.2定义观察时间窗口
first_use=pd.read_csv("CreditFirstUse.csv",encoding="utf-8")
first_use.set_index("CID",inplace=True)
first_use["FST_USE_MONTH"]=first_use.FST_USE_DT.map(lambda x:x//100)
#计算每一笔订单第一次出现逾期 M2的月份的索引的位置
def get_first_overdue(ser):
array=np.where(ser>=2)[0]
if array.size>0:
return array[0]
else:
return np.nan
OVER_DUE_INDEX=overdue.apply(get_first_overdue,axis=1)
first_use['OVERDUE_INDEX']=OVER_DUE_INDEX
# FST_USE_MONTH在over_due的列索引中的index
first_use["START_INDEX"] =first_use.FST_USE_MONTH.map({k:v for v,k in enumerate(overdue.columns)})
first_use.loc[first_use.OVERDUE_INDEX.notnull()].head()
#查看异常数据
first_use.loc[first_use.OVERDUE_INDEX#逾期月份累计分布
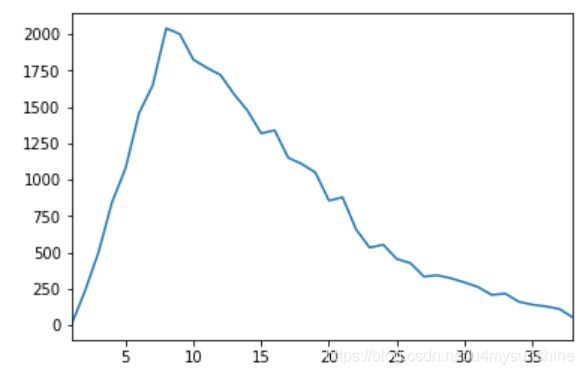
month_count.cumsum().plot()
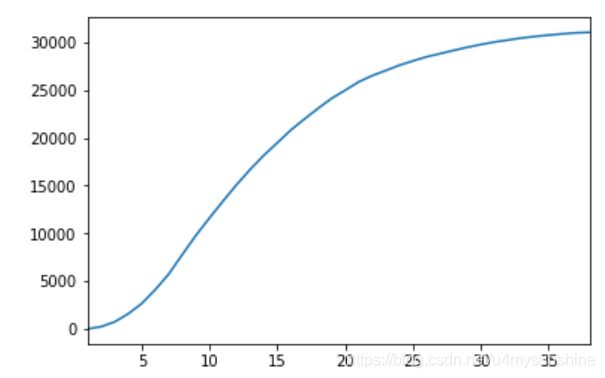
理想情况下,累计分布曲线会在某个月开始收敛。
在这里不收敛,根据业务通常定义24个月。
3.3.4好坏客户标签(y)的定义
我们定义在24个月逾期90天的客户为坏客户。
4探索性数据分析
4.1异常值
通过表查看异常值
train_data=pd.read_csv("Data_Whole.csv",index_col=0)
train_data.describe().T
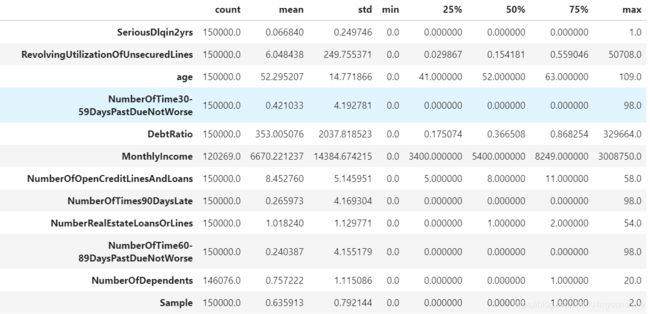
(1)分析RevolvingUtilizationOfUnsecuredLines
一般情况下为0-1.有大于1的情况:
1.主动申请提额后额度回调,一般不会大于2
2.高风险欠款后贷款额度被调的很低时,这个比例会变大
(2)分析age
age最小值为0,去看age=0的有多少
(train_data.age==0).sum()
train_data=train_data[train_data.age>0] #只有一条数据,删除
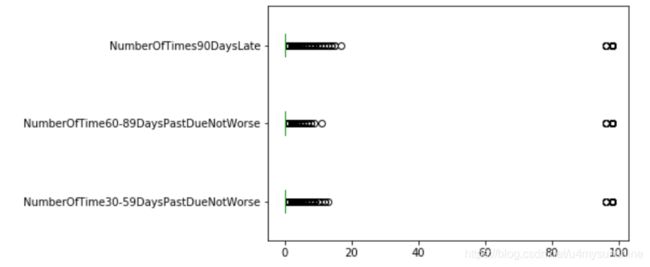
通过箱线图查看异常值
columns = ["NumberOfTime30-59DaysPastDueNotWorse",
"NumberOfTime60-89DaysPastDueNotWorse",
"NumberOfTimes90DaysLate"]
train_data[columns].plot.box(vert=False)
for col in columns:
train_data = train_data[train_data[col]<90]
4.2缺失值
缺失值大于50%或者70%的变量,不考虑这个变量。
缺失值特别小,0.1%,删除缺失值。
缺失值补全的方法:
1.单一值补全
数值型变量:样本均值或中位数
分类型变量:新增一个类别
2.分组补全(利用与其相关性较强的变量)
数值型变量:各分组均值或各分组中位数
3.模型预测
各种变量:利用多变量组合模型预测缺失值
4.WOE补全
各种变量:直接计算WOE(仅限于LR模型)
train_data.notnull().sum()/train_data.shape[0]
#查看皮尔逊相关系数
train_data.corr()
4.2.1单一值补全
def single_value_imp(df, var, fill):
# df: 输入数据名
# var: 需要补全的变量名
# fill: 填充种类 (1. mean; 2. median)
out = df.copy()
cnt = len(var)
for i in range(cnt):
x = var[i]
if fill[i] == 1:
out[x].loc[out[x].isnull()] = out[x].describe()[1]
if fill[i] == 2:
out[x].loc[out[x].isnull()] = out[x].describe()[5]
return out
temp_1 = single_value_imp(train_data, ['NumberOfDependents' , 'MonthlyIncome'], [2, 2])
temp_1.isnull().sum()
4.2.2分组补全
def grp_value_imp(df, var, col, bins, fill):
# df: 输入数据名
# var: 需要补全的变量名
# col: 分组的变量
# bins:变量分组cutoff
# fill: 填充种类 (1. mean; 2. median)
temp = df.copy()
#分箱
temp[col + '_grp'] = pd.cut(temp[col], bins)
#组内统计
if fill == 1:
grp_stat = pd.DataFrame(temp.groupby(col + '_grp')[var].mean()).rename(columns = {var: var + '_fill'})
if fill == 2:
grp_stat = pd.DataFrame(temp.groupby(col + '_grp')[var].median()).rename(columns = {var: var + '_fill'})
#分组补全
temp = pd.merge(temp, grp_stat, how = 'left', left_on = col + '_grp', right_index = True)
temp[var] = temp[var].fillna(temp[var + '_fill'])
result = temp.drop([col + '_grp', var + '_fill'], axis = 1)
return result
train_data['age'].describe().T
sub_1 = grp_value_imp(df = train_data, var = 'NumberOfDependents', col = 'age', bins = [-np.inf, 30, 40, 50, 60, 70, np.inf], fill = 2)
train_data['NumberRealEstateLoansOrLines'].describe([.90, .95, .99]).T
temp_2 = grp_value_imp(df = sub_1, var = 'MonthlyIncome', col = 'NumberRealEstateLoansOrLines', bins = [-np.inf, 0, 1, 2, 3, np.inf], fill = 2)
temp_2.isnull().sum()
4.2.3模型预测补全
import lightgbm as lgb
def fill_missing(data, to_fill, fill_type):
# data: 输入数据名
# to_fill: 需要补全的变量名
# fill_type: 填充种类 (1. 分类; 2. 回归)
df = data.copy()
columns = data.columns.values.tolist()
columns.remove(to_fill)
X = df.loc[:,columns]
y = df.loc[:,to_fill]
X_train = X.loc[df[to_fill].notnull()]
X_pred = X.loc[df[to_fill].isnull()]
y_train = y.loc[df[to_fill].notnull()]
if fill_type == 1:
model = lgb.LGBMClassifier()
else:
model = lgb.LGBMRegressor()
model.fit(X_train,y_train)
pred = model.predict(X_pred).round()
df.loc[df[to_fill].isnull(), to_fill] = pred
return df
4.2.4三种补全方法的比较
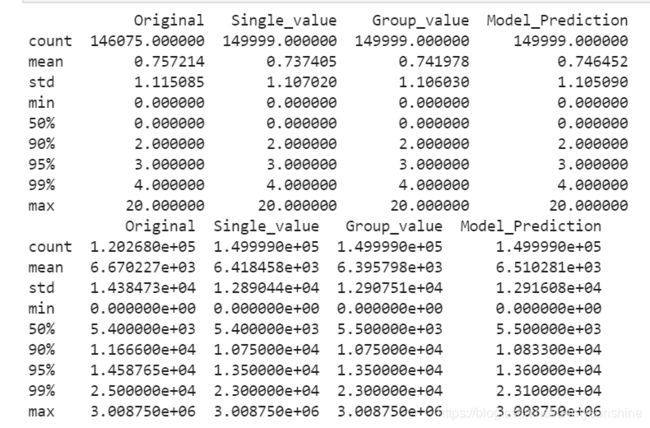
print(pd.DataFrame({'Original': train_data['NumberOfDependents'].describe([.9, .95, .99]),
'Single_value': temp_1['NumberOfDependents'].describe([.9, .95, .99]),
'Group_value': temp_2['NumberOfDependents'].describe([.9, .95, .99]),
'Model_Prediction': temp_3['NumberOfDependents'].describe([.9, .95, .99])}))
print(pd.DataFrame({'Original': train_data['MonthlyIncome'].describe([.9, .95, .99]),
'Single_value': temp_1['MonthlyIncome'].describe([.9, .95, .99]),
'Group_value': temp_2['MonthlyIncome'].describe([.9, .95, .99]),
'Model_Prediction': temp_3['MonthlyIncome'].describe([.9, .95, .99])}))
5数据预处理
5.1数据集划分
OOT = temp_3[temp_3.Sample == 2].drop(['Sample'], axis = 1)
DEV = temp_3[temp_3.Sample == 0].drop(['Sample'], axis = 1)
OOS = temp_3[temp_3.Sample == 1].drop(['Sample'], axis = 1)
#导出
DEV.to_csv("C:\Work Station\CDA\Spyder\Data\dev.csv")
OOS.to_csv("C:\Work Station\CDA\Spyder\Data\oos.csv")
OOT.to_csv("C:\Work Station\CDA\Spyder\Data\oot.csv")
5.2变量筛选
5.2.1IV值筛选
dev = pd.read_csv("dev.csv", index_col = 0, engine = "python")
from auto_bin import auto_bin
## 对每一个变量进行分析,选择合适的分箱个数
model_data.columns
# 自动分箱的添加
auto_col_bins = {"RevolvingUtilizationOfUnsecuredLines": 10,
"age": 7,
"DebtRatio": 10,
"MonthlyIncome": 9}
# 用来保存每个分组的分箱数据
bins_of_col = {}
# 生成自动分箱的分箱区间和分箱后的 IV 值
for col in auto_col_bins:
# print(col)
bins_df = auto_bin(dev, col, "SeriousDlqin2yrs",
n = auto_col_bins[col],
iv=False,detail=False,q=20)
bins_list = list(sorted(set(bins_df["min"])\
.union(bins_df["max"])))
# 保证区间覆盖使用 np.inf 替换最大值 -np.inf 替换最小值
bins_list[0],bins_list[-1] = -np.inf,np.inf
bins_of_col[col] = bins_list
# 手动分箱的添加
# 不能使用自动分箱的变量
hand_bins = {
"NumberOfTime30-59DaysPastDueNotWorse": [0, 1, 2, 3],
"NumberOfOpenCreditLinesAndLoans": [0, 1, 3],
"NumberOfTimes90DaysLate": [0, 1],
"NumberRealEstateLoansOrLines": [0],
"NumberOfTime60-89DaysPastDueNotWorse": [0, 1],
"NumberOfDependents":[0, 1, 2, 3]}
# 保证区间覆盖使用 np.inf 替换最大值 以及 -np.inf
hand_bins = {k:[-np.inf,*v, np.inf] for k,v in hand_bins.items()}
# 合并手动分箱数据
bins_of_col.update(hand_bins)
# 计算分箱数据的 IV 值
def get_iv(df,col,y,bins):
df = df[[col,y]].copy()
df["cut"] = pd.cut(df[col],bins)
bins_df = df.groupby("cut")[y].value_counts().unstack()
bins_df["br"] = bins_df[1] / (bins_df[0] + bins_df[1])
bins_df["woe"] = np.log((bins_df[0] / bins_df[0].sum()) /
(bins_df[1] / bins_df[1].sum()))
iv = np.sum((bins_df[0] / bins_df[0].sum() -
bins_df[1] / bins_df[1].sum())*bins_df.woe)
return iv ,bins_df
# 保存 IV 值信息
info_values = {}
# 保存 woe 信息
woe_values = {}
for col in bins_of_col:
iv_woe = get_iv(dev,col,
"SeriousDlqin2yrs",
bins_of_col[col])
info_values[col], woe_values[col] = iv_woe
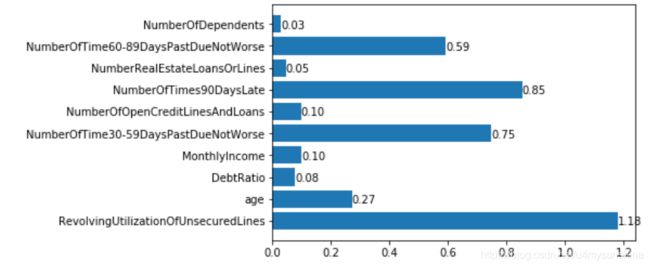
#画IV值直方图
def plt_iv(info_values):
keys,values = zip(*info_values.items())
nums = range(len(keys))
plt.barh(nums,values)
plt.yticks(nums,keys)
for i, v in enumerate(values):
plt.text(v, i-.2, f"{v:.3f}")
plt_iv(info_values)
删除iv值小于0.03的变量,这里不需要删除。
# DebtRatio为U型
#分析DebtRatio分布
sc.Eq_Bin_Plot(train_data = dev, test_data = dev, col = "DebtRatio", target = 'SeriousDlqin2yrs' , k = 10, special = 9999)
# For DebtRatio <= 1
sc.Eq_Bin_Plot(train_data = dev[dev.DebtRatio <= 1], test_data = dev[dev.DebtRatio <= 1], col = "DebtRatio", target = 'SeriousDlqin2yrs' , k = 5, special = 9999) #单调上升
# For DebtRatio > 1
sc.Eq_Bin_Plot(train_data = dev[dev.DebtRatio > 1], test_data = dev[dev.DebtRatio > 1], col = "DebtRatio", target = 'SeriousDlqin2yrs' , k = 5, special = 9999) #单调下降
# Sample Bias caused problem - DebtRatio资产负债越大风险越小?
# 资产负债高的已经在前面拒绝掉了,只能剔除此变量
#分箱并WOE赋值
dev_woe = dev.copy()
for col in bins_of_col:
dev_woe[col + '_woe'] = pd.cut(dev[col], bins_of_col[col])\
.map(woe_values[col]["woe"])
oos = pd.read_csv('oos.csv', encoding="utf8", index_col = 0, engine = "python")
oos_woe = oos.copy()
for col in bins_of_col:
oos_woe[col + '_woe'] = pd.cut(oos[col], bins_of_col[col])\
.map(woe_values[col]["woe"])
oot = pd.read_csv('oot.csv', encoding="utf8", index_col = 0, engine = "python")
oot_woe = oot.copy()
for col in bins_of_col:
oot_woe[col + '_woe'] = pd.cut(oot[col], bins_of_col[col])\
.map(woe_values[col]["woe"])
dev_woe.to_csv("dev_woe.csv")
oos_woe.to_csv("oos_woe.csv")
oot_woe.to_csv("oot_woe.csv")
5.2.2PSI筛选
dev_woe = pd.read_csv("dev_woe.csv", index_col = 0)
oos_woe = pd.read_csv("oos_woe.csv", index_col = 0)
oot_woe = pd.read_csv("oot_woe.csv", index_col = 0)
def PSI_Cal(df1,df2,var,grp):
A=pd.DataFrame(df1.groupby(by=grp)[var].count()).rename(columns={var:var+'_1'})
B=pd.DataFrame(df2.groupby(by=grp)[var].count()).rename(columns={var:var+'_2'})
C=pd.merge(A,B,how='left',left_index=True,right_index=True)
PSI_df=C/C.sum()
PSI_df['log']=np.log(PSI_df[var+'_1'])/PSI_df[var+'_2']
PSI_df['PSI']=(PSI_df[var+'_1']-PSI_df[var+'_2'])*PSI_df['log']
return PSI_df['PSI'].sum()
#变量名单
v_list = dev.drop(['SeriousDlqin2yrs'], axis = 1).columns
#计算PSI
psi_list = []
for col in v_list:
psi = PSI_Cal(dev_woe, oos_woe, col, col + '_woe')
psi_list.append(psi)
psi_df = pd.DataFrame(psi_list).rename(columns = {0: 'PSI'})
psi_df.index = v_list
psi_df
6logistic模型的建立
6.1建立线性回归模型
import statsmodels.api as sm
# 只保留WOE数据
ll = []
for col in dev_woe.columns:
if col.endswith("_woe"):
ll.append(col)
data = dev_woe.loc[:,ll]
data["SeriousDlqin2yrs"] = dev_woe["SeriousDlqin2yrs"]
# Pearson Correlation
x_corr = data.drop('SeriousDlqin2yrs', axis = 1).corr()
import statsmodels.api as sm
Y = data['SeriousDlqin2yrs']
x_exclude = ["SeriousDlqin2yrs"]
x=data.drop(x_exclude,axis=1)
X=sm.add_constant(x) #添加一个截距的列到现存的矩阵
result=sm.Logit(Y,X).fit()
result.summary()
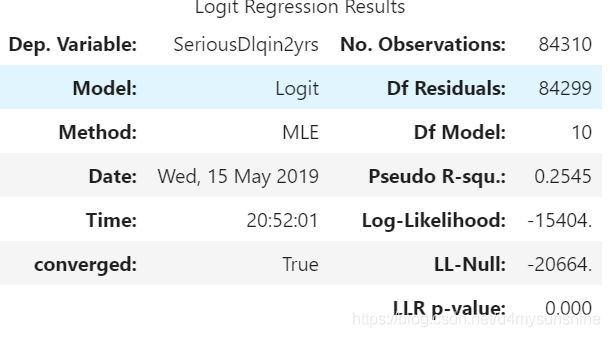
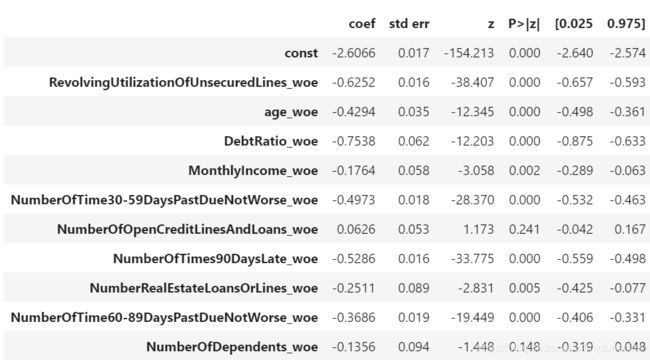
从上表可以看出,NumberOfOpenCreditLinesAndLoans_woe系数是正数,是多重共线性导致的,删除该变量。
x_exclude = ["SeriousDlqin2yrs","NumberOfOpenCreditLinesAndLoans_woe"]
x=data.drop(x_exclude,axis=1)
X=sm.add_constant(x) #添加一个截距的列到现存的矩阵
result=sm.Logit(Y,X).fit()
result.summary()
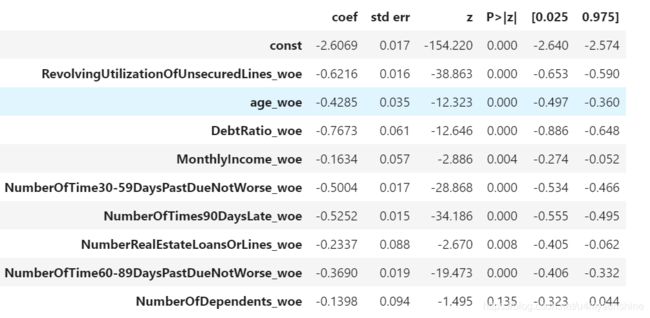
NumberOfDependents_woe>0.05,要不要删除呢?
不需要。因为0.05本身只是约定俗成的,不是大于0.05就一定重要,模型重不重要是由人来确定的;对于预测型模型重点关注预测的结果、是否过拟合等问题,对变量本身的重要性不是很关心。
6.2检查多重共线性,VIF
from statsmodels.stats.outliers_influence import variance_inflation_factor
vif = {}
for i in range(x.shape[1]):
vif[x.columns[i]] = variance_inflation_factor(np.array(x), i)
vif
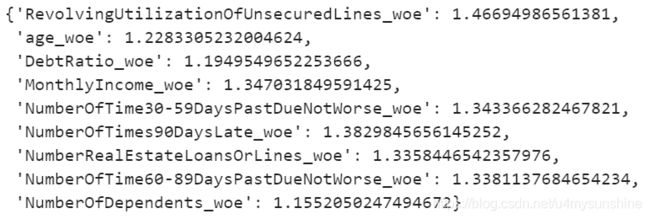
VIF都很小,其实VIF在这里检查不出来多重共线性。很多传统的方法,用到大数据上会失效。
在回归中,为什么不能有多重共线性?
因为在回归中,有个很大的假设,回归中的某个自变量X1系数w1表示挡其他自变量不变时,x1每增加1,因变量增加w1
但是在实际中,多重共线性很普遍
在树的模型中就不用考虑多重共线性
7模型评估
7.1ROC曲线&KS
def app_pred(df, x_list,y_col,result):
'''
:param df: 包含目标变量的数据集,dataframe
:param x_list: 所有自变量的列名
:param y_col: 目标变量,str
:param result:返回包含预测值'prob'的df
:return: KS值
'''
df=df.copy()
ll = []
for col in df.columns:
if col.endswith("_woe"):
ll.append(col)
data = df.loc[:,ll]
data[y_col] = df[y_col]
x=data.drop([y_col],axis=1)
x1=sm.add_constant(x)
result=result.predict(x1)
df['prob']=result
return df
def KS(df, score, target):
'''
:param df: 包含目标变量与预测值的数据集,dataframe
:param score: 得分或者概率,str
:param target: 目标变量,str
:return: KS值
'''
total = df.groupby([score])[target].count()
bad = df.groupby([score])[target].sum()
all = pd.DataFrame({'total':total, 'bad':bad})
all['good'] = all['total'] - all['bad']
all[score] = all.index
all.index = range(len(all))
all = all.sort_values(by=score,ascending=False)
all['badCumRate'] = all['bad'].cumsum() / all['bad'].sum()
all['goodCumRate'] = all['good'].cumsum() / all['good'].sum()
KS = all.apply(lambda x: x.badCumRate - x.goodCumRate, axis=1)
return max(KS)
import scikitplot as skplt
def ROC_plt(df, score, target):
'''
:param df: 包含目标变量与预测值的数据集,dataframe
:param score: 得分或者概率,str
:param target: 目标变量,str
'''
proba_df=pd.DataFrame(df[score])
proba_df.columns=[1]
proba_df.insert(0,0,1-proba_df)
skplt.metrics.plot_roc(df[target], #y真实值
proba_df, #y预测值
plot_micro=False, #绘制微平均ROC曲线
plot_macro=False); ##绘制宏观平均ROC曲线
#训练集预测
dev_woe.drop(["NumberOfOpenCreditLinesAndLoans_woe",'NumberOfOpenCreditLinesAndLoans'],axis=1,inplace=True)
dev_pred = app_pred(dev_woe, x_list,"SeriousDlqin2yrs",result)
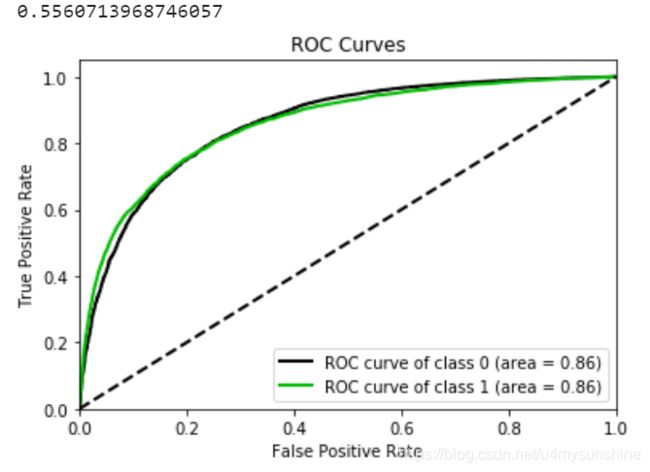
#计算KS(Compare TPR and FPR - 不同阈值下检测出坏样本比例和检测错的好样本比例)
#We'd like TRP to be large and FRP otherwise
print(KS(dev_pred, "prob", "SeriousDlqin2yrs"))
#画ROC图,并计算AUC
ROC_plt(dev_pred, "prob", "SeriousDlqin2yrs")
#测试集预测
oos_woe.drop(["NumberOfOpenCreditLinesAndLoans_woe",'NumberOfOpenCreditLinesAndLoans'],axis=1,inplace=True)
oos_pred = app_pred(oos_woe, x_list, "SeriousDlqin2yrs", result)
# 计算OOS的KS
print(KS(oos_pred, "prob", "SeriousDlqin2yrs"))
# 预测结果为对应 1 的概率,转换为数组用于绘图
ROC_plt(oos_pred, "prob", "SeriousDlqin2yrs")

从同时间的测试集无法看出模型是否过拟合,还要看跨时间的测试集。
#跨时间测试集
oot_woe.drop(["NumberOfOpenCreditLinesAndLoans_woe",'NumberOfOpenCreditLinesAndLoans'],axis=1,inplace=True)
oot_pred = app_pred(oot_woe, x_list, "SeriousDlqin2yrs", result)
# 计算OOT的KS
print(KS(oot_pred, "prob", "SeriousDlqin2yrs"))
# 预测结果为对应 1 的概率,转换为数组用于绘图
ROC_plt(oot_pred, "prob", "SeriousDlqin2yrs")

在现实中,跨时间测试集的Gini系数下降在10%以内,都是正常的。
8阈值选择
from sklearn.metrics import confusion_matrix,accuracy_score,precision_score,recall_score,f1_score
#根据通过率选阈值
def ar_select(df,prob,ar):
loc=int(df.shape[0]*ar)
ordered=df.sort_values([prob]).reset_index()
return ordered.loc[loc,prob]
#根据坏账率选阈值
def br_select(df,target,prob,br,ar=0.3,close=0.001):
cutoff_list=sorted(list(set(df[prob])))
ar_cutoff=ar_select(df,prob,ar)
loc=cutoff_list.index(ar_cutoff)
for i in range(loc,len(cutoff_list)):
cutoff=cutoff_list[i]
p=np.where(df[prob]>=cutoff,1,0)
cm=confusion_matrix(df[target],p)
bad_rate=cm[1][0]/(cm[0][0]+cm[1][0])
if abs(bad_rate-br) cut_off1, 1, 0)
cm(dev_pred, "SeriousDlqin2yrs", p_dev)
#根据坏账率选择阈值
cut_off2 = br_select(dev_pred, "SeriousDlqin2yrs", 'prob', br = 0.03, close = 0.005) #0.03的坏账率
cut_off2
p_dev2 = np.where(dev_pred['prob'] > cut_off2, 1, 0)
cm(dev_pred, "SeriousDlqin2yrs", p_dev2)
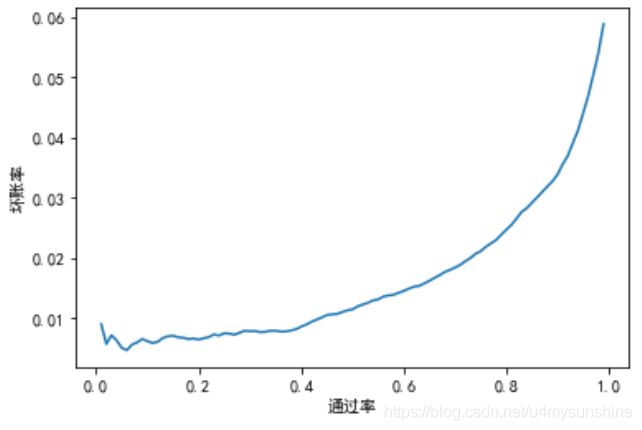
#画通过率和坏账率的图
def plt_a_b(df,target,prob):
app_rate=np.linspace(0,0.99,100)
cut_off_list=[]
bad_rate=[]
for i in range(len(app_rate)):
loc=int(df.shape[0]*app_rate[i])
ordered=df.sort_values([prob]).reset_index()
sub_cut_off=ordered.loc[loc,prob]
cut_off_list.append(sub_cut_off)
pre=np.where(df[prob]>=sub_cut_off,1,0)
cm=confusion_matrix(df[target],pre)
sub_bad_rate=cm[1][0]/(cm[0][0]+cm[1][0])
bad_rate.append(sub_bad_rate)
data={'cut_off':cut_off_list,'app_rate':app_rate,'bad_rate':bad_rate}
ab_table=pd.DataFrame(data)
#设置rc动态参数
plt.rcParams['font.sans-serif']=['Simhei'] #显示中文
plt.rcParams['axes.unicode_minus']=False #显示负号
plt.plot(app_rate,bad_rate)
plt.xlabel("通过率")
plt.ylabel("坏账率")
return ab_table
cut_off_tab = plt_a_b(dev_pred, "SeriousDlqin2yrs", 'prob')
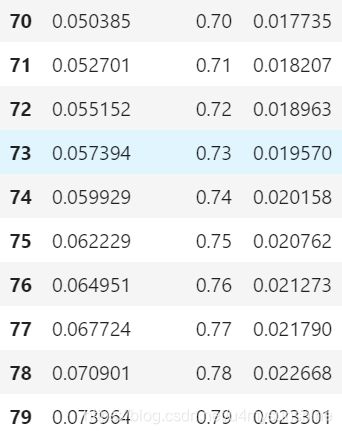
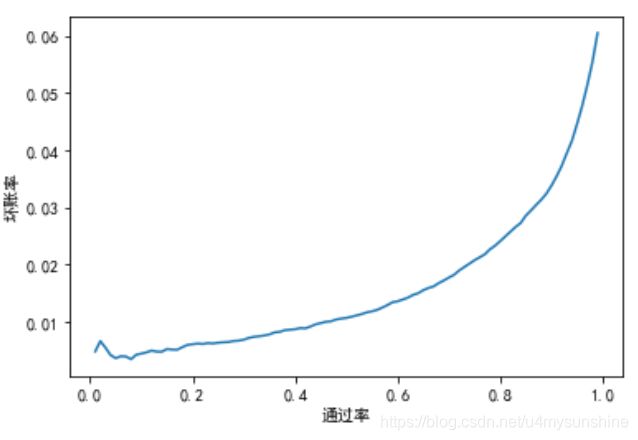
根据业务部门期望的通过率或者是能够忍受的坏账率来选择对应的cut_off
在这里选择通过率为73%,坏账率接近2%的cut_off2 = 0.057394
注意:为了与业务相联系,通常坏账率转换为金额。
#计算测试集
def apply_cutoff(df,target,prob,cut_off):
df=df.copy()
pre=np.where(df[prob]>=cut_off,1,0)
df['pre']=pre
return df
cut_off2 = 0.057394
apply_cutoff(dev_pred, "SeriousDlqin2yrs", 'prob', cut_off2)
apply_cutoff(oos_pred, "SeriousDlqin2yrs", 'prob', cut_off2)
apply_cutoff(oot_pred, "SeriousDlqin2yrs", 'prob', cut_off2)
#测试集画通过率和坏账率的图
LR_ab_tab = plt_a_b(oos_pred, "SeriousDlqin2yrs", 'prob')
LR_ab_tab.to_csv("ab_tab_LR.csv")
9信用评分
- score=A-B*log(odds)
- 求解A,B需要两个假设:
- 1.特定违约概率下的预期分值
- 2.指定违约概率翻倍的分数PDO
base_odds=1/40
base_score=700
PDO=40
B=PDO/np.log(2)
A=base_score+B*np.log(base_odds)
del woe_values['NumberOfOpenCreditLinesAndLoans']
b_score = A - B*result.params["const"]
para=result.params[1:]
para.index=para.index.map(lambda x:x[:-4])
file = "ScoreData1.csv"
with open(file,"w") as fdata:
fdata.write(f"base_score,{base_score}\n")
for col in para.index:
score = woe_values[col]["woe"] * (-B*para[col])
score.name = "Score"
score.index.name = col
score.to_csv(file,header=True,mode="a")