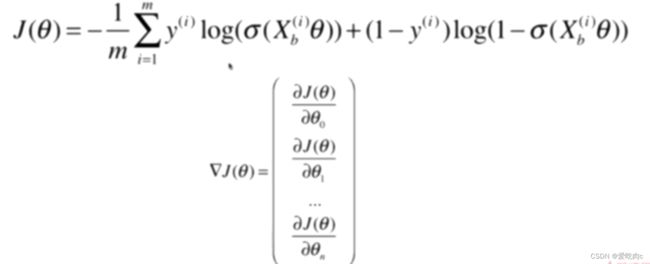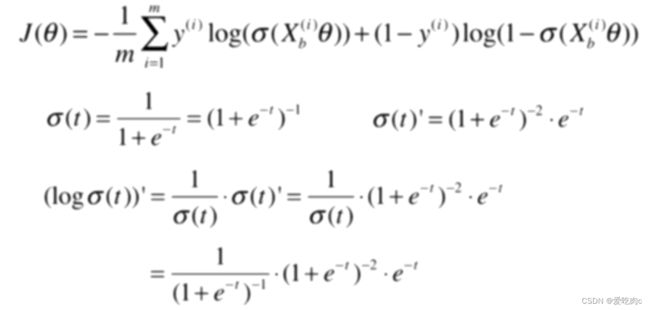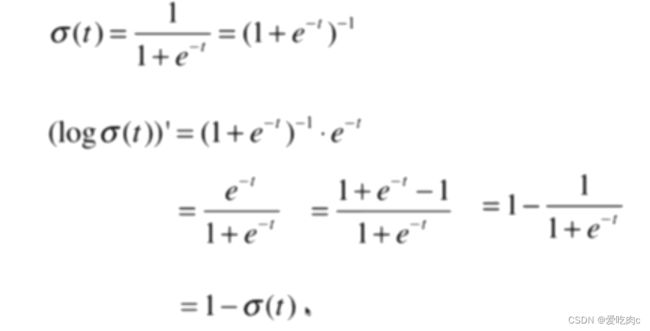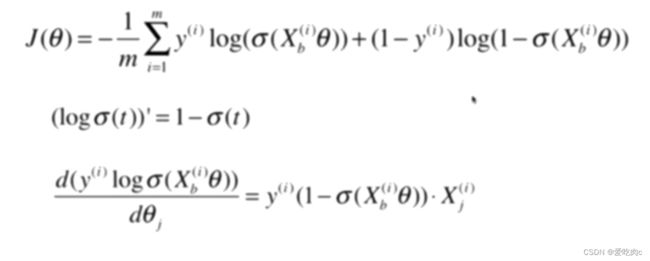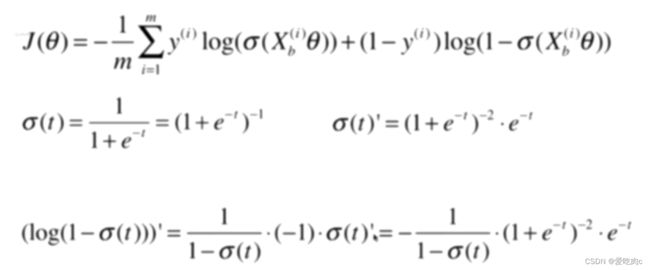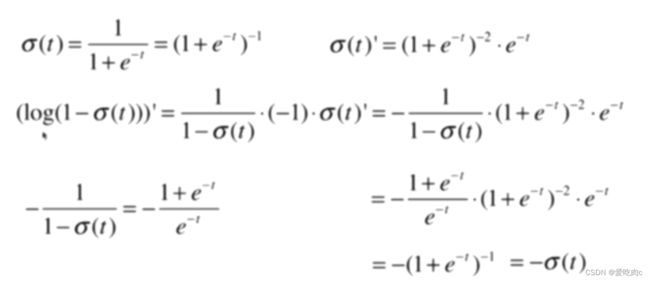逻辑回归Logistic Regression

---

一、逻辑回归

1、基本概述

逻辑回归是用来解决分类问题的。

如图，逻辑回归是将样本特征与概率结合起来，得到的是一个数（概率），从这点来说，逻辑回归是一个回归问题。但是得到概率之后，通过概率来将样本分类，从这点来看，逻辑回归是一个分类问题。但是逻辑回归只能解决二分类问题。

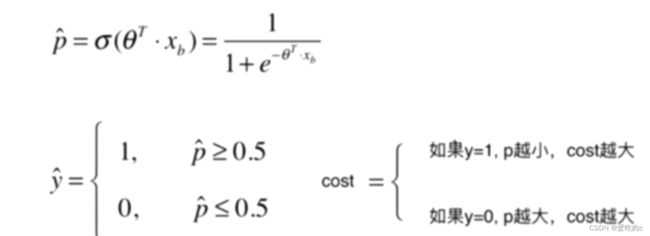
我们通过逻辑回归得到的数值是一个概率，我们知道，概率是从0-1的，但是如果我们只是通过theta*X得到的范围是负无穷到正无穷，此时我们可以再通过一个signama函数，来将值变为0-1

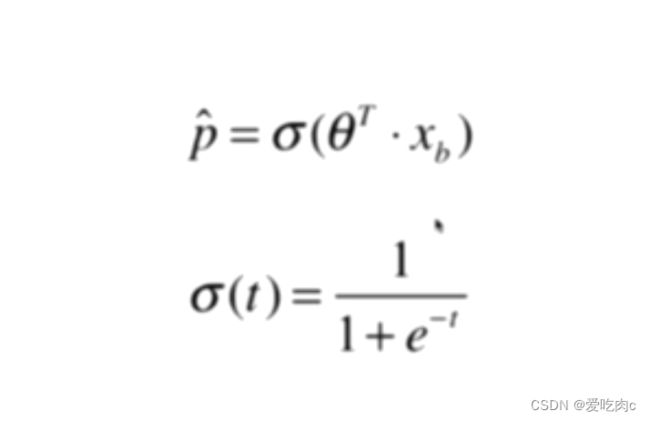
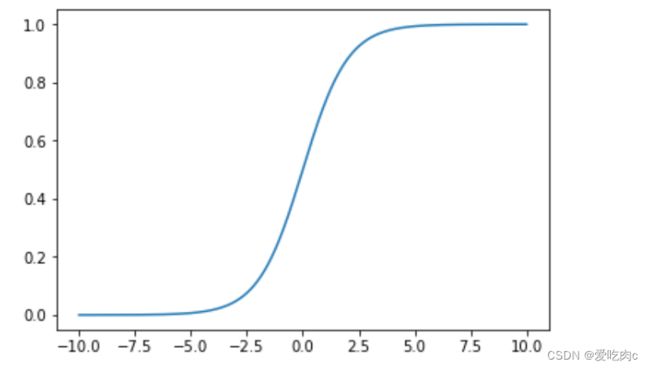
我们把这个函数叫做Sigmoid
我们可以通过代码来观察一下这个函数：

import numpy as np
import matplotlib.pyplot as plt
def sigmoid(t):
    return 1/(1+np.exp(-t))
x=np.linspace(-10,10,500)
y=sigmoid(x)
plt.plot(x,y)
plt.show()

2、问题

如果是线性回归问题，我们可以通过损失函数y-y预测 来求最佳的theta，但是对于逻辑回归我们如何让来求theta来最大程度的获取x对应的分类y呢?

二、逻辑回归的损失函数

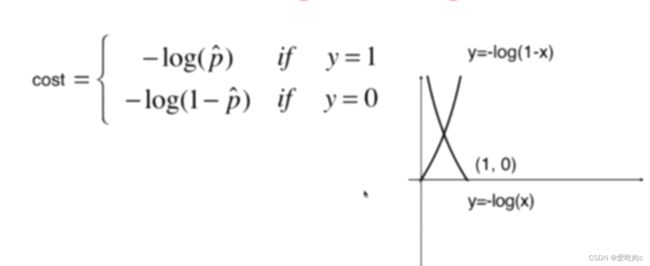
因为概率p是0-1之间，所以只取0-1之间即可。推导过程看图我觉得还挺简单的。

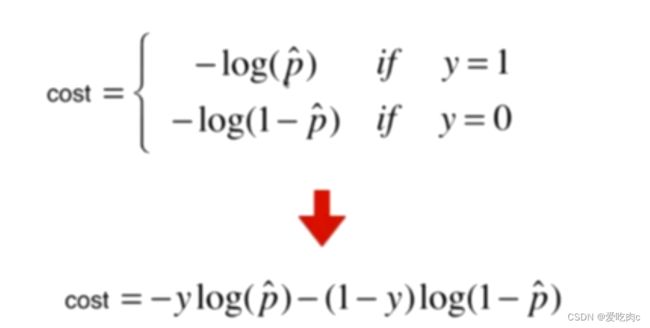
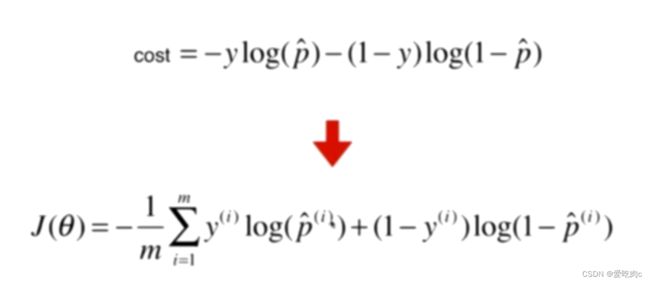
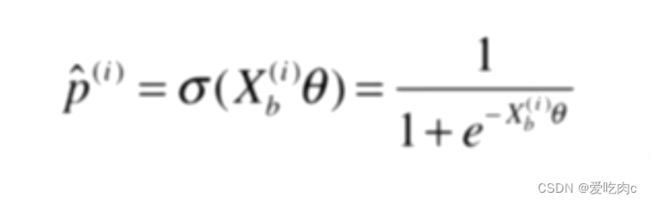
求逻辑回归的theta没有公式解，不像线性回归有正规方程解，但是它可以通过梯度下降法求出。

三、梯度下降法的具体推导过程（可忽略只记住公式即可）

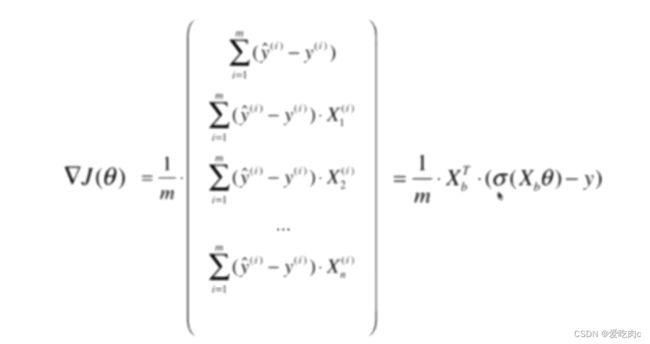
1.推导

		其实和线性回归之后进行向量化有很大的相同之处，但是如果搞不懂也没关系。只需记住公式即可。

2.代码实现逻辑回归算法

# 时间：2022/11/16 10:32
# cky
import numpy as np
from sklearn.metrics import accuracy_score
class LogicRegression:
    def __init__(self):
        self._theta=None
        self.interception_=None
        self.coef_=None
    def _sigmoid(self,t):
        return 1./(1.+np.exp(-t))
    def fit(self,X_train,y,eta=0.01,n_iters=1e3):
        assert X_train.shape[0]==y.shape[0],\
        "the size of X_train must be equal the size of y_train"
        #损失函数
        def J(X_b, y, theta):
            y_hat = self._sigmoid(X_b.dot(theta))
            try:
                return -np.sum(y*np.log(y_hat)+(1-y)*np.log(1-y_hat))/len(y)
            except:
                return float('inf')  # 防止eta不合理出错

        # 求梯度
        def dJ(X_b, y, theta):
            return X_b.T.dot(self._sigmoid(X_b.dot(theta))-y)/len(X_b)

    # 梯度下降过程
        def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e3, epsilon=1e-8):
            theta = initial_theta
            i_iters = 0
            while i_iters < n_iters:
                last_theta = theta  # 保存上次theta
                gradient = dJ(X_b, y, theta)
                theta = theta - eta * gradient
                if (np.abs(J(X_b, y, theta) - J(X_b, y, last_theta)) < epsilon):
                    break
                i_iters += 1
            return theta
        x_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        initial_theta=np.zeros(x_b.shape[1])
        self._theta = gradient_descent(x_b,y, initial_theta, eta, n_iters=1e3)
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self
    #获得概率向量
    def predict_proba(self,X_predict):
        x_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])

        return self._sigmoid(x_b.dot(self._theta))
    #获得预测结果 0或1
    def predict(self,X_predict):
        proba=self.predict_proba(X_predict)
        return np.array(proba>=0.5,dtype=int)
    def score(self,X_test,y_test):
        y_predict=self.predict(X_test)
        return accuracy_score(y_test,y_predict)
        #分类准确度

调用
这里使用鸢尾花数据

from sklearn import datasets
iris=datasets.load_iris()
x=iris.data
y=iris.target
x=x[y<2,:2]  #选取前两个特征，是为了之后方便可视化
y=y[y<2]  #因为逻辑回归只能解决二分类问题，所以这里采用0，1
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,random_state=666)  #如果你们也使用的是随机种子666 的 话 则我们的结果应该是相同的
Logicreg=LogicRegression()
Logicreg.fit(x_train,y_train)
print(Logicreg.score(x_test,y_test))
print(Logicreg.predict_proba(x_test))
print(Logicreg.predict(x_test))

结果：
1.0
[0.7112758 0.80710316 0.39188175 0.23930882 0.28760785 0.24500555
0.30715316 0.86623755 0.78703143 0.60676817 0.30058671 0.16041586
0.44491703 0.28760785 0.65046943 0.62880559 0.64327824 0.46812788
0.32746459 0.42194405 0.2567548 0.40687863 0.78703143 0.81671681
0.34123216]
[1 1 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0]

	这里分类准确度是1，代表全部分类成功，是因为我们的数据比较简单。