数值微分计算方法——《数值计算方法》

《数值计算方法》系列总目录

第一章 误差序列实验
第二章 非线性方程f(x)=0求根的数值方法
第三章 CAD模型旋转和AX=B的数值方法
第四章 插值与多项式逼近的数值计算方法
第五章 曲线拟合的数值方法
第六章 数值微分计算方法
第七章 数值积分计算方法
第八章 数值优化方法

---

---

一、算法原理

1、中心差分和理查森外推法原理

  数值导数的公式对开发求解常微分方程和偏微分方程边值问题的算法很重要。数值微分的例子通常采用已知的函数,这样数值近似值可以与精确解进行比较。本章主要介绍研究数值微分精确性的相关理论。首先我们给出导数的定义以及差商的概念。
函数$f(x)$的导数可以表示为：
$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$  从公式中我们可以提取出差商的定义式：
$$D_k=\frac{f(x+h_k)-f(x)}{h_k},k=1,2,...,n,...$$  因此 ，我们可以选择一个序列$\{{\mathrm{h}}_k\}$，其中$h_k\to 0$，因此我们可以计算序列的极限，并用得到的解作为函数的导数的近似值。那么，如何选取序列才能够得到理想的结果呢？在一个区间内，当序列选取的点过于疏松时则会导致误差过大，其得到的结果就是两点之间的斜率值，与步长趋于0时得到的导数值差别过大；而当序列选取的点过于密集时，由于计算机的截断误差会导致$f(x+h)$和$f(x)$差别较小，从而使得其差值为0. 例如,设有函数$f(x)=e^x$,并使用步长$h=1,1/2$和$1/4$分别构造位于$(0,1)$和$(h,f(h))$之间点的割线。当$h$足够小,割线接近于对应的切线 ,但要用$h=0.00001$才能得到可接受的答案,采用这个$h$值,图中的切线和割线将无法区分。
  因此不容易求出式中极限的数值近似解。序列在$Dk$在步长适当时最接近真实值,然后逐渐偏离$e$。在程序中,当$|D_{N+1}-D_N|\ge |D_N-D_{N-1}|$时,才不会进一步计算序列$\{D_k\}$中的项。这用来确定在项偏离极限前的最佳近似值。下面将研究根据较大的$h$值,得到合理精度的近似值的公式。
  如果函数$f(x)$在点$x$的左边和右边的值可计算,则最佳二点公式$(two-pointformula)$包含$x$两边的两个对称的横坐标。因此我们可以得到另一种计算导数近似值的方法，即中心差分公式。不同中心差分公式具有不同的精度，下面给出常用的两种中心差分公式。

1、精度为$O(h2)$的中心差分公式

$$f^{\prime }(t)\approx \frac{f(x+h)-f(x-h)}{2h}$$  其中，要求函数在区间$[a,b]$上三阶可导，且$x-h,x,x+h\in [a,b]$，并且在区间内存在数$c$有
$$\begin{gathered} f^{\prime }(t)=\frac{f(x+h)-f(x-h)}{2h}+E_{trunc}(f,h) \\ {E}_{trunc}(f,h)=-\frac{h^2{f}^{(3)}(c)}{6}=O(h^2) \end{gathered}$$  其中，$E(f,h)$项称为截断误差。精度为$O(h^2)$的中心差分公式的证明使用泰勒公式的二阶展开计算的，其中截断误差项来源于泰勒展开多项式的余项。利用在x两端的函数差分值的展开和消元可以得到精度为$O(h^2)$的中心差分公式。

2、精度为$O(h4)$的中心差分公式

$$f^{\prime }(x)\approx \frac{-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)}{12h}$$  其中，要求函数在区间$[a,b]$上五阶可导，且$x-2h,x-h,x,x+h,x+2h\in [a,b]$，并且在区间内存在数$c$有
$$\begin{gathered} f^{\prime }(x)=\frac{-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)}{12h}+E_{trunc}(f,h) \\ {E}_{trunc}(f,h)=\frac{h^4{f}^{(5)}(c)}{30}=O(h^4) \end{gathered}$$  中，$E(f,h)$项称为截断误差。精度为$O(h^4)$的中心差分公式的证明使用泰勒公式的四阶展开计算的，其中截断误差项来源于泰勒展开多项式的余项。利用在$x$两端的函数差分值的展开和消元可以得到精度为$O(h^4)$的中心差分公式。
  设$|f^{(5)}(c)|$对于$c\in [a,b]$是有界的,则式中的截断误差以与$h4$相同的方式趋近于零,表示为$O(h^4)$。现在比较公式(3)和公式(5)。设$f(x)$有5阶连续导数,而且$|f^{(3)}(c)|$和$|f^{(5)}(c)|$基本相同,则4阶公式的截断误差为$O(h^4)$，2阶公式的截断误差为$O(h^2)$，所以公式(5)的截断误差比公式(3)的截断误差更快地趋近于零。这样在公式(5)中可使用更大的步长。
  那么，关于数值微分的一个重要课题是研究计算机的舍人误差。下面将对此进行更深入的分析。设用计算机进行数值计算,而且有
$$f(x_0-h)=y_{-1}+e_{-1},f(x_0+h)=y_1+e_1$$  其中$f(x_0-h)$和$f(x_0+h)$是数值$y_{-1}$和$y_1$的近似值, $e_{-1}$和$e_1$分别是相关的舍入误差。则误差分析可通过如下方程进行解释，即
$$E(f,h)=E_{round}(f,h)+E_{trunc}(f,h)=\frac{e_1-e_{-1}}{2h}-\frac{h^2{f}^{(3)}(c)}{6}$$  因此可以推出两种精度的中心差分公式的误差表达式，即

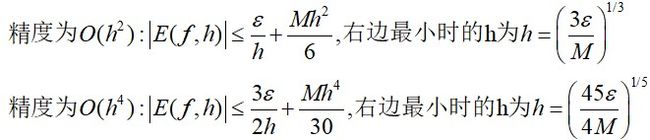
  因此在选取步长时一定要慎重选取步长来达到满足条件的精度要求。
  下面在介绍一种联系不同精度的中心差分公式的递推表达式，即理查森外推法。

2、理查森外推法

  首先，通过研究公式(3)和公式(5)的关系，可以得到由低阶公式推导高阶公式的方法，利用不同步长的一阶中心差分公式表达式，通过消元可以得到二阶中心差分公式
$$f^{\prime }(x_0)\approx \frac{4D_0(h)-D_0(2h)}{3}=\frac{-f_2+8f_1-8f_{-1}+f_{-2}}{12h}$$  这种从低阶公式中推导出求解$f^{\prime }(x_0)$高阶导数的方法称为外推法。相关的证明要求式(3)的误差项可扩展为一个包含$h$的偶次幂的序列。这里已经看到了如何使用步长$h$和$2h$消去包含$h$的项。类似的可以推出三阶中心差分公式
$$f^{\prime }(x_0)\approx \frac{16D_1(h)-D_1(2h)}{15}$$  因此可以得到理查森外推法的一般形式
设$f^{\prime }(x_0)$的两个精度为$O(h_{2}k)$的近似值分别为$D_{k-1}(h)$和$D_{k-1}(2h)$，而且满足
$$\begin{gathered} f^{\prime }(x_0)=D_{k-1}(h)+c_1{h}^{2k}+c_2{h}^{2k+2}+... \\ {f}^{\prime }(x_0)=D_{k-1}(2h)+4^k{c}_1{h}^{2k}+4^{k+1}{c}_2{h}^{2k+2}+... \end{gathered}$$  这样可以得到近似值表达式
$$f^{\prime }(x_0)=D_k(h)+O(h^{2k+2})=\frac{4D_{k-1}(h)-D_{k-1}(2h)}{4^k-1}+O(h^{2k+2})$$  这样即可得到由低阶公式中推导出求解$f^{\prime }(x_0)$高阶导数的方法。

2、牛顿、拉格朗日多项式微分原理

  在前面的小节中,求解 的公式需要函数在x的两边值可计算,所以它们称为中心差分公式。可用泰勒级数构造求解高阶导数的公式，与第一节求解的区别仅仅在于消元时的方法不一样。

  由第一节的分析可知，计算导数数值的误差主要来源于计算机的截断误差和舍入误差。其中，当步长太小时，舍入误差会变大；当步长太大时，截断误差会变大，因此会陷入一个步长两难的问题。由第一节分析可知，当采用更高阶的公式，可以使得在较大步长时也能使误差在范围之内，因此可以利用理查森外推法进行高阶公式的求解。一般来说,如果进行数值微分计算,计算结果只有计算机表示能力的一半精度。除非碰巧找到一个优化步长,否则通常会丢失多位有效数字。所以,在进行数值微分计算时要小心处理。当对精度有限的试验数据进行计算时,困难更大。如果必须根据数据集求数值导数,应该先用最小二乘法进行曲线拟合,然后对曲线函数进行微分。因此，我们可以选用拉格朗日多项式和牛顿多项式进行曲线拟合。

1、 拉格朗日多项式微分

  如果函数必须在$x$的某一边计算,则不能使用中心差分公式。位于$x$的右边(左边)的等距横坐标的公式称为前向(后向)差分公式。通过对拉格朗日插值多项式进行差分可得到这些公式。其中一个常用的公式推导如下：
$$\begin{gathered} f(t)\approx f_0\frac{(t-x_1)(t-x_2)(t-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}+f_1\frac{(t-x_0)(t-x_2)(t-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} \\ +f_2\frac{(t-x_0)(t-x_1)(t-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}+f_3\frac{(t-x_0)(t-x_1)(t-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)} \\ {f}^{\prime \prime }(t)\approx f_0\frac{2\left((t-x_1)+(t-x_2)+(t-x_3)\right)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}+f_1\frac{2\left((t-x_0)+(t-x_2)+(t-x_3)\right)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} \\ +f_2\frac{2\left((t-x_0)+(t-x_1)+(t-x_3)\right)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}+f_3\frac{2\left((t-x_0)+(t-x_1)+(t-x_2)\right)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)} \\ t=x_0,x_i-x_j=(i-j)h \\ {f}^{\prime \prime }(x_0)\approx \frac{2f_0-5f_1+4f_2-f_3}{3h^2} \end{gathered}$$  以此类推，还有其他公式可以推导出来，在这里不一一展示，一般情况下比较常用的是牛顿多项式。

2、 牛顿多项式微分

  通过第四章的插值多项式部分可以知道，牛顿多项式可以写成形如
$$P(t)=a_0+a_1(t-t_0)+a_2(t-t_0)(t-t_1)$$  因此，对其求一阶导数，可以得到
$$\begin{gathered} P^{\prime }(t)=a_1+a_2\left((t-t_0)+(t-t_1)\right) \\ {P}^{\prime }(t_0)=a_1+a_2\left(t_0-t_1\right)\approx f^{\prime }(t_0) \\ {a}_0=f(t_0) \\ {a}_1=\left(f(t_1)-f(t_0)\right)/(t_1-t_0) \\ {a}_2=\left(\frac{f(t_2)-f(t_1)}{t_2-t_1}-\frac{f(t_1)-f(t_0)}{t_1-t_0}\right)/(t_2-t_0) \end{gathered}$$  牛顿多项式的优点在于所选取的结点可以不用是等距的，因此通过改变节点的选取，从而可以推导出不同的前向与后向差分公式。
当所选取的是$t_0=x,t_1=x+h,t_2=x+2h$,可以得到
$$\begin{gathered} a_1=\left(f(x+h)-f(x)\right)/h \\ {a}_2=\left(f(x)-2f(x+h)+f(x+2h)\right)/2h^2 \end{gathered}$$  带入牛顿多项式中可以得到
$$\begin{gathered} P^{\prime }(x)=\frac{f(x+h)-f(x)}{h}+\frac{-f(x)+2f(x+h)-f(x+2h)}{2h} \\ {P}^{\prime }(x)=\frac{-3f(x)+4f(x+h)-f(x+2h)}{2h}\approx f^{\prime }(x) \end{gathered}$$  因此可以得到一阶导数的二阶前向差分公式。同样的，当选取不同的结点，同样可以得到一阶导数的二阶后向或中心差分公式。我们可以进行推导，是牛顿多项式用于求解导数近似值具有一般规律以及普适性。当我们选取$N+1$个结点时，可以构造N次牛顿多项式对函数值进行近似，即
$$\begin{gathered} P(t)=a_0+a_1(t-t_0)+a_2(t-t_0)(t-t_1)+a_3(t-t_0)(t-t_1)(t-t_2)+... \\ +a_N(t-t_0)...(t-t_{N-1})+... \end{gathered}$$  当对多项式求一阶导数，可以得到函数一阶导数的近似表达式，即

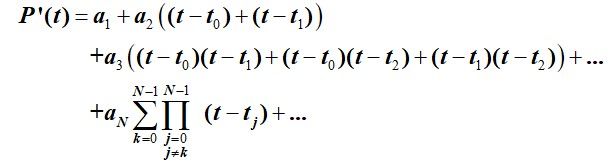
  特殊情况下，当在t0处，我们可以得到导数近似值为
$$P^{\prime }(t_0)=a_1+a_2\left(t_0-t_1\right)+a_3(t_0-t_1)(t_0-t_2)+...+a_N\prod _{j=1}^{N-1}(t_0-t_j)+...$$  通过构建牛顿多项式，我们可以很方便的得到其导数表达式，因为对于多项式来说求导是较为方便的，而牛顿多项式的拟合效果也较为理想，因此可以将其导数表达式作为导数近似值，并且可以推测，当结点选择越多，其拟合效果越好，得到的导数近似值也更精确。同时，经过实验，对于导数求解时外插值会出现明显的失真，因此应当尽量避免外插值的情况。

二、实验内容及核心算法代码

1、中心差分和理查森外推法原理实现

  由第一节原理可知，数值微分的例子通常采用已知的函数,这样数值近似值可以与精确解进行比较，序列在$D_k$在步长适当时最接近真实值，不同中心差分公式具有不同的精度，在选取步长时一定要慎重选取步长来达到满足条件的精度要求。
  因此，在利用中心差分公式进行导数近似值求解时，需要首先考虑结果的精度要求并选取合适的步长。其次，再利用理查森外推法进行求解导数近似值高阶公式时，可以构建形如求解牛顿多项式系数表一样的导数值表，并利用迭代法。一般来说，更高阶的导数近似值在步长相同时具有更高的精度。因此其流程大致为：

1. 通过步长选取的条件以及精度要求，选取适当的步长。
2. 构建第一列的导数近似值表，即一阶导数近似值。
3. 从第二行开始，每次步长减小为原来一半，并依次对每一列进行递推公式的求解，求出每一阶导数近似值。

  以下通过几个实例来验证理论的准确性。

1. 利用两种不同精度中心差分公式求解下列函数的的导数值，其中要求步长不断迭代，并在偏离真值前停止。
2. 利用理查森外推法求解第一题中函数导数的近似值。

  对于第一题，可以选取初始步长$h_0=0.5$，并设置最大迭代次数为50，容差为$1e^{-9}$，每次步长减小为之前的十倍。当相邻两次求解的导数近似值在容差范围内或满足迭代停止条件即发散判定依据或超出最大迭代次数，从而选择停止迭代。返回迭代次数判断两种精度的迭代次数。对于第二题，可以按照流程图中的步骤，重新设置容差、步长以及最大迭代次数，从而得到每一步求解的数值，最终得到导数近似值。

  其核心函数算法代码为：

第一题：
double CmpDkDiffquotientbyerrH4(double (*fun)(double), const double x, const double hk)
{
	double f_2, f_1, f1, f2, dk;
	f_2 = fun(x - 2 * hk);
	f_1 = fun(x - hk);
	f2 = fun(x + 2 * hk);
	f1 = fun(x + hk);
	dk = (-f2 + 8 * f1 - 8 * f_1 + f_2) / (12 * hk);
	return dk;
}
//
double CmpDkDiffquotientbyerrH2(double (*fun)(double), const double x, const double hk)
{
	double dk;
	dk = fun(x + hk) - fun(x);
	return dk / hk;
}
void CmpDkbyIterwithinErr(double (*fun)(double), double** valset, double x0, const double hk, int& iter, double eps, const int N)
{
	iter = 1;
	double hk_t, xk, fk, fk1, Dfk, err;
	valset[0][0] = iter;
	valset[0][1] = hk;
	valset[0][2] = CmpDkDiffquotientbyerrH2(fun, x0, hk);
	valset[0][3] = NULL;
	++iter;
	valset[1][0] = iter;
	valset[1][1] = hk / 1.5;
	valset[1][2] = CmpDkDiffquotientbyerrH2(fun, x0, valset[1][1]);
	valset[1][3] = valset[1][2] - valset[0][2];
	do
	{
		double dDk, dDk1;
		hk_t = hk / powf(1.5, iter);
		valset[iter][0] = iter + 1;
		valset[iter][1] = hk_t;
		valset[iter][2] = CmpDkDiffquotientbyerrH2(fun, x0, hk_t);
		err = valset[iter][2] - valset[iter - 1][2];
		valset[iter][3] = err;
		if (abs(err) < eps)
		{
			++iter;
			break;
		}
		dDk = valset[iter - 1][2] - valset[iter - 2][2];
		dDk1 = valset[iter][2] - valset[iter - 1][2];
		if (abs(dDk1) > abs(dDk))
		{
			break;
		}
	} while (++iter < N);
}
第二题：
//the D2jk_1 has the 2*h stepsize,and the Djk_1 is h,the k is order of Dk
double CmpDjkbyExtrapolation(double Djk_1, double D2jk_1,const int k)
{
	double val;
	val = (Djk_1 - D2jk_1) / (powf(4, k) - 1);
	return Djk_1 + val;
}
//cmp the Dk with the k is 1
double CmpDkDiffquotientbyerrH2(double (*fun)(double), const double x, const double hk)
{
	double dk;
	dk = fun(x + hk) - fun(x);
	return dk / hk;
}
//construst the Dk matrix,which j row,k col represent the Dk(hj)
//so can cmp every order of Dk by the stepsize hk
//the h0 is the initial stepsize,N is the max iteration times
void CmpDkMatrixbyExtrapolation(double (*fun)(double), double **Dk, double x, const double h0, const int N, double eps)
{
	double hk = h0, err;
	int ord = 1;
	//cmp the D0(h)
	Dk[0][0] = CmpDkDiffquotientbyerrH2(fun, x, hk);
	do
	{
		hk /= 2.;
		Dk[ord][0]= CmpDkDiffquotientbyerrH2(fun, x, hk);
		//cmp the i row val,i is the order of Dk ,the i row have ord elements,as the Dk is N*N
		for (int i = 0; i < ord; ++i)
		{
			Dk[ord][i + 1] = CmpDjkbyExtrapolation(Dk[ord][i], Dk[ord - 1][i], i + 1);
		}
		err = abs(Dk[ord][ord] - Dk[ord - 1][ord - 1]);
		if (err < eps)
		{
			++ord;
			break;
		}
		++ord;
	} while (ord < N);
}

2、牛顿、拉格朗日多项式微分原理实现

  由第一节原理可知，计算导数数值的误差主要来源于计算机的截断误差和舍入误差。其中，当步长太小时，舍入误差会变大；当步长太大时，截断误差会变大，因此会陷入一个步长两难的问题。所以,在进行数值微分计算时要小心处理。当对精度有限的试验数据进行计算时,困难更大。如果必须根据数据集求数值导数,应该先用最小二乘法进行曲线拟合,然后对曲线函数进行微分。因此，我们可以选用拉格朗日多项式和牛顿多项式进行曲线拟合。
  因此，当使用牛顿多项式微分法进行求解的时候，其优点就是可以通过数据集而不必知道具体的函数表达式即可求解导数的较为精确的近似值，因为有的时候知道函数表达式并不是一件容易的事情，因此牛顿多项式在实际问题处理中具有较大的意义。
  其基本流程为：

1. 根据已知的函数自变量值及其对应的函数值进行牛顿多项式的系数求解。
2. 得到导数的近似表达式。值得注意的是，N阶牛顿多项式具有N+1个结点，因此其导数表达式是从$a_1$开始的N阶多项式。
3. 在所选取的函数插值点区间内，利用牛顿多项式进行求解，避免出现外插值的情况。

  因此，以下通过一个实例来具体使用牛顿多项式求解导数近似值。

• 选取函数$f(x)=ln(x)$,利用N+1个结点构造牛顿多项式微分表达式，求解M个取值点的的一阶导数值。

  通过流程图我们可以知道，选取区间$[1,5]$上包括端点的$N+1=51$个结点构造N次牛顿多项式，并将区间内的值带入微分表达式中，通过迭代计算其导数近似值并与真值进行比较，最终得到误差结果。
  其核心函数算法代码为：

//cmp the coe of Newton polynomial from 1 to N.Totally,having N points,save the every difference quotient to DiffTab
//and save the A1 to An to Ak
void CmpNewtonPolyCoe(double** DiffTab, double* Ak, double* xpt, double* ypt, const int N)
{
	double hk;
	//cmp the DiffTab
	//fill the 1st col to the DiffTab
	for (int i = 0; i < N; ++i)
	{
		DiffTab[i][0] = ypt[i];
	}
	//fill the data to the 2nd to Nth col
	for (int col = 1; col < N; ++col)
	{
		for (int row = col; row < N; ++row)
		{
			hk = xpt[row] - xpt[row - col];
			//for each row,have row element,so can fill the every row first
			DiffTab[row][col] = (DiffTab[row][col - 1] - DiffTab[row - 1][col - 1]) / hk;
		}
	}
	for (int i = 0; i < N; ++i)
	{
		Ak[i] = DiffTab[i][i];
	}
}
//cmp the product without k,and the N is the num of data，also the index of Ak
double CmpProdSumvalinN(double x, double* xpt, const int N)
{
	double prod, prodsum;
	prodsum = 0;
	for (int i = 0; i < N; ++i)
	{
		prod = 1;
		for (int j = 0; j < i; ++j)
		{
			prod *= (x - xpt[j]);
		}
		for (int j = i + 1; j < N; ++j)
		{
			prod *= (x - xpt[j]);
		}
		prodsum += prod;
	}
	return prodsum;
}
//cmp the Derivative of xxs,and save it to Derivative,leng is the length of xxs and Derivative
//the N is the num of the points,so Ak has N-1 items
void CmpApproxDerivative(double* Ak, double *xxs, const int leng, double* xpt,const int N, double *Derivative)
{
	double Pval, sumXk, x;
	for (int index = 0; index < leng; ++index)
	{
		Pval = Ak[1];
		x = xxs[index];
		for (int i = 2; i <= N; ++i)
		{
			//cmp the product-sum
			sumXk = CmpProdSumvalinN(x, xpt, i);
			Pval += Ak[i] * sumXk;
		}
		Derivative[index] = Pval;
	}
}

---

三、结果分析

1、中心差分和理查森外推法实例分析

  通过表（1）（2）可以直观的看出，在相同迭代次数的情况下，精度为$O(h^4)$比精度为$O(h^2)$的中心差分公式的误差更小，并且迭代次数更少。除此之外，其误差的区别是以数量级的形式相差，因此精度为$O(h^4)$比精度为$O(h^2)$的中心差分公式求解导数近似值更加优越。通过表（3）可以直观看出任意一阶中心差分公式以及任意步长的导数求解近似值，最终导数的近似值收敛于$1.2286$，然而函数在$x_0$点处的导数值真值为$1.228697$，因此可以看出理查森外推法相较于另外两种方法更接近于真值，因此在计算时具有更优越的特性。

2、牛顿、拉格朗日多项式微分实例分析

   通过表（4）的数据可以直观地看出，在区间$[1,5]$内选取51个结点构建牛顿多项式，求解出来的导数近似值在除端点外具有非常高的精度，其误差数量级之大以至于可以忽略，因此可以看出利用内插法进行求解是具有极高的精度的。可以发现，其误差最大值出现在端点处，且越靠近端点处其误差逐渐增加。可能原因是牛顿多项式是通过多项式拟合函数的，其效果仅仅为拟合函数值，而多项式的导数具有发散性，因此无法像样条插值那样通过特殊的条件保证导数的连续性以及拟合性，而多项式的导数往往在边界会出现迅速的变化，因此会出现如实验数据所表现的情况。综上所述，在对特定区间进行牛顿多项式导数求解时应当注意其插值点区间的选取，避免出现边缘失真的情况。

---

四、结论

  通过分析求解导数近似解的原理，我们可以得到几点结论。第一，对于利用中心差分公式求解导数近似解时，其阶数越高，误差就会越小，且随着步长的减小更快趋近于0，但是对于不同阶数的中心差分公式其误差最小的步长不相同，因此需要通过推导大致确定其步长。对于其迭代终止条件，我们还应当考虑其截断误差性，即需要预判导数的发散情况从而选择终止迭代的时机。第二，当想利用更高阶中心差分公式求解一阶导数时，理查森外推法可以有效地减小运算量，并且可以得到小于最大阶数的任意阶任意步长求解的导数值，但是前提是需要考虑初始步长的设置以及容差的选择。最后，当仅仅知道部分函数值点的时候，我们可以利用拉格朗日多项式和牛顿多项式进行导数近似值的求解。其中拉格朗日多项式可以推导出更多的不同精度的不同阶导数的近似值表达式。然而一般会利用牛顿多项式的易于求导的特点进行一阶导数的求解，其精度极高，但应当注意边缘发散的情况。

---

声明：本系列《数值计算方法》所有章节源代码均为作者编写，大家可以自行下载，仅供学习交流使用，欢迎大家评论留言或者私信交流，请勿用于任何商业行为。其中，各章实验数据结果也在资源链接中，大家可以自行实验对照，欢迎大家批评指正！文件中每个算法均由作者进行初步测试，部分算法可直接用于工程开发作为模块参考。

各章算法源代码（C++）