数字图像处理与MATLAB 第四章学习笔记
第四章 图像复原与重建
图像复原技术主要目的是以预先确定的目标来改善图像,大部分属于客观处理,面向退化模型,并采用相反的过程进行处理,以便恢复出原图像。
图像增强技术基本上是一种探索性过程,即根据人类视觉系统的生理和心理特征来设计一种改善图像的方法。
4.1 图像退化/复原处理的模型
在本章,退化过程被建模为一个退化函数和一个加性噪声项,对一幅图像f(x, y)处理产生退化后的图像g(x, y):g(x, y) = H[f(x, y)]+η(x, y)。给定g(x, y)和关于退化函数H的一些知识以及关于加性噪声项η(x, y)的一些知识后,图像复原的目的就是获得源图像的一个估计 f ^ ( x , y ) \hat f (x,y) f^(x,y)。通常,我们希望这一估计尽可能地接近原始输入图像,并且H和η知道的信息越多所得到的 f ^ ( x , y ) \hat f (x,y) f^(x,y)越接近f(x, y)。
若H是一个线性、空间不变的过程,则空间域中的退化图像可由式给出: g ( x , y ) = h ( x , y ) ★ f ( x , y ) + η ( x , y ) g(x, y)=h(x, y)★f(x, y)+η(x, y) g(x,y)=h(x,y)★f(x,y)+η(x,y)。式中,h(x, y)是该退化函数的空间表示。
空间域的卷积和频率域的乘法组成了一个傅里叶变换对,所以可以用等价的频率域来写出前面的模型:G(u, v)=H(u, v)F(u, v)+N(u, v)。式中,用大写字母表示的是空间域中相应项的傅里叶变换。退化函数F(u, v)有时称为光传递函数(OTF)(源于光学系统的傅里叶分析)。在空间域中,h(x, y)称为点扩散函数(PSF)(来源:对于任何类型的输入,让h(x, y)作用域一个点光源来得到退化的特征)。OTF和PSF是一个傅里叶变换对,工具箱函数otf2psf和psf2otf用于在OTF和PSF之间相互转换。
由于线性、空间不变的退化函数H可以由卷积来建模,所以退化处理有时也被称为PSF与图像卷积。类似的,复原处理有时也被称为去卷积。
4.2 噪声模型
模拟噪声特性和影响的能力是图像复原的核心。
4.2.1 使用函数imnoise对图像添加噪声
函数imnoise可以用噪声污染一幅图像,语法:g=imnoise(f, type, parameters),其中f是输入图像。该函数在给图像添加噪声之前将图像转换为区间[0, 1]上的double类。语法形式如下表:
| 语法 | 注释 |
|---|---|
| g=imnoise(f, ‘gaussian’, m, var) | 将均值为吗、方差为var的高斯噪声添加到图像f上。默认值是均值为0、方差0.01的噪声。 |
| g=imnoise(f, ‘localvar’, V) | 将均值为0、局部方差为V的高斯噪声添加到图像f上,其中V是大小与f相同的数组,它在每个点包含了期望的方差值。 |
| g=imnoise(f, ‘localvar’, image_intensity, var) | 将均值为0的高斯噪声添加到图像f上,其中噪声的局部方差var是图像f的灰度值的函数。自变量image_intensity和var是大小相同的向量,plot(image_intensity, var)绘制出噪声方差和图像灰度间的函数关系。向量image_intensity必须是[0, 1]上的归一化灰度值。 |
| g=imnoise(f, ‘salt%pepper’, d) | 用椒盐噪声污染图像f,其中d是噪声密度(包含噪声值的图像区域的百分比),大约有d*numel(f)个像素受到影响,默认噪声密度0.05。 |
| g=imnoise(f, ‘speckle’, var) | 使用方程g=f+n.*f将乘性噪声添加到图像f上,其中n是均值为0、方差为var的均匀分布的随机噪声,var默认值0.04。 |
| g=imnoise(f, ‘poisson’) | 由数据生成泊松噪声,而不将人为噪声添加到数据中。为服从泊松统计,uint8、uint16类图像的灰度必须对应于光子数(或其他量子信息)。当每个像素中的光子数大于65535(但小于 1 0 12 10^{12} 1012)时需要使用双精度图像,灰度值在0~1之间变化,并且对应于光子的数量除以 1 0 12 10^{12} 1012。 |
4.2.2 使用规定分布生成空间随机噪声
空间噪声是随机数,由概率密度函数(PDF)或等效的累积分布函数(CDF)来表征。
许多随机数生成器以区间(0, 1)上的一个均匀CDF来表达随机数的生成问题为基础。有些情形下所选的基本随机数生成器是均值为0、方差为1的高斯随机数生成器。
本节的基本方法是概率论的一个著名结果:若w是在区间(0,1)上均匀分布的一个随机变量,则通过求解方程 z = F − 1 ( w ) z=F^{-1}(w) z=F−1(w)可得到一个具有规定CDF和F的随机变量z,该结果也可以等效表述为求方程 F ( z ) = w F(z)=w F(z)=w的解。
使用均匀随机数生成具有规定分布的随机数
假设有一个区间(0, 1)上的均匀随机数w的生成器,并假设要用该生成器生成具有瑞利CDF的随机数z,有如下形式: F ( z ) = { 1 − e − ( z − a ) 2 b , z ≥ a 0 , z < a ( b > 0 ) F(z)=\begin{cases} 1-e^{-\frac{(z-a)^2}{b}},z\geq a \\0,z0) F(z)={1−e−b(z−a)2,z≥a0,z<a(b>0)。求出z需要解方程 1 − e − ( z − a ) 2 b = w 1-e^{-\frac{(z-a)^2}{b}}=w 1−e−b(z−a)2=w或 z = a + − b l n ( 1 − w ) z=a+\sqrt{-bln(1-w)} z=a+−bln(1−w)。由于平方根项非负,因此可以确定不会生成小于a的z值,与瑞利CDF的定义所要求的一致。该生成器生成的均匀随机数w可以用在前面的方程中,以便生成一个具有瑞利分布且带有参数a、b的随机变量z。
语句*R=a+sqrt(b×log(1-rand(M, N)));*可以生成一个随机数数组R,rand可以生成区间(0, 1)上的均匀分布随机数。若M=N=1,则该语句由一个具有瑞利分布且以参数a和b来表征的随机变量生成一个单一值。
表达式 z = a + − b l n ( 1 − w ) z=a+\sqrt{-bln(1-w)} z=a+−bln(1−w)有时称为随机数生成方程,因为它确定了生成期望随机数的方式。此情形下可以求出一个解析解,但并不总是可能的,其输出近似于具有给定CDF的随机数。
表4.1 随机变量的生成
| 名称 | 均值和方差 | CDF | 生成器* | |
|---|---|---|---|---|
| 均匀 | p ( z ) = { 1 b − a , 0 ≤ z ≤ b 0 , 其 他 p(z)=\begin{cases} \frac{1}{b-a},0\leq z \leq b \\ 0,其他 \end{cases} p(z)={b−a1,0≤z≤b0,其他 | m = a + b 2 , σ 2 = ( b − a ) 2 12 m=\frac{a+b}{2},\sigma^2=\frac{(b-a)^2}{12} m=2a+b,σ2=12(b−a)2 | F ( z ) = { 0 , z < a z − a b − a , a ≤ z ≤ b 1 , z > b F(z)=\begin{cases} 0,zb\end{cases} F(z)=⎩⎪⎨⎪⎧0,z<ab−az−a,a≤z≤b1,z>b | MATLAB函数rand |
| 高斯 | p ( z ) = 1 2 π b e − ( z − a ) 2 2 b 2 , − ∞ < z < ∞ p(z)=\frac{1}{\sqrt{2\pi}b}e^{-\frac{(z-a)^2}{2b^2}},-\infty |
m = a , σ 2 = b 2 m=a,\sigma^2=b^2 m=a,σ2=b2 | F ( z ) = ∫ − ∞ z p ( v ) d v F(z)=\int_{-\infty}^{z} p(v)dv F(z)=∫−∞zp(v)dv | MATLAB函数randn |
| 对数正态 | p ( z ) = 1 2 π b z e [ l n ( z ) − a ] 2 2 b 2 , z > 0 p(z)=\frac{1}{\sqrt{2\pi}bz}e^{\frac{[ln(z)-a]^2}{2b^2}},z>0 p(z)=2πbz1e2b2[ln(z)−a]2,z>0 | m = e a + ( b 2 2 ) , σ 2 = [ e b 2 − 1 ] e 2 a + b 2 m=e^{a+(\frac{b^2}{2})},\sigma^2=[e^{b^2}-1]e^{2a+b^2} m=ea+(2b2),σ2=[eb2−1]e2a+b2 | F ( z ) = ∫ 0 z p ( v ) d v F(z)=\int_0^z p(v)dv F(z)=∫0zp(v)dv | z = e b N ( 0 , 1 ) + a z=e^{bN(0,1)+a} z=ebN(0,1)+a |
| 瑞利 | p ( z ) = { 2 b ( z − a ) e − ( z − a ) 2 b , z ≥ a 0 , z < a p(z)=\begin{cases} \frac{2}{b}(z-a)e^{-\frac{(z-a)^2}{b}},z\geq a \\0,zp(z)={b2(z−a)e−b(z−a)2,z≥a0,z<a | m = a + π b 4 , σ 2 = b ( 4 − π ) 4 m=a+\sqrt{\frac{\pi b}{4}},\sigma^2=\frac{b(4-\pi)}{4} m=a+4πb,σ2=4b(4−π) | F ( z ) = { 1 − e − ( z − a ) 2 b , z ≥ a 0 , z < a F(z)=\begin{cases} 1-e^{-\frac{(z-a)^2}{b}},z\geq a\\0,zF(z)={1−e−b(z−a)2,z≥a0,z<a | z = a + − b l n [ 1 − U ( 0 , 1 ) ] z=a+\sqrt{-bln[1-U(0,1)]} z=a+−bln[1−U(0,1)] |
| 指数 | p ( z ) = { a e − a z , z ≥ 0 0 , z < 0 p(z)=\begin{cases} ae^{-az},z\geq0\\0,z<0 \end{cases} p(z)={ae−az,z≥00,z<0 | m = 1 a , σ 2 = 1 a 2 m=\frac{1}{a},\sigma^2=\frac{1}{a^2} m=a1,σ2=a21 | F ( z ) = { 1 − e − a z , z ≥ 0 0 , z < 0 F(z)=\begin{cases} 1-e^{-az},z\geq0\\0,z<0\end{cases} F(z)={1−e−az,z≥00,z<0 | z = − 1 a l n [ 1 − U ( 0 , 1 ) ] z=-\frac{1}{a}ln[1-U(0,1)] z=−a1ln[1−U(0,1)] |
| 爱尔兰 | p ( z ) = a b z b − 1 ( b − 1 ) ! e − a z , z ≥ 0 p(z)=\frac{a^bz^{b-1}}{(b-1)!}e^{-az},z\geq0 p(z)=(b−1)!abzb−1e−az,z≥0 | m = b a , σ 2 = b a 2 m=\frac{b}{a},\sigma^2=\frac{b}{a^2} m=ab,σ2=a2b | F ( z ) = [ 1 − e − a z ∑ n = 0 b − 1 ( a z ) n n ! ] , z ≥ 0 F(z)=\big[1-e^{-az}\sum_{n=0}^{b-1}\frac{(az)^n}{n!}\big],z\geq0 F(z)=[1−e−az∑n=0b−1n!(az)n],z≥0 | z 1 = E 1 + E 2 + ⋯ + E b ( E 是 带 参 数 a 的 指 数 随 机 数 ) z_1=E_1+E_2+\dots+E_b(E是带参数a的指数随机数) z1=E1+E2+⋯+Eb(E是带参数a的指数随机数) |
| 椒盐** | p ( z ) = { P p , z = 0 ( 胡 椒 ) P s , z = 2 n − 1 ( 盐 粒 ) 1 − ( P p + P s ) , z = k ( 0 < k < 2 n − 1 ) p(z)=\begin{cases}P_p,z=0(胡椒)\\P_s,z=2^n-1(盐粒)\\1-(P_p+P_s),z=k(0 |
m = ( 0 ) P p + k ( 1 − P p − P s ) + ( 2 n − 1 ) P s m=(0)P_p+k(1-P_p-P_s)+(2^n-1)P_s m=(0)Pp+k(1−Pp−Ps)+(2n−1)Ps σ 2 = ( 0 − m ) 2 P p + ( k − m ) 2 ( 1 − P p − P s ) + ( 2 n − 1 − m ) 2 P s \sigma^2=(0-m)^2P_p+(k-m)^2(1-P_p-P_s)+(2^n-1-m)^2P_s σ2=(0−m)2Pp+(k−m)2(1−Pp−Ps)+(2n−1−m)2Ps | F ( z ) = { 0 , z < 0 P p , 0 ≤ z < k 1 − P s , k ≤ z < 2 n − 1 1 , 2 n − 1 ≤ z F(z)=\begin{cases}0,z<0\\P_p,0\leq z |
带有一些其他逻辑的MATLAB函数rand |
*:N(0,1)表示均值为0、方差为1的均匀(高斯)随机数,U(0, 1)表示区间为(0, 1)的均匀随机数。
**:如正文所解释的那样,椒盐噪声可视为带有三个值的一个随机变量,这三个值依次用于噪声将被应用到的图像;因此均值和方差的意义不同于其他噪声类型,在此包含它们的目的只是为了完整性的需要(均值和方差公式中包含的0表示胡椒噪声假定为0),变量m是噪声将被应用到的数字图像的位数。
一个像素被椒盐噪声污染的概率为 P = P p + P s P=P_p+P_s P=Pp+Ps,P称为噪声密度。
自定义M函数imnoise2可以生成具有上表中CDF的随机数,使用了函数rand,语法A=rand(M, N),生成一个大小为M×N的数组,其值是在(0, 1)之间均匀分布的数;若调用此函数无参数,则rand将生成单个随机数,每次调用时生成的数会发生改变。类似的,函数*A=randn(M, N)*也生成了一个大小为M×N的数组,其元素是具有零均值、单位方差的正态(高斯)数,省略N则默认值为M。该M函数也使用MATLAB函数find,语法形式如下:
I=find(A)%以I形式返回A中所有非零元素的线性索引。若未找到非零元素则find返回一个空矩阵;以格式A(:)来处理数组A,所以I是一个列向量。
[r, c]=find(A)%返回矩阵A中非零元素的行、列索引
[r, c, v]=find(A)%除了返回行、列索引外还以列向量v返回A中的非零值
imnoise2生成的M×N噪声数组R,该数组不以任何方式缩放,且生成的是噪声模式本身(相较于imnoise而言,其生成的是一幅带噪声的图像)。
由椒盐噪声生成的噪声数组有三个值:0是胡椒噪声,1是盐粒噪声,0.5是无噪声。要使这个数组产生作用还需要对其进行进一步处理:例如要污染一幅图像,需要(使用函数find或逻辑索引)找到R中所有值为0的坐标,并把图像中相应坐标处的值置为可能的最小灰度值(通常是0);类似的还需要找到R中所有坐标值为1的坐标,并把图像中相应坐标处的值置为可能的最大灰度值(对于8bit图像通常为255);图像中所有其他像素值不变。
例4.2 使用函数imnoise2所生成数据的直方图
使用imnoise2生成完随机数后,可使用函数hist生成直方图,语法hist(r, bins),bins是容器的数量。
4.2.3 周期噪声
图像中出现的周期噪声通常来自于电气和/或电机干扰,这是本章唯一考虑的噪声。
周期噪声通常是通过频率滤波进行处理,周期噪声模型是一个离散的二维正弦波,方程为:
r ( x , y ) = A s i n [ 2 π u 0 ( x + B x ) / M + 2 π v 0 ( y + B y ) / N ] r(x,y)=Asin[2\pi u_0(x+B_x)/M+2\pi v_0(y+B_y)/N] r(x,y)=Asin[2πu0(x+Bx)/M+2πv0(y+By)/N]
(x∈[0, M-1],y∈[0, N-1],A为振幅, u 0 u_0 u0和 v 0 v_0 v0分别确定关于x、y轴的正弦频率, B x B_x Bx和 B y B_y By是关于原点的相移(输出的正弦波和输入的正弦波信号的相位差称为相移))该方程的DFT是:
R ( u , v ) = j A M N 2 [ e − j 2 π ( u 0 B x / M + v 0 B y / N ) δ ( u + u 0 , v + v 0 ) − e − j 2 π ( u 0 B x / M + v 0 B y / N ) δ ( u − u 0 , v − v 0 ) ] R(u,v)=j\frac{AMN}{2}[e^{-j2\pi(u_0B_x/M+v_0B_y/N)}\delta(u+u_0,v+v_0)-e^{-j2\pi(u_0B_x/M+v_0B_y/N)}\delta(u-u_0,v-v_0)] R(u,v)=j2AMN[e−j2π(u0Bx/M+v0By/N)δ(u+u0,v+v0)−e−j2π(u0Bx/M+v0By/N)δ(u−u0,v−v0)]
(u∈[0, M-1],v∈[0, N-1])。我们看到的是分别位于 ( u + u 0 , v + v 0 ) (u+u_0,v+v_0) (u+u0,v+v0)和 ( u − u 0 , v − v 0 ) (u-u_0,v-v_0) (u−u0,v−v0)的一对复共轭单位冲激(一种持续期极短的信号)。
函数imnoise3接受任意数量的冲击位置(频率坐标),每个冲激位置都有自己的振幅、频率和相移参数,按照前述正弦和计算 r ( x , y ) r(x,y) r(x,y),同时输出各个正弦波之和的傅里叶变换 R ( u , v ) R(u,v) R(u,v)及 R ( u , v ) R(u,v) R(u,v)的谱。正弦波是由给定的冲激位置信息通过反DFT生成,其结果是更加直观且简化了空间噪声模式中频率内容的形象化显示。确定一个冲激的位置只需要一对坐标。要使用ifft2,就需要使用函数ifftshift将居中的R转换为合适的数据排列。
4.2.4 估计噪声参数
周期噪声的参数通常是分析傅里叶谱来估计的,往往会生成频率尖峰,这些尖峰通常可以通过目视来检测,当尖峰非常明显/存在一些干扰频率时就有可能自动分析。
描述直方图形状的主要方法是使用其中心矩(也称均值的矩),定义为 μ n = ∑ i = 0 L − 1 ( z i − m ) n p ( z i ) \mu_n=\sum_{i=0}^{L-1} (z_i-m)^np(z_i) μn=∑i=0L−1(zi−m)np(zi)( z i z_i zi为一个离散随机变量,表示一幅图像的灰度级, p ( z i ) ( i ∈ [ 0 , L − 1 ] ) p(z_i)(i\in[0,L-1]) p(zi)(i∈[0,L−1])是相应的归一化直方图,L是可能的灰度值数量;直方图的一个分量 p ( z i ) p(z_i) p(zi)是灰度值 z i z_i zi出现概率的一个估计,且该直方图可视为灰度PDF的一个离散近似;n是矩的阶,m是均值: m = ∑ i = 0 L − 1 z i p ( z i ) m=\sum_{i=0}^{L-1} z_ip(z_i) m=∑i=0L−1zip(zi))。因为假设直方图是归一化的,其所有分量之和为1,所以可得出 μ 0 = 1 , μ 1 = 0 \mu_0=1,\mu_1=0 μ0=1,μ1=0,二阶矩 μ 2 = ∑ i = 0 L − 1 ( z i − m ) 2 p ( z i ) \mu_2=\sum_{i=0}^{L-1}(z_i-m)^2p(z_i) μ2=∑i=0L−1(zi−m)2p(zi)是方差。
函数statmoments计算均值和n阶中心矩,并以行向量v返回它们(零阶矩恒为1、一阶矩恒为0,所以statmoments会忽略这两个矩),并改为令 v ( 1 ) = m v(1)=m v(1)=m和 v ( k ) = μ k , k ∈ [ 2 , n ] v(k)=\mu_k,k\in[2,n] v(k)=μk,k∈[2,n],语法:[v, unv] = statmoments(p, n),其中p为直方图向量(其分量数量取决于图像类型,uintx类图像即有 2 x 2^x 2x,single和double类分别有 2 8 2^8 28和 2 16 2^{16} 216),n是将要计算的矩的数量;输出向量v包含了归一化矩,向量unv包含了与v相同的矩,但计算时使用的是原始区间的数据。
通常,噪声函数必须直接由给定的一幅或一组带噪图像来估计,方法是尽可能选取图像中一个无特色的背景区域,以便该区域灰度值变化主要由噪声引起。函数roipoly可以选择一个感兴趣区域(ROI),该函数将生成一个多边形ROI,语法B=roipoly(f, c, r),f是感兴趣的图像,c、r是该多边形的顶点的对应(顺序)列坐标和行坐标(已预先规定),顶点坐标原点在左上角,输出B是一幅二值图像,常用作将运算限制在感兴趣区域内的一个模板,大小等于f,ROI之外为0,之内为1。
语法*B=roipoly(f)*可以交互式地(使用鼠标)指定一个多边形地ROI,省略f则该函数将在最后显示的图像上运算,交互行为如下表:
表4.2 函数roipoly的交互选项
| 交互行为 | 描述 |
|---|---|
| 关闭多边形 | 下列机制任选:**1、**将鼠标指针移到多边形的起始顶点上,此时指针变成一个圆圈,单击鼠标任意按钮 **2、**双击鼠标左键,此运算在鼠标指针下方的点处创建一个顶点,并画出一条链接该顶点和起始顶点的线 **3、**单击鼠标右键,画一条链接起始顶点和所选最后顶点的直线,它在鼠标指针下方的点处不创建一个新顶点。 |
| 移动多边形 | 在区域内移动鼠标指针,指针改变为✥,在图像上单击并拖动该多边形 |
| 删除多边形 | 按Backspace、Escape或Delete或在区域内右键单击,从出现的菜单中选择Cancel(若删除ROI则函数将返回空值) |
| 移动一个顶点 | 把指针移到一个顶点上,指针变为圆形,单击并拖动顶点到一个新位置 |
| 添加一个顶点 | 移动鼠标到多边形一条边上,按住A键,指针变为✧,单击左键即可创建新顶点 |
| 删除一个顶点 | 移动鼠标到多边形一个顶点上,指针变为圆圈,右键单击并从菜单上选择Delete vertex。函数roipoly在与所删除顶点相邻的两个顶点之间画一条新的直线。 |
| 设置多边形颜色 | 移动指针到区域边界内任何地方,指针变为✥,单击右键选择Set color |
| 检索顶点坐标 | 移动指针到区域内,变成✥,单击右键选择Copy position,将当前位置复制到剪贴板,位置是一个n×2的数组,该组每一行包含每个顶点的列、行坐标,n是顶点数,坐标系统原点在图像左上角。 |
函数histroi用于计算一个ROI直方图,该ROI顶点由向量c、r指定。程序中使用函数roipoly来复制由c、r定义的多边形区域,语法*[p, npix]=histroi(f, c, r)*。
4.3 仅有噪声的复原——空间滤波
若出现的退化仅是噪声,则其遵循4.1节模型: g ( x , y ) = f ( x , y ) + η ( x , y ) g(x,y)=f(x,y)+\eta(x,y) g(x,y)=f(x,y)+η(x,y)。此时所选的方法是空间滤波。
4.3.1 空间噪声滤波器
函数spfilt用表4.3中列出的任何滤波器执行空间滤波,其中函数imlincomb用于计算输入的线性组合,函数tofloat将输出图像转换为与输入图像相同类别的;语法f=spfilt(g, type, varargin)。
function f = spfilt(g, type, varargin)%如下为注释部分
%SPFILT Performs linear and nonlinear spatial filtering.
% F = SPFILT(G, TYPE, M, N, PARAMETER) performs spatial filtering
% of image G using a TYPE filter of size M-by-N. Valid calls to
% SPFILT are as follows:
%
% F = SPFILT(G, 'amean', M, N) Arithmetic mean filtering.
% F = SPFILT(G, 'gmean', M, N) Geometric mean filtering.
% F = SPFILT(G, 'hmean', M, N) Harmonic mean filtering.
% F = SPFILT(G, 'chmean', M, N, Q) Contraharmonic mean
% filtering of order Q. The
% default Q is 1.5.
% F = SPFILT(G, 'median', M, N) Median filtering.
% F = SPFILT(G, 'max', M, N) Max filtering.
% F = SPFILT(G, 'min', M, N) Min filtering.
% F = SPFILT(G, 'midpoint', M, N) Midpoint filtering.
% F = SPFILT(G, 'atrimmed', M, N, D) Alpha-trimmed mean
% filtering. Parameter D must
% be a nonnegative even
% integer; its default value
% is 2.
%
% The default values when only G and TYPE are input are M = N = 3,
% Q = 1.5, and D = 2.
表4.3 空间滤波器。变量m和n分别表示滤波器跨越的行数和列数
| 滤波器名称 | 公式 | 注释 |
|---|---|---|
| 算术均值 | f ^ ( x , y ) = 1 m n ∑ ( s , t ) ∈ S x y g ( s , t ) \hat{f}(x,y)=\frac{1}{mn} \sum_{(s,t)\in S_{xy}}g(s,t) f^(x,y)=mn1∑(s,t)∈Sxyg(s,t) | 用工具箱函数w=fspecial(‘average’, [m,n])和f = imfilter(g,w)实现 |
| 几何均值 | f ^ ( x , y ) = [ ∏ ( s , t ) ∈ S x y g ( s , t ) ] 1 m n \hat{f}(x,y)=[\prod_{(s,t)\in S_{xy}}g(s,t)]^{\frac{1}{mn}} f^(x,y)=[∏(s,t)∈Sxyg(s,t)]mn1 | 该非线性滤波器使用函数gmean来实现(如上) |
| 调和均值 | f ^ ( x , y ) = m n ∑ ( s , t ) ∈ S ( x , y ) 1 g ( s , t ) \hat{f}(x,y)=\frac{mn}{\sum_{(s,t)\in S_{(x,y)}}\frac{1}{g(s,t)}} f^(x,y)=∑(s,t)∈S(x,y)g(s,t)1mn | 该非线性滤波器使用函数harmean来实现(同上) |
| 逆调和均值 | f ^ ( x , y ) = ∑ ( s , t ) ∈ S x y g ( s , t ) Q + 1 ∑ ( s , t ) ∈ S x y g ( s , t ) Q \hat{f}(x,y)=\frac{\sum_{(s,t)\in S_{xy}}g(s,t)^{Q+1}}{\sum_{(s,t)\in S_{xy}}g(s,t)^Q} f^(x,y)=∑(s,t)∈Sxyg(s,t)Q∑(s,t)∈Sxyg(s,t)Q+1 | 使用函数charmean来实现(同上) |
| 中值 | f ^ ( x , y ) = m e d i a n ( s , t ) ∈ S x y { g ( s , t ) } \hat{f}(x,y)=median_{(s,t)\in S_{xy}}\{{g(s,t)}\} f^(x,y)=median(s,t)∈Sxy{g(s,t)} | 用工具箱函数*medfilt2: f=medfilt2(g,[m n],‘symmetric’)*实现 |
| 最大值 | f ^ ( x , y ) = m a x ( s , t ) ∈ S x y { g ( s , t ) } \hat{f}(x,y)=max_{(s,t)\in S_{xy}}\{{g(s,t)}\} f^(x,y)=max(s,t)∈Sxy{g(s,t)} | 用工具箱函数*imdilate: f=imdilate(g, ones(m,n))*实现 |
| 最小值 | f ^ ( x , y ) = m i n ( s , t ) ∈ S x y { g ( s , t ) } \hat{f}(x,y)=min_{(s,t)\in S_{xy}}\{{g(s,t)}\} f^(x,y)=min(s,t)∈Sxy{g(s,t)} | 用工具箱函数*imerode: f=imerode(g, ones(m,n))*实现 |
| 中点 | f ^ ( x , y ) = 1 2 [ m a x ( s , t ) ∈ S x y { g ( s , t ) } + m i n ( s , t ) ∈ S x y { g ( s , t ) } ] \hat{f}(x,y)=\frac{1}{2}[max_{(s,t)\in S_{xy}}\{{g(s,t)}\}+min_{(s,t)\in S_{xy}}\{{g(s,t)\}}] f^(x,y)=21[max(s,t)∈Sxy{g(s,t)}+min(s,t)∈Sxy{g(s,t)}] | 由最大、最小滤波结果之和的0.5倍实现 |
| 修正 α \alpha α均值 | f ^ ( x , y ) = 1 m n − d ∑ ( s , t ) ∈ S x y g r ( s , t ) \hat{f}(x,y)=\frac{1}{mn-d}\sum_{(s,t)\in S_{xy}}g_r(s,t) f^(x,y)=mn−d1∑(s,t)∈Sxygr(s,t) | 在 S x y S_{xy} Sxy中,删除 g ( s , t ) g(s,t) g(s,t)的 d / 2 d/2 d/2个最低像素值和 d / 2 d/2 d/2个最高像素值。函数 g r ( s , t ) g_r(s,t) gr(s,t)表示邻域中剩下的 m n − d mn-d mn−d个像素,用函数alphatrim实现(同上) |
4.3.2 自适应空间滤波器(中值)
设 S x y S_{xy} Sxy是一幅子图像,该子图像的中心在将被处理图像中的位置(x,y),详细解释如下:
z m i n = S x y 中 的 最 小 灰 度 值 z m a x = S x y 中 的 最 大 灰 度 值 z m e d = S x y 中 的 灰 度 中 值 z x y = 坐 标 ( x , y ) 处 的 灰 度 值 z_{min}=S_{xy}中的最小灰度值\\ z_{max}=S_{xy}中的最大灰度值\\ z_{med}=S_{xy}中的灰度中值\\ z_{xy}=坐标(x,y)处的灰度值 zmin=Sxy中的最小灰度值zmax=Sxy中的最大灰度值zmed=Sxy中的灰度中值zxy=坐标(x,y)处的灰度值
自适应中值滤波算法使用两个处理层次(表示为层次A和层次B):
层 次 A : 若 z m i n < z m e d < z m a x , 则 转 至 层 次 B , 否 则 增 大 窗 口 尺 寸 。 若 窗 口 尺 寸 ≤ S m a x , 则 重 复 层 次 A , 否 则 输 出 z m e d 层 次 B : 若 z m i n < z x y < z m a x , 则 输 出 z x y , 否 则 输 出 z m e d 层次A:若z_{min}
其中 S m a x S_{max} Smax表示自适应滤波器窗口允许的最大尺寸。层次A最后一步的另种选择是输出 z x y z_{xy} zxy而不是输出中值。
M函数adpmedian可以实现该算法,语法f=adpmedian(g, Smax),g是将被滤波的图像,Smax是自适应滤波器创就的最大允许尺寸。
4.4 使用频率域滤波降低周期噪声
滤除周期噪声(类冲激)的主要方法是使用陷波带阻滤波。具有Q个陷波对的陷波带阻滤波器通式为: H N R ( u , v ) = ∏ k = 1 Q H k ( u , v ) H − k ( u , v ) H_{NR}(u,v)=\prod_{k=1}^Q H_k(u,v)H_{-k}(u,v) HNR(u,v)=∏k=1QHk(u,v)H−k(u,v),其中 H k ( u , v ) H_k(u,v) Hk(u,v)和 H − k ( u , v ) H_{-k}(u,v) H−k(u,v)是高通滤波器,其中心分别是 ( u k , v k ) (u_k,v_k) (uk,vk)和 ( − u k , − v k ) (-u_k,-v_k) (−uk,−vk)。这些平移后的中心是相对于频率矩形中心 ( M / 2 , N / 2 ) (M/2,N/2) (M/2,N/2)所规定的,滤波器公式如下: D k ( u , v ) = [ ( u − M / 2 − u k ) 2 + ( v − N / 2 − v k ) 2 ] 1 2 D_k(u,v)=[(u-M/2-u_k)^2+(v-N/2-v_k)^2]^{\frac{1}{2}} Dk(u,v)=[(u−M/2−uk)2+(v−N/2−vk)2]21和 D − k ( u , v ) = [ ( u − M / 2 + u k ) 2 + ( v − N / 2 + v k ) 2 ] 1 2 D_{-k}(u,v)=[(u-M/2+u_k)^2+(v-N/2+v_k)^2]^{\frac{1}{2}} D−k(u,v)=[(u−M/2+uk)2+(v−N/2+vk)2]21。
函数cnotch可以生成这些类型的陷波带阻滤波器。
4.5 退化函数建模
图像复原的一个主要退化就是图像模糊,场景和传感器的模糊可以使用空间或频率域的低通滤波器来建模;另一个重要退化模型是在图像获取时传感器和场景之间的均匀线性运动生成的图像模糊,可以用函数fspecial建模,语法PSF=fspecial(‘motion’, len, theta),调用fspecial结果是返回PSF,用来近似摄像机线性移动len个像素的效果(theta单位是度,是相对于正水平轴按顺时针方向测得的,默认值0;len默认值9)。
函数checkerboard可生成一个测试图案用于测试滤波所用方法的合理性,因为其大小可以缩放而不影响其主要特征,语法:C=checkerboard(NP, M, N)(NP是每个正方形一条边上的像素数,M是行数,N是列数(省略则默认M=N);M省略则M=N=8,NP省略则默认10)。图像默认图像时左半部亮正方形白色、右半部亮正方形灰色;生成全白色亮正方形可以使用K=checkerboard(NP, M, N)>0.5;图像默认double类,范围[0,1].
函数pixeldup可以实现通过像素复制来放大图像(用于显示的目的),语法B=pixeldup(A, m, n), 结果是将A的每个像素在垂直方向上复制m次、水平方向上复制n次(n值省略则为m)。
4.6 直接逆滤波
用来复原一幅退化图像的最简单的方法是在4.1节的模型中忽略噪声项,并形成估计: F ^ ( u , v ) = G ( u , v ) H ( u , v ) \hat{F}(u,v)=\frac{G(u,v)}{H(u,v)} F^(u,v)=H(u,v)G(u,v),然后取 F ^ ( u , v ) \hat{F}(u,v) F^(u,v)的傅里叶反变换得到图像的相应估计,称为逆滤波。
若考虑噪声,则估计变为 F ^ ( u , v ) = F ( u , v ) + N ( u , v ) H ( u , v ) \hat{F}(u,v)=F(u,v)+\frac{N(u,v)}{H(u,v)} F^(u,v)=F(u,v)+H(u,v)N(u,v),可知即使准确知道了 H ( u , v ) H(u,v) H(u,v)也不能恢复 F ( u , v ) F(u,v) F(u,v),因此不能恢复未被退化的原图像 f ( x , y ) f(x,y) f(x,y);噪声分量是随机函数,因此其傅里叶变换 N ( u , v ) N(u,v) N(u,v)是未知的;即使噪声项 N ( u , v ) N(u,v) N(u,v)可以忽略,使用为0的 H ( u , v ) H(u,v) H(u,v)的值来除它也会支配复原估计。
4.7 维纳滤波
维纳滤波器寻找统计误差函数 e 2 = E { ( f − f ^ ) 2 } e^2=E\{{(f-\hat{f})^2\}} e2=E{(f−f^)2}的一个最小估计 f ^ \hat{f} f^, E E E是期望值算子, f f f是未退化图像,此式在频率域中的解是 F ^ ( u , v ) = [ 1 H ( u , v ) ∣ H ( u , v ) 2 ∣ ∣ H ( u , v ) ∣ 2 + S η ( u , v ) / S f ( u , v ) ] G ( u , v ) \hat{F}(u,v)=\bigg[\frac{1}{H(u,v)}\frac{|H(u,v)^2|}{|H(u,v)|^2+S_\eta(u,v)/S_f(u,v)}\bigg]G(u,v) F^(u,v)=[H(u,v)1∣H(u,v)∣2+Sη(u,v)/Sf(u,v)∣H(u,v)2∣]G(u,v);其中 H ( u , v ) H(u,v) H(u,v)是退化函数, ∣ H ( u , v ) ∣ 2 = H ∗ ( u , v ) H ( u , v ) |H(u,v)|^2=H^*(u,v)H(u,v) ∣H(u,v)∣2=H∗(u,v)H(u,v), H ∗ ( u , v ) = H ( u , v ) H^*(u,v)=H(u,v) H∗(u,v)=H(u,v)的复共轭, S η ( u , v ) = ∣ N ( u , v ) ∣ 2 = S_\eta(u,v)=|N(u,v)|^2= Sη(u,v)=∣N(u,v)∣2=噪声的功率谱, S f ( u , v ) = ∣ F ( u , v ) ∣ 2 = S_f(u,v)=|F(u,v)|^2= Sf(u,v)=∣F(u,v)∣2=未退化图像的功率谱,比例式 S η ( u , v ) / S f ( u , v ) S_\eta(u,v)/S_f(u,v) Sη(u,v)/Sf(u,v)称为噪信功率比;对于u和v的所有相关值,噪声功率谱为0,则比例式直接变为0,该滤波器则变为逆滤波器。
平均噪声功率定义为 η A = 1 M N ∑ u ∑ v S η ( u , v ) \eta_A=\frac{1}{MN}\sum_u\sum_vS_\eta(u,v) ηA=MN1∑u∑vSη(u,v),平均图像功率定义为 f A = 1 M N ∑ u ∑ v S f ( u , v ) f_A=\frac{1}{MN}\sum_u\sum_vS_f(u,v) fA=MN1∑u∑vSf(u,v),其中M、N分别表示图像数组和噪声数组的行数和列数;其比值 R = η A f A R=\frac{\eta_A}{f_A} R=fAηA也是一个标量,有时被用来代替函数 S η ( u , v ) / S f ( u , v ) S_\eta(u,v)/S_f(u,v) Sη(u,v)/Sf(u,v)生成一个常量数组。
用一个常量数组来代替 S η ( u , v ) / S f ( u , v ) S_\eta(u,v)/S_f(u,v) Sη(u,v)/Sf(u,v)就得到了所谓参数维纳滤波器,可以对直接逆滤波产生重大改进。
函数deconvwnr可以实现维纳滤波,语法形式及对应结果如下表:(g代表退化图像,frest表示复原图像)
| 语法 | 结果 |
|---|---|
| frest=deconvwnr(g, PSF) | 假设噪信比为0,即可得到逆滤波器 |
| frest=deconvwnr(g, PSF, NSPR) | 假设噪信功率比已知,不是常量就是数组,用于实现参数维纳滤波器,此时NSPR为标准输入 |
| frest=deconvwnr(g, PSF, NACORR, FACORR) | 假设噪声和未退化图像的自相关函数NACORR和FACORR是已知的。 deconvwnr的这种形式使用 η \eta η和 f f f的自相关代替这些函数的功率谱 |
由相关定理可知 ∣ F ( u , v ) ∣ 2 = ℑ [ f ( x , y ) ☆ f ( x , y ) ] |F(u,v)|^2=ℑ[f(x,y)☆f(x,y)] ∣F(u,v)∣2=ℑ[f(x,y)☆f(x,y)](☆表示相关运算,ℑ表示傅里叶变换):表明通过计算功率谱的傅里叶变换,可以得到自相关函数 f ( x , y ) ☆ f ( x , y ) f(x,y)☆f(x,y) f(x,y)☆f(x,y),也可套进噪声的自相关。
若复原的图像中出现因算法使用离散傅里叶变换引入的振铃,则在调用函数edgetaper之前使用函数deconvwnr是有帮助的;语法J=edgetaper(I, PSF)。该函数利用点扩散函数PSF模糊输入图像I的边缘,输出图像J就是图像I及其模糊版本的加权和。此加权数组由PSF的自相关函数所决定,在其中心处取J=I,在接近边缘处取J等于I的模糊版本。
4.8 由投影重建图像
CT是图像处理在医学中的主要应用之一,本节将介绍由一系列一维投影重建图像。
4.8.1 背景
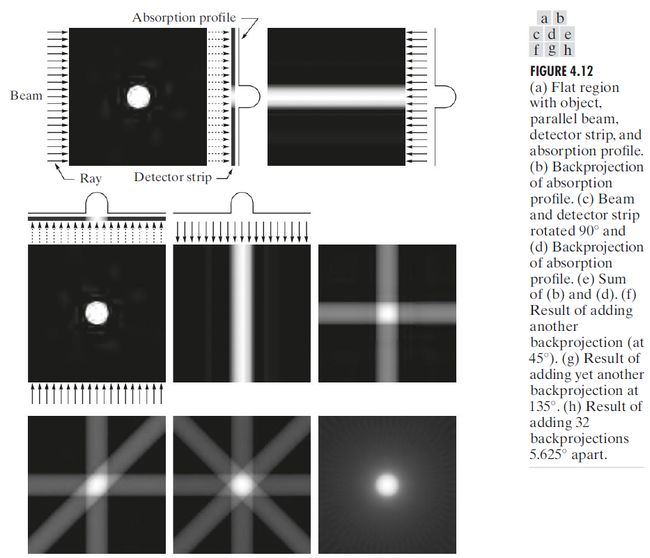
最大吸收点出现在区域中心时,射线束在此处遇到物体的最长路径,此点的吸收剖面就是我们具有的这一物体的全部信息。
由单个投影无法确定沿射线路径处理的物体数量,但是可以基于这种部分信息开始重建工作,方法是沿射线射入方向把吸收剖面投影回去(称为反投影),可以生成一幅二维数字图像;当把射线束/检测器排列旋转90°并重复投影过程,把得到的投影加在原投影图像上,即可得到包含目标区域的图像,其中包含目标区域的灰度是图像其他主要分量灰度的2倍。
给定一组以为投影和这些投影所取的角度,X射线断层成像的基本问题是由生成的投影来重建该区域的一幅图像(称为一个切片);实践中可以通过平移垂直于直线束/检测器对的物体可以得到多个切片,堆叠这些切片可以再现这些扫描物体内部的三维视图。
4.8.2 平行射线束投影和雷登变换
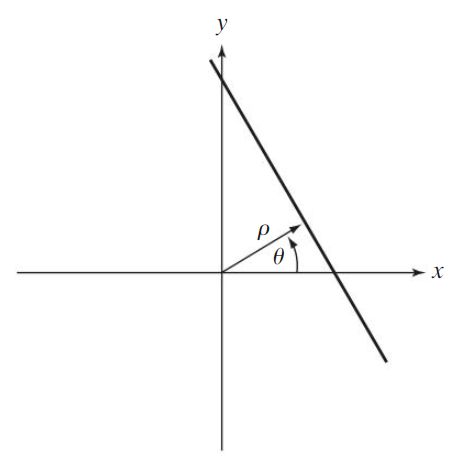
笛卡尔坐标系(xOy坐标系)中的一条直线可以使用斜截式 y = a x + b y=ax+b y=ax+b来描述,也可以用其法线形式来表示: x c o s ( θ ) + y s i n ( θ ) = ρ xcos(\theta)+ysin(\theta)=\rho xcos(θ)+ysin(θ)=ρ。
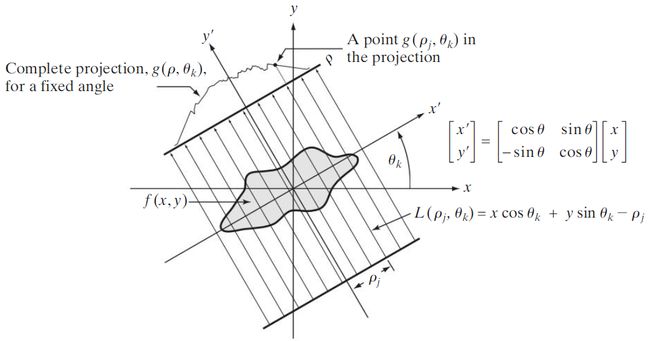
投影剖面上任意一点的坐标 ( ρ j , θ k ) (\rho_j, \theta_k) (ρj,θk)由沿直线 x c o s θ k + y s i n θ k = ρ j xcos\theta_k+ysin\theta_k=\rho_j xcosθk+ysinθk=ρj的射线和给出。射线和是一个线积分,由下式给出: g ( ρ j , θ k ) = ∫ − ∞ ∞ ∫ − ∞ ∞ f ( x , y ) δ ( x c o s θ k + y s i n θ k − ρ j ) d x d y g(\rho_j,\theta_k)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\delta(xcos\theta_k+ysin\theta_k-\rho_j)dxdy g(ρj,θk)=∫−∞∞∫−∞∞f(x,y)δ(xcosθk+ysinθk−ρj)dxdy。
式中使用了冲激函数 δ \delta δ的取样特性,即若 δ \delta δ的参量不为0,则右边的等式为0,意味着积分仅沿直线 x c o s θ k + y s i n θ k = ρ j xcos\theta_k+ysin\theta_k=\rho_j xcosθk+ysinθk=ρj计算。若考虑 ρ \rho ρ和 θ \theta θ的所有值,则上式可以推广为 g ( ρ , θ ) = ∫ − ∞ ∞ ∫ − ∞ ∞ f ( x , y ) δ ( x c o s θ k + y s i n θ k − ρ j ) d x d y g(\rho,\theta)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(x,y)\delta(xcos\theta_k+ysin\theta_k-\rho_j)dxdy g(ρ,θ)=∫−∞∞∫−∞∞f(x,y)δ(xcosθk+ysinθk−ρj)dxdy。
给出沿xy平面中沿任意一条直线的 f ( x , y ) f(x,y) f(x,y)的投影(线积分)的这一公式,就是雷登变换。如上图所示,任意角度 θ k \theta_k θk的完整投影是 g ( ρ , θ k ) g(\rho,\theta_k) g(ρ,θk),且此函数是在雷登变换中插入 θ k \theta_k θk得到的。
前述积分的离散近似可以写为 g ( ρ , θ ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) δ ( x c o s θ + y s i n θ − ρ ) g(\rho,\theta)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)\delta(xcos\theta+ysin\theta-\rho) g(ρ,θ)=∑x=0M−1∑y=0N−1f(x,y)δ(xcosθ+ysinθ−ρ),其中 x x x、 y y y、 ρ \rho ρ和 θ \theta θ是离散变量(实践中不常用)。固定 θ \theta θ使 ρ \rho ρ变化,可知此表达式生成 f ( x , y ) f(x,y) f(x,y)沿着由这两个参数的值定义的直线的所有值的和;上述条件下增大 ρ \rho ρ的所有值以覆盖该图像将产生一个投影;改变 θ \theta θ并重复前述过程将产生另一个投影,以此类推。
断层成像的目的是由给定的一组投影恢复 f ( x , y ) f(x,y) f(x,y),通过反投影每个一维投影,由这些特殊投影来创建一幅图像可以实现这一任务,通过对这些图像求和可以得到最终的结果。
得到反投影图像的表达式的过程:从固定 θ k \theta_k θk值的全部投影 g ( ρ , θ k ) g(\rho,\theta_k) g(ρ,θk)的单个点 g ( ρ j , θ k ) g(\rho_j,\theta_k) g(ρj,θk)开始,将直线 L ( ρ j , θ k ) L(\rho_j,\theta_k) L(ρj,θk)复制到图像上即可,其中沿该条直线的所有点的值是 g ( ρ j , θ k ) g(\rho_j,\theta_k) g(ρj,θk);对投影信号中的所有 ρ j \rho_j ρj值重复这一过程(同时保证 θ \theta θ值固定为 θ k \theta_k θk),即可得到 f θ k ( x , y ) = g ( ρ , θ k ) = g ( x c o s θ k + y s i n θ k , θ k ) f_\theta{_k}(x,y)=g(\rho,\theta_k)=g(xcos\theta_k+ysin\theta_k,\theta_k) fθk(x,y)=g(ρ,θk)=g(xcosθk+ysinθk,θk)。该公式适用于任何角度值,因此可以把由(在角度 θ \theta θ得到的)单个反投影形成的图像写为 f θ ( x , y ) = g ( x c o s θ + y s i n θ , θ ) f_\theta(x,y)=g(xcos\theta+ysin\theta,\theta) fθ(x,y)=g(xcosθ+ysinθ,θ)。对所有反投影图像进行积分,可得到最后的图像: f ( x , y ) = ∫ 0 π f θ ( x , y ) d θ f(x,y)=\int_0^\pi f_\theta(x,y)d\theta f(x,y)=∫0πfθ(x,y)dθ,其中积分只在半周上进行,因为在区间 [ 0 , π ] [0,\pi] [0,π]上得到的投影和在区间 [ π , 2 π ] [\pi,2\pi] [π,2π]上得到的投影相同。
离散情形下该积分变成对所有反投影图像的求和: f ( x , y ) = ∑ θ = 0 π f θ ( x , y ) f(x,y)=\sum_{\theta=0}^\pi f_\theta(x,y) f(x,y)=∑θ=0πfθ(x,y),其中变量现在是离散值。
函数radon和前面的公式可以用来生成下图,但会出现难以忍受的模糊结果。
4.8.3 傅里叶切片定理与滤波反投影
g ( ρ , θ ) g(\rho,\theta) g(ρ,θ)关于 ρ \rho ρ的一维傅里叶变换如下: G ( ω , θ ) = ∫ − ∞ ∞ g ( ρ , θ ) e − j 2 π ω ρ d ρ G(\omega,\theta)=\int_{-\infty}^{\infty}g(\rho,\theta)e^{-j2\pi\omega\rho}d\rho G(ω,θ)=∫−∞∞g(ρ,θ)e−j2πωρdρ,其中 ω \omega ω是频率变量,该表达式适用于固定的 θ \theta θ值。
计算断层成像的一个基本结果称为傅里叶切片定理,定理表明一个投影的傅里叶变换是得到该投影区域的二维变换的一个切片,即 G ( ω , θ ) = [ F ( u , v ) ] u = ω c o s θ , v = ω s i n θ = F ( ω c o s θ , ω s i n θ ) G(\omega,\theta)=[F(u,v)]_{u=\omega cos\theta,v=\omega sin\theta}=F(\omega cos\theta,\omega sin\theta) G(ω,θ)=[F(u,v)]u=ωcosθ,v=ωsinθ=F(ωcosθ,ωsinθ)。其中 F ( u , v ) F(u,v) F(u,v)仍是 f ( x , y ) f(x,y) f(x,y)的二维傅里叶变换,结果如下图示意(图4.11)。
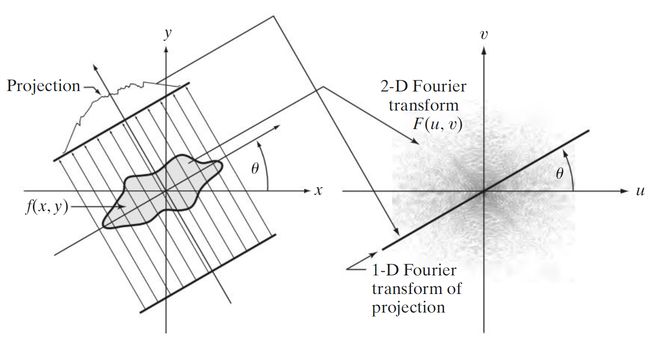
使用傅里叶切片定理推导频率域中 f ( x , y ) f(x,y) f(x,y)的表达式
给定 F ( u , v ) F(u,v) F(u,v),使用傅里叶反变换可得到 f ( x , y ) f(x,y) f(x,y): f ( x , y ) = ∫ − ∞ ∞ ∫ − ∞ ∞ F ( u , v ) e j 2 π ( u x + v y ) d u d v f(x,y)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(u,v)e^{j2\pi(ux+vy)}dudv f(x,y)=∫−∞∞∫−∞∞F(u,v)ej2π(ux+vy)dudv。
若令 u = ω c o s θ u=\omega cos\theta u=ωcosθ和 v = ω s i n θ v=\omega sin\theta v=ωsinθ,则 d u d v = ω d ω d θ dudv=\omega d\omega d\theta dudv=ωdωdθ。
然后由傅里叶切片定理有 f ( x , y ) = ∫ 0 2 π ∫ 0 ∞ G ( ω , θ ) e j 2 π ω ( x c o s θ + y s i n θ ) ω d ω d θ f(x,y)=\int_{0}^{2\pi}\int_{0}^{\infty}G(\omega,\theta)e^{j2\pi\omega(xcos\theta+ysin\theta)}\omega d \omega d\theta f(x,y)=∫02π∫0∞G(ω,θ)ej2πω(xcosθ+ysinθ)ωdωdθ
通过将这个积分拆成两个表达式,一个用于区间 [ 0 , π ] [0,\pi] [0,π]的 θ \theta θ,另一个用于 [ π , 2 π ] [\pi,2\pi] [π,2π]的 θ \theta θ,并使用 G ( ω , θ + π ) = G ( − ω , θ ) G(\omega,\theta+\pi)=G(-\omega,\theta) G(ω,θ+π)=G(−ω,θ)可以将前面的积分表示为 f ( x , y ) = ∫ 0 π ∫ − ∞ ∞ ∣ ω ∣ G ( ω , θ ) e j 2 π ω ( x c o s θ + y s i n θ ) d ω d θ f(x,y)=\int_0^{\pi}\int_{-\infty}^{\infty}|\omega|G(\omega,\theta)e^{j2\pi\omega(xcos\theta+ysin\theta)}d\omega d\theta f(x,y)=∫0π∫−∞∞∣ω∣G(ω,θ)ej2πω(xcosθ+ysinθ)dωdθ。
关于 ω \omega ω的积分,如 ρ \rho ρ一样, x c o s θ + y s i n θ xcos\theta+ysin\theta xcosθ+ysinθ项为常数,因此前述公式可表示为 f ( x , y ) = ∫ 0 π [ ∫ − ∞ ∞ ∣ ω ∣ G ( ω , θ ) e j 2 π ω ] r h o d ω ] ρ = x c o s θ + y s i n θ d θ f(x,y)=\int_0^\pi \big[\int_{-\infty}^{\infty}|\omega|G(\omega,\theta)e^{j2\pi\omega]rho}d\omega \big]_{\rho=xcos\theta+ysin\theta}d\theta f(x,y)=∫0π[∫−∞∞∣ω∣G(ω,θ)ej2πω]rhodω]ρ=xcosθ+ysinθdθ;内部表达式是一个一维傅里叶变换,只是附加了 ∣ ω ∣ |\omega| ∣ω∣项(一个一维滤波器函数,在两个方向上有无限扩展的V型,不可积)。理论上此问题可以使用广义 δ \delta δ函数来处理。
得到完全的反投影图像 f ( x , y ) f(x,y) f(x,y)步骤
·计算每个投影的一维傅里叶变换
·用滤波函数 ∣ ω ∣ |\omega| ∣ω∣乘以每个傅里叶变换(此滤波器必须乘以一个合适的窗函数)
·得到第二步导致的每个滤波后的变换的一维傅里叶反变换
·对第三步所得到的所有以为反变换积分(求和)得到 f ( x , y ) f(x,y) f(x,y)
因为使用了一个滤波器,所以刚给出的方法可称为由滤波投影重建图像;实践中数据是离散的,因此所有频率域计算是用一维FFT算法实现的。
4.8.4 滤波器实现
使用一个窗函数乘以斜坡滤波器可以使滤波器的拖尾逐渐消失,从而在高频处降低其幅度。斜坡滤波器本身的持续时间(宽度)受限于用来生成该滤波器的频率点数
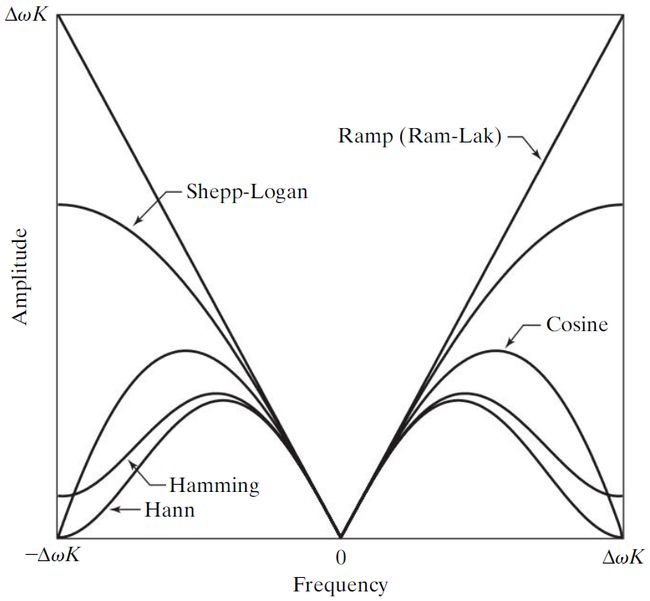
正弦窗的传递函数为 H s ( ω ) = s i n ( π ω / 2 Δ ω K ) π ω / 2 Δ ω K , ω = 0 , ± Δ ω , ± 2 Δ ω , ⋯ , ± K Δ ω H_s(\omega)=\frac{sin(\pi\omega/2\Delta\omega K)}{\pi\omega/2\Delta\omega K},\omega=0,\pm\Delta\omega,\pm2\Delta\omega,\cdots,\pm K\Delta\omega Hs(ω)=πω/2ΔωKsin(πω/2ΔωK),ω=0,±Δω,±2Δω,⋯,±KΔω。其中K是滤波器其中的频率间隔数(点数-1);类似的,余弦窗的传递函数为 H c ( ω ) = c o s π ω 2 Δ ω K H_c(\omega)=cos\frac{\pi\omega}{2\Delta\omega K} Hc(ω)=cos2ΔωKπω。
汉明窗和汉宁窗的传递函数相同,都是 H ( ω ) = c + ( c − 1 ) c o s π ω 2 Δ ω K H(\omega)=c+(c-1)cos\frac{\pi\omega}{2\Delta\omega K} H(ω)=c+(c−1)cos2ΔωKπω,c=0.54时为汉明窗,c=0.5时为汉宁窗(差别是在汉宁窗张端点为0,汉宁窗有一个小偏移,但这两个窗得到的结果视觉上几乎无法辨别)。
下图4.13为用前面的窗函数乘以斜坡滤波器生成的反投影滤波器。
4.8.5 使用扇形射线束滤波反投影的重建
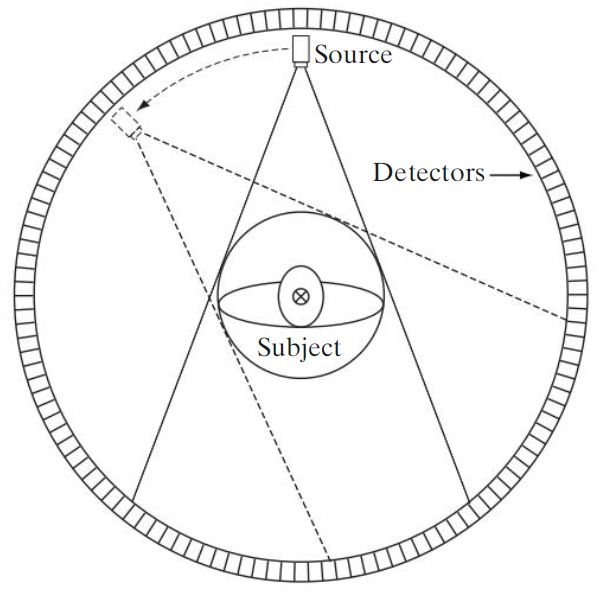
下图显示了典型的扇形射线束扫描几何,其使用一个检测器环,在此排列下X射线围绕被测物体旋转;对于每个水平位移增量,完整的射线源旋转生成一幅切片图像;垂直于检测器屏幕移动被测物体可生成一组切片图像,将这些图像堆叠在一起就可以生成被测物体扫描截面的三维表示。
推导扇形射线束的相关公式重要方面是在扇形射线束与平行几何间建立一一对应的关系;从一个对应关系到另一个对应关系,会涉及变量的简单变化。
4.8.6 函数radon
该函数用于对给定的二维矩形数组生成一组平行射线投影,语法R=radon(I, theta),其中I是一个二维数组,theta是角度值的一维数组;投影包含在R的列中,生成的投影数等于数组theta的角度数。生成的投影长到足以在射线束旋转时跨越观察的宽度。当射线垂直于矩形数组的主对角线时就会出现这种视图。换句话说,对于一个大小为M×N的数组,投影的最小长度时 ( M 2 + N 2 ) 1 / 2 (M^2+N^2)^{1/2} (M2+N2)1/2。
由函数radon返回的实际长度要稍大于为每个像素的单位面积计算的主对角线长度。
更一般的语法为*[R, xp]=radon(I, theta)* ,其中xp包含沿 x ′ x' x′轴的坐标值,即图4.11中的 ρ \rho ρ值,其值用于标注图轴。
在CT算法模拟中,用来生成谢普—洛根头部幻影的语法为:P=phantom(def, n),其中def是一个指定所生成头部幻影类型的字符串,n是行数和列数(默认值256),有效值如下表:
| 有效值 | 解释 |
|---|---|
| ‘Shepp-Logan’ | 计算机断层研究人员广泛使用的测试图像,对比度很低 |
| ‘Modified Shepp-Logan’ | 谢普—洛根头部幻影的变体,对比度得到了改进 |
4.8.7 函数iradon
函数iradon用以不同角度得到的一组给定来投影重建一幅图像(切片),即计算雷登反变换。滤波器直接在频率域设计,然后乘以投影的FFT;在滤波前为减少空间域混淆并加快FFT的计算速度,所有投影都零填充为2的幂的大小。语法I=iradon(R, theta, interp, filter, frequency_scaling, output_size。参数如下表:
| 参数 | 解释 |
|---|---|
| R | 反投影数据。其中列是以角度从左到右渐增的函数来组织的一维反投影 |
| theta | 描述取投影的角度(单位为度)。既可以是包含角度的一个向量,也可以是指定的D_theta(投影间的角度增量)的一个标量。若theta是一个向量,则它必须包含等于投影间隔的角度;若theta是一个指定D_theta的标量,则要假定投影取自角度m*D_theta,其中 m ∈ [ 0 , s i z e ( R , 2 ) − 1 ] m\in[0,size(R,2)-1] m∈[0,size(R,2)−1];若输入是空矩阵,则D_theta默认值为180/size(R,2)。 |
| interp | 字符串,定义生成最终重建图像的内插方法,主要值见表4.4 |
| filter | 指定滤波反投影计算中所用的滤波器。所支持的滤波器见图4.13,在函数iradon指定它们的字符串列在表4.5中;若指定了选项*‘none’*则重建时不执行滤波 |
| frequency_scaling | 是区间 ( 0 , 1 ] (0,1] (0,1]内的一个标量,通过重新标定频率来修改滤波器,默认值1。若函数值小于1,则滤波器被压缩到归一化频率区间 [ 0 , f r e q u e n c y − s c a l i n g ] [0,frequency-scaling] [0,frequency−scaling];函数值之上的所有频率置0。 |
| output_size | 标量,指定重建图像中的行数和列数。若未指定output_size,则其大小由投影长度决定:output_size=2×floor(size(R,1)/(2×sqrt(2)));若指定函数值,则iradon重建图像中较小或较大的一部分,但不会改变数据的标定。若投影用函数radon计算,则重建图像的大小可能与原图像的大小不同。 |
表4.4 函数iradon中所用的内插方法
| 方法 | 描述 |
|---|---|
| ‘nearest’ | 最近邻内插 |
| ‘linear’ | 线性内插(默认) |
| ‘cubic’ | 三次内插 |
| ‘spline’ | 样条内插 |
表4.5 函数iradon支持的滤波器
| 方法 | 描述 |
|---|---|
| ‘Ram-Lak’ | 是4.8.4节讨论过的斜坡滤波器,其频率响应是$ |
| ‘Shepp-Logan’ | 用一个函数sinc乘以Ram-Lak滤波器生成的滤波器 |
| ‘Cosine’ | 用一个函数cosine乘以Ram-Lak滤波器生成的滤波器 |
| ‘Hamming’ | 用一个汉明窗乘以Ram-Lak滤波器生成的滤波器 |
| ‘Hann’ | 用一个汉宁窗乘以Ram-Lak滤波器生成的滤波器 |
| ‘None’ | 不执行滤波 |
默认的线性内插产生的结果与三次和样条内插产生的结果,视觉上并无多大区别,只是线性内插速度更快。
4.8.8 处理扇形射线束数据
已知扇形射线束数据后工具箱会先把扇形射线束转换为平行射线束,然后使用前面的平行射线束方法得到反投影。
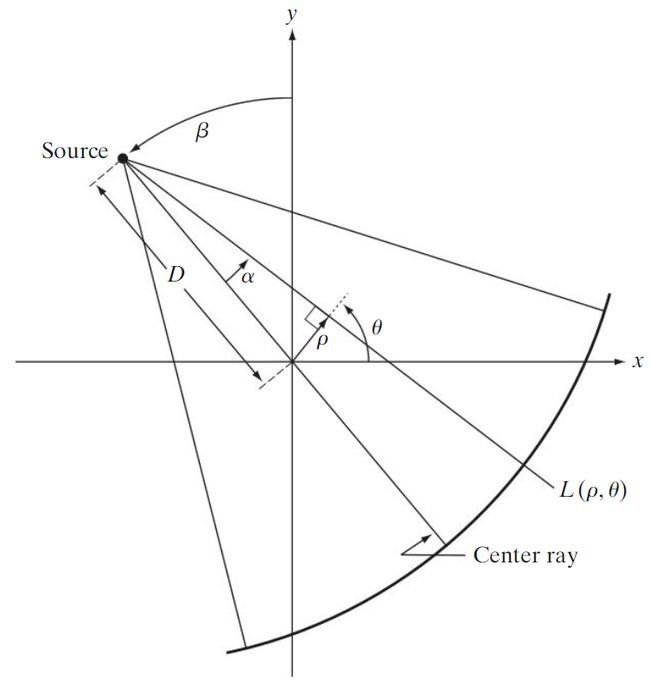
如图4.18为一个基本的扇形射线束成像几何,其中检测器排列在一个圆弧上,并且假定射线源的角度增量是相等的。令 p f a n ( α , β ) p_{fan}(\alpha,\beta) pfan(α,β)表示扇形射线束投影,其中 α \alpha α是特定检测器关于中心射线的角度坐标, β \beta β是射线源关于y轴的角度位移。(扇形射线束中的一束射线可以表示为一条直线 L ( ρ , θ ) L(\rho,\theta) L(ρ,θ))。
平行射线束和扇形射线束可以通过如下表达式联系起来: p f a n ( α , β ) = p p a r ( ρ , θ ) = p p a r ( D s i n α , α + β ) p_{fan}(\alpha,\beta)=p_{par}(\rho,\theta)=p_{par}(Dsin\alpha,\alpha+\beta) pfan(α,β)=ppar(ρ,θ)=ppar(Dsinα,α+β)( p p a r ( ρ , θ ) p_{par}(\rho,\theta) ppar(ρ,θ)是对应的平行射线束投影)。
令 Δ β \Delta\beta Δβ是连续扇形射线束投影间的角度增量,并令 Δ α \Delta\alpha Δα是射线间的角度增量,因此它决定了每个投影中的样本数。利用约束条件 Δ β = Δ α = γ \Delta\beta=\Delta\alpha=\gamma Δβ=Δα=γ,然后对m和n的某些整数值, β = m γ \beta=m\gamma β=mγ和 α = n γ \alpha=n\gamma α=nγ,可以写出 p f a n ( n γ , m γ ) = p p a r ( D s i n n γ , n γ + m γ ) p_{fan}(n\gamma,m\gamma)=p_{par}(Dsin\ n\gamma,n\gamma+m\gamma) pfan(nγ,mγ)=ppar(Dsin nγ,nγ+mγ)。此公式指出,第m个射线投影中的第n条射线等于第 m + n m+n m+n个平行投影中的第n条射线; D s i n n γ Dsin\ n\gamma Dsin nγ项说明从扇形射线束投影转换为平行投影不是均匀采样的,采样间隔 Δ α \Delta\alpha Δα和 Δ β \Delta\beta Δβ太粗将导致模糊、振铃和混淆等问题。
函数fanbeam可以生成扇形射线束投影,语法B=fanbeam(g, D, param1, val1, param2, val2, …)(g是包含将被投影物体的图像,D是从扇形射线束的顶点到旋转中心的距离(单位为像素))。假定旋转中心是图像的中心,规定D大于g直径的一半,则有D=K×sqrt(size(g, 1)^2 + size(g, 2)^2)/2(K是大于1的常数)。该函数的参数和值在表4.6中。
表4.6 fanbeam函数中所用的参数和值
| 参数 | 描述和值 |
|---|---|
| ‘FanRotationIncrement’ | 指定扇形射线束投影的旋转角度增量(单位为度),有效值是正的实标量,默认值为1 |
| ‘FanSensorGeometry’ | 指定如何等间隔地安排传感器的字符串,有效值’arc’(默认值)和’line’。 |
| ‘FanSensorSpacing’ | 指定扇形射线束传感器间距的一个正的实标量,若为几何则指定’arc’,则说明该值是以度为单位的角度间距;若指定为’line’则说明该值为线性间距。两种情况下默认值都为1 |
B的每一列包含扇形射线束传感器每旋转一个角度得到的样本。B中的列数由扇形旋转增量决定,默认情况下B有360列;行数由传感器数量决定,函数fanbeam通过计算对任意旋转角度覆盖全部图像所需要的涉嫌条数,来求出传感器的数量。
函数ifanbeam可用于由给定的一组扇形射线束投影来得到滤波后的反投影图像,语法I = ifanbeam(B, D, …, param1, val1, param2, val2,…)(B是扇形射线束投影矩阵,D是从扇形射线束顶点到旋转中心的距离(单位为像素))。参数和有效值列在表4.7中。
表4.7 函数ifanbeam中所用的参数和值
| 参数 | 描述和值 |
|---|---|
| ‘FanCoverage’ | 指定射线束旋转的区间。有效值’cycle’和’minimal’,前者指处在整个区间[0,360°]内旋转,后者指出描述物体所需的最小区间,并由此在B中生成投影 |
| ‘FanRotationIncrement’ | 解释同表4.6中的函数fanbeam |
| ‘FanSensorGeometry’ | 解释同表4.6中的函数fanbeam |
| ‘FanSensorSpacing’ | 解释同表4.6中的函数fanbeam |
| ‘Filter’ | 有效值在表4.5中,默认值’Ram-Lak’ |
| ‘FrequencyScaling’ | 解释同函数iradon |
| ‘Interpolation’ | 有效值在表4.4中,默认值’linear’ |
| ‘OutputSize’ | 指定重建图像中行数和列数的一个标量。若函数值未被指定,则ifanbeam自动求出大小;反之ifanbeam重建图像的一个较小或较大部分,但数据的标定不变 |
函数fan2para可将扇形射线束数据转换为平行射线束数据,语法:P=fan2para(F, D, param1, val1, param2, val2,…)(F是数组,其列是扇形射线束投影;D是从扇形射线束顶点到旋转中心的距离,用于生成扇形投影)。有效值如下表。
表4.8 函数fan2para中所用的参数和值
| 参数 | 说明和值 |
|---|---|
| ‘FanCoverage’ | 解释同表4.7中的函数ifanbeam |
| ‘FanRotationIncrement’ | 解释同表4.6中的函数fanbeam |
| ‘FanSensorGeometry’ | 解释同表4.6中的函数fanbeam |
| ‘FanSensorSpacing’ | 解释同表4.6中的函数fanbeam |
| ‘Interpolation’ | 有效值在表4.3中,默认值’linear’ |
| ‘ParallelCoverage’ | 指定旋转区间:'cycle’表示平行数据覆盖360°,‘halfcyle’(默认值)表示平行数据覆盖180° |
| ‘ParallelRotationIncrement’ | 指定平行射线束角度增量(单位为度)的一个正的实标量。若该参数未包含在函数参量中,则假定增量与扇形射线束旋转角度增量相同 |
| ‘ParallelSensorSpacing’ | 指定平行射线束传感器间隔(单位为像素)的一个正实标量。若该参数未包含在函数参量中,则假定间隔是均匀的,其通过对扇形角度说明的区间取样来给出 |
函数para2fan与函数fan2para过程相反,语法:F=para2fan(P, D, param1, val1, param2, val2,…)(P是一个数组,其列包含平行投影;D和之前一样)。有效值如下表。
表4.9 函数para2fan中所用的参数和值
| 参数 | 说明和值 |
|---|---|
| ‘FanCoverage’ | 解释同表4.7中的函数ifanbeam |
| ‘FanRotationIncrement’ | 规定扇形射线束投影旋转角度增量(单位为度)的一个正实标量。若’FanCoverage’是’cycle’,则该函数值必须是360°的倍数;若未指定该参数,则其与平行射线束旋转角度的增量相同 |
| ‘FanSensorGeometry’ | 解释同表4.6中的函数fanbeam |
| ‘FanSensorSpacing’ | 若该值被指定为’arc’或’line’,则其解释同表4.6中的函数fanbeam;若该参数未包含在函数参量中,则默认使用’ParallelSensorSpacing’提供的最小值,这样,若’FanSensorGeometry’是’arc’,则该函数值是180/PI×ASIN(PSPACE/D),其中PSPACE是’ParallelSensorSpacing’的值;若’FanSensorGeometry’是’line’,则该函数值是D×ASIN(PSPACE/D) |
| ‘Interpolation’ | 有效值在表4.4中,默认值’linear’ |
| ‘ParallelCoverage’ | 指定旋转区间:'cycle’表示平行数据覆盖360°,‘halfcyle’(默认值)表示平行数据覆盖180° |
| ‘ParallelRotationIncrement’ | 指定平行射线束角度增量(单位为度)的一个正的实标量。若该参数未包含在函数参量中,则假定增量与扇形射线束旋转角度增量相同 |
| ‘ParallelSensorSpacing’ | 指定平行射线束传感器间隔(单位为像素)的一个正实标量。若该参数未包含在函数参量中,则假定间隔是均匀的,其通过对扇形角度说明的区间取样来给出 |