人工智能知识全面讲解：垃圾邮件克星——朴素贝叶斯算法

6.1 什么是朴素贝叶斯
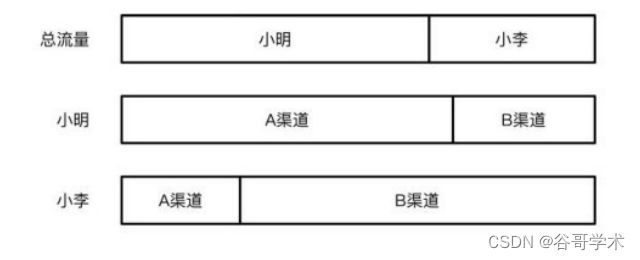
6.1.1 一个流量预测的场景
某广告平台接到小明和小李两家服装店的需求，准备在A、B两个线上渠道
投放广告。因为小明和小李两家店都卖女装，属于同一行业相同品类的广告，
所以在 A、B两个渠道面向的不同用户前只会展示其中一家。一个月以后，从
点击率来看小明的服装店占了A、B两个渠道总流量的65%，小李服装店占剩?
35%的流量。小明服装店的总流量中只有30%的流量是在B渠道中获得的，而小
李服装店在B渠道获得的流量占总流量的75%，如图6-1所示。现在因广告平台
与A渠道合作到期的缘故，投放的渠道只剩? B 渠道，请你预测接?来一段时
间，小明与小李哪一家服装店的流量会更高？
学习完决策树算法以后，聪明的读者都会跃跃欲试。有些读者认为只要找
到这两家服装店的受众以及这个渠道的人群特点，就能构造一棵决策树解决这
个问题。如果以这种方式做，我们需要收集大量的样本数据以及特征维度，才
能构建一棵比较靠谱的决策树。如果我们的目的仅仅是弄清楚哪家店的流量会
更高，那有没有更简单的方法，只借助现有的信息就能解决这个问题呢？

图6-1 广告系统的流量

在机器学习领域还有一种更简单、高效的分类算法可以帮助我们解决这个
问题，那就是朴素贝叶斯分类（Naive Bayesian Classi?ier）算法。
6.1.2 朴素贝叶斯登场
贝叶斯分类是一类分类算法的总称，这类算法均以“贝叶斯定理”为基
础，以“特征条件独立假设”为前提。而朴素贝叶斯分类是贝叶斯分类中最常
见的一种分类方法，同时它也是最经典的机器学习算法之一。在很多场景?处
理问题直接又高效，因此在很多领域有着广泛的应用，如垃圾邮件过滤、文本
分类与拼写纠错等。同时对于产品经理来说，贝叶斯分类法是一个很好的研究
自然语言处理问题的切入点。
朴素贝叶斯分类是一种十分简单的分类算法，说它十分简单是因为它的解
决思路非常简单，即对于给出的待分类项，求解在某些条件?各个类别出现的
概率，哪个最大，就认为此待分类项属于哪个类别。举个形象的例子，若我们
走在街上看到一个黑皮肤的外国友人，让你来猜这位外国友人来自哪里，十有
八九你会猜是从非洲来的，因为黑皮肤人种中非洲人的占比最多，虽然黑皮肤
的外国人也有可能是美洲人或者亚洲人。但是在没有其他可用信息的情况?，
我们会选择出现的概率最高的类别，这就是朴素贝叶斯的基本思想。
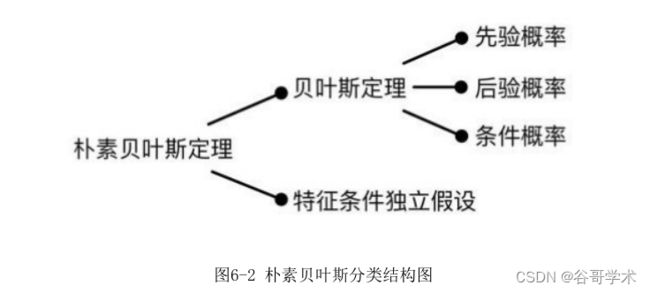
值得注意的是，朴素贝叶斯分类并非瞎猜，也并非没有任何理论依据。它
是以贝叶斯理论和特征条件独立假设为基础的分类算法。想要弄明白算法的原
理，首先需要理解什么是“特征条件独立假设”以及“贝叶斯定理”，而贝叶
斯定理又牵涉“先验概率”“后验概率”及“条件概率”的概念，如图 6-2
所示，虽然概念比较多但是都比较容易理解，?面我们逐个?细介绍。 

特征条件独立假设是贝叶斯分类的基础，意思是假定该样本中每个特征与
其他特征都不相关。例如在预测信用卡客户逾期的例子中，我们会通过客户的
月收入、信用卡额度、房车情况等不同方面的特征综合判断。两件看似不相关
的事情实际上可能存在内在的联系，就像蝴蝶效应一样。一般情况?，银行批
给收入较高的客户的信用卡额度也比较高。同时收入高也代表这个客户更有能
力购买房产，所以这些特征之间存在一定的依赖关系，某些特征是由其他特征
决定的。然而在朴素贝叶斯算法中，我们会忽略这种特征之间的内在关系 ，
直接认为客户的月收入、房产与信用卡额度之间没有任何关系，三者是各自独
立的特征。
接?来我们重点理解什么是“理论概率”与“条件概率”，以及“先验概
率”与“后验概率”之间的区别。
6.2 朴素贝叶斯如何计算
6.2.1 理论概率与条件概率
首先我们进行一个小实验。假设将一枚质地均匀的硬币抛向空中，理论
上，因为硬币的正反面质地均匀，落地时正面朝上或反面朝上的概率都是
50%。这个概率不会随着抛掷次数的增减而变化，哪怕抛了10次结果都是正面
朝上，那?一次正面朝上的概率仍然是50%。
但在实际测试中，如果我们抛100次硬币，则正面朝上和反面朝上的次数
通常不会恰好都是50次。有可能出现40次正面朝上和60次反面朝上的情况，也
有可能出现35次正面朝上和65次反面朝上的情况。只有我们一直抛，抛了成千
上万次，硬币正面朝上与反面朝上的次数才会逐渐趋向于相等。
因此，“正面朝上和反面朝上各有50%的概率”这句话中的概率是理论上
的客观概率。只有抛掷次数足够多时，才会达到这种理想中的概率。在理论概
率?，尽管抛10次硬币，前面5次都是正面朝上，第6次是反面朝上的概率仍然
是50%。但是在实际中，抛过硬币的人都有这样的感觉，如果出现连续5次正面
朝上的情况，那么?一次是反面朝上的可能性极大，大到什么程度？有没有什
么方法可以求出实际的概率呢？
为了解决这个问题，一位名叫托马斯·贝叶斯（Thomas Bayes）的数学家
发明了一种方法，用于计算“在已知条件?，另外一个事件发生”的概率。该
方法要求我们先预估一个主观的先验概率，再根据后续观察到的结果进行调
整，随着调整次数的增加，真实的概率会越来越精确。这句话怎么理解呢？我
们通过一个坐地铁的例子解释这句话的含?。
深圳地铁一号线从车公庙站出发至终点站共有18站，每天早上小林要从车
公庙站出发经过5个站到高新园站上班，如图6-3所示。

 

某天早高峰时段，小林被站立的人群遮挡住视线并且戴着耳机?不到报站
的内容，因此他不知道列车是否到达高新园站。如果?一站列车到站时，他直
接出站，理论上他正好到高新园站的概率只有1/18，出对站的概率非常小。这
时候小林恰巧在人群中看到一个同事，他正走出站台。小林心想，尽管不知道
这个同事要去哪里，但在早高峰时段，同事去公司的概率显然更高。因此在获
得这个有效信息后，小林跟随出站，正好到达高新园站。这种思考方式就是贝
叶斯定理的思考方式。
6.2.2 引入贝叶斯定理
在概率论与统计学中，贝叶斯定理描述了一个事件发生的可能性，这个可
能性是基于事先掌握的一些与该事件相关的情况而推测的。假设癌症是否会发
病与每个人的年龄有关，如果使用贝叶斯定理，当我们知道一个人的年龄时，
就可以更准确地评估他癌症发病的概率。也就是说，贝叶斯理论是指根据一个
已发生事件的概率，计算另一个事件的发生概率。从数学上，贝叶斯理论可以
表示为：

 

● P(B)表示发生B事件的概率，即小林到高新园站的概率。
● P(A)表示发生A事件的概率，即小林的同事出站的概率。
● P(B|A)表示在A事件已经发生的情况?B事件会发生的概率，即同事出
站的时候，小林正好到高新园站的概率。
● P(A|B)表示在B事件已经发生的情况?A事件会发生的概率，即小林到
达高新园站，同事出站的概率。
这时候我们再来看贝叶斯定理，这个公式说明了两个互换的条件概率之间
的关系，它们通过联合概率关联起来。在这种情况?，若知道P(A|B)的值，就
能够计算P(B|A)的值。因此贝叶斯公式实际上阐述了这么一个事情，如图6-4
所示。 

我们可以通过文氏图加深对贝叶斯定理的理解，如图6-5所示。

 

 在上述例子中，小林刚好在早高峰时段看到同事出站，代表出现了新的信
息。就像上图中已知黑点已经落入A区域了，由于A区域大部分区域与B区域相
交，因此推断黑点也在B区域的概率很大。我们想获得的结果其实是P(B|A)，
即我们想知道，在考虑了一些现有的因素后，这个随机事件会以多大概率出
现。参考这个概率结果，在很多事情上我们都可以有针对性地做出决策。
我们需要同时知道P(B)、P(A|B)与P(A)，才能算出目标值P(B|A)，但是
P(A)的值似乎比较难求。仔细想一想，P(A)与 P(B)之间似乎没有任何关联，
两者本身就是独立事件，无论 P(B)的值是大还是小，P(A)都是固定的分母。
也就是说，我们计算P(A)各种取值的可能性并不会对各结果的相对大小产生影
响，因此可以忽略 P(A)的取值。假设P(A)的取值为m，P(B)的可能取值为b1、
b2或者b3，已知：
P（b1）=o，P（b2）=p，P（b3）=q，
P（A|b1）=x，P（A|b2）=y，P（A|b3）=z
那么计算P(B|A)时，分别会得到结果：

且由于P(b1|A)、P(b2|A)与P(b3|A)三者之和一定为1，因此可以得出
ox+py+qz=m。即使m的值不知道也没关系，因为ox、py、qz的值都是可以计算
出来的，所以m的值自然也就知道了。剩?的工作就是计算P(B)、P(A|B)，而
这两个概率必须要通过我们手上有的数据集来进行估计。
关于贝叶斯算法有一段小插曲。贝叶斯算法被发明后有接近200年的时间
无人问津，因为经典统计学在当时完全能够解决客观上能够解释的简单概率问
题，而且相比需要靠主观判断的贝叶斯算法，显然当时的人们更愿意接受建立
在客观事实上的经典统计学，他们更愿意接受一个硬币无论抛多少次后正反面
朝上的概率都是 50%的事实。
但我们的生活中还存在很多无法预知概率的复杂问题，例如台风侵袭、地
震等。经典统计学在面对复杂问题时，往往无法获得足够多的样本数据，导致
其无法推断总体规律。总不能说每天预测台风来的概率都是 50%，只有来或者
不来两种情况。数据的稀疏性令贝叶斯定理频频碰壁，随着近代计算机技术的
飞速发展，对数据的大量运算不再是困难的事情，贝叶斯算法才被人们重新重
视起来。
6.2.3 贝叶斯定理有什么用
讲到这里有读者可能会问，虽然贝叶斯定理模拟了人类思考的过程，但是
它又能够帮助我们解决什么样的问题呢？我们先来看一个一讲到贝叶斯定理必
定会提到的经典案例。
在疾病检测领域，假设某种疾病在所有人群中的感染率是 0.1%，医院现
有的技术对于该疾病检测的准确率能够达到 99%。也就是说，在已知某人已经
患病的情况?，有 99%的可能性检测为阳性；而正常人去检查有 99%的可能性
是正常的，如果从人群中随机抽一个人去检测，医院给出的检测结果为阳性，
则这个人实际得病的概率是多少？
也许很多读者都会脱口而出是“99%”。但真实的得病概率其实远低于
此，原因在于很多读者将先验概率和后验概率搞混了。如果用A表示这个人患
有该疾病，用B表示医院检测的结果是阳性，那么P(B|A)=99%表示的是，“已
知一个人已经得病的情况?医院检测出阳性的概率”。而我们现在问的
是，“对于随机抽取的这个人，在已知检测结果为阳性的情况?这个人患病的
概率”，即P(A|B)，通过计算可得P(A|B)=9%。所以即使被医院检测为阳性，
实际患病的概率其实还不到 10%，有很大可能是假阳性。因此需要通过复诊，
引入新的信息，才有更大的把握确诊。通过以上例子可以看出，生活中我们经
常会把先验概率与后验概率弄混淆，从而得出错误的判断 。贝叶斯定理可以
帮我们理清概率的先后条件之间的逻辑关系，得到更精确的概率。
我们常常遇到这样的场景。当与友人聊天时，一开始可能不知道他要说什
么，但是他说了一句话之后，你就能猜到接?来他要讲什么内容。友人给的信
息越多，我们越能够推断出他想表达的意思，这也是贝叶斯定理的思考方式。
贝叶斯定理得以广泛应用是因为它符合人类认知事物的自然规律。我们并非生
?来就知道一切事情的内在规律，在大多数时候，我们面对的是信息不充分、
不确定的情况，这个时候我们只能在有限资源的情况?，做出决定，再根据后
续的发展进行修正。
实际上，这个定理的核心思想对产品经理如何思考问题也有很大的启发，
一方面我们要搞清楚需求场景中的先验概率是什么，后验概率是什么，不要被
数据的表象蒙蔽了双眼。另一方面我们可以借助贝叶斯定理搭建一个思考的框
架，在这个框架中需要不断地调整我们对某事物的看法，在一系列的新事情被
证实后，才形成比较稳定、正确的看法。
当我们的脑子里有新想法出现时，在大多数情况?，我们只能根据经验大
概判断某个产品靠谱不靠谱。投入市场中反响有多大没有人能够说清楚，因此
很多时候我们需要尝试，需要做一个简单的版本投入市场上快速验证自己的想
法，然后不断想办法获得“事件 B”，不断增加新产品的成功率，这样我们的
产品才有可能获得成功。因此“小步快跑，快速迭代”才是提升容错率最好的
办法。
6.3 朴素贝叶斯的实际应用
6.3.1 垃圾邮件的克星
朴素贝叶斯算法与我们前面学习的回归算法、决策树算法都不太相同。回
归和决策树算法都是实际可以直接应用的算法。朴素贝叶斯算法虽然实现简
单，但是它有一个很重要的前提：假设属性之间相互独立，这个假设在现实应
用中往往是不成立的。因为这个前提的限制导致贝叶斯算法在很长一段时间内
只能用于特征较少、特征之间的相关性较小的场景，一旦属性个数变多或者属
性之间的关联变大分类的效果就会急剧?降。
这种局面非常像目前一些前沿技术的处境，同样是有技术有解决方案，但
是没有找到合适的应用场景，因此没法大展身手。得益于近代自然语言处理领
域的快速发展，人们逐渐发现朴素贝叶斯算法非常适合用于处理文本类的信
息，例如垃圾邮件检测、社区违规信息检测与文档分类等方面。主要原因在于
文本单词之间的关联性很小，基本可以假设为相互独立，因此贝叶斯算法在文
本方面的应用有显著效果。
大概在10年前，每天我们打开邮箱都会发现大量的广告邮件，淹没了重要
的邮件，这让很多用户苦不堪言。聪明的产品经理发现了这个痛点，于是马上
想到可以设定规则过滤掉标题中带有一些特定词语的邮件，直到现在还有很多
邮箱保留了这样的功能。但是狡猾的商家总是变着法躲避关键词的检测，因此
这种方法过滤的效果并不好。如果更进一步，每遇到一种新出现的垃圾邮件种
类就设定过滤的规则，则这个过滤器的误判率也会上升，有可能将正常邮件错
误判断为垃圾邮件。对于大多数用户来说，错过一封正常邮件的后果要比收到
垃圾邮件严重得多，所以一个良好的过滤器是不能误判邮件的，这是一种“宁
可放过，不可杀错”的场景。
在这种情况?，一位名为保罗·格雷厄姆（Paul Graham）的工程师提出
可以使用“朴素贝叶斯”的方式过滤垃圾邮件，并且从他的试验结果来看效果
非常好，它可以过滤掉1000封垃圾邮件中的995封，并且这995封中没有一个误
判。更强大的地方在于这个过滤器能够自我学习，会根据新收到的邮件不断调
整模型，收到的垃圾邮件越多，它的判定效果就越好。
如此神奇的分类器是怎么实现的呢？实际上，格雷厄姆只是建立了一个基
于朴素贝叶斯的分类器。在数据准备阶段，他找到正常邮件与垃圾邮件各4000
封。首先解析所有的邮件，提取这8000封邮件里的每一个单词建立一个词汇
库，这个库包含了两张表，其中一张记录所有在邮件中出现过的词语，另外一
张则对应统计这些词语各自出现的频率。接?来计算每个词在正常邮件与垃圾
邮件中出现的频率。例如我们检测出在4000封垃圾邮件中有200封邮件中包
含“sex”这个单词，则该单词在垃圾邮件中出现的概率是5%。而在4000封正
常邮件中只有2封包含这个词，则该单词在正常邮件中出现的概率为0.05%。有
了这个初步统计结果，分类器就可以投入使用了。
当我们收到一封新邮件时，它只可能是正常邮件或垃圾邮件。因此我们假
定 先 验 概 率 为 50% 。 用 S 表 示 垃 圾 邮 件 （ spam ） ， 用 H 表 示 正 常 邮 件
（healthy），则P(S)和P(H)的先验概率都是50%，如?所示：
P（S）=P（H）=50%
解析这封新邮件，发现包含关键词“sex”，此时这封新邮件是垃圾邮件
的概率是多少呢？
我们用W表示“sex”这个词，问题变成了如何计算P(S|W)的值，即在某个
词语（W）已经存在的条件?，是垃圾邮件（S）的概率有多大。根据条件概率
公式，可得：

 

式中，P(W|S)和P(W|H)表示的是这个词语在垃圾邮件和正常邮件中分别出
现的概率。对“sex”这个词，我们计算出来这两个概率分别为 5%和 0.05%，
且 P(S)和 P(H)的值都等于50%。因此可以计算P(S|W)的值为： 从上述推断过程可以看出来，“sex”这个词具有很好的判定效果，将原
本50%是垃圾邮件的概率一?子提升到 99%。但是现在我们就能直接?结论说
这封新邮件就是垃圾邮件吗？有些正常邮件中可能也会包含“sex”这个单
词，如果单凭一个词去判断，未免过于?断。聪明的格雷厄姆当然也想到这个
问题。它采用的解决方法是选出这封信中P(S|W)最高的15个词，计算它们的联
合概率。
联合概率指的是在多个事件发生的情况?，另一个事件发生的概率有多
大。假定W1和W2都是垃圾邮件中经常出现的词语，如果它们都出现在同一封邮
件里，那么这封邮件是垃圾邮件的概率就称为联合概率。联合概率的计算公式
如?：
P（A 1 A 2 A 3 …A n ）=P（A 1 ）P（A 2 |A 1 ）P（A 3 |A 1 A 2 ）…P（A n |A 1 A 2 A 3
…A n−1 ）
有了这个公式以后，对所有新邮件都可以用它来判定是否为垃圾邮件。在
使用这个公式时，就像使用线性回归进行分类一样，需要设置一个阈值，高于
这个阈值的邮件才会被判定为垃圾邮件。格雷厄姆经过反复测试后，将阈值设
置为0.9，这个时候效果最佳。某封邮件经过联合概率计算后若结果高于0.9，
则表示经过15个词联合认定这封邮件有 90%以上的概率为垃圾邮件。由此，一
封正常的邮件即使包含了某些关键词也不会被认定为垃圾邮件，分类的效率大
大提高。
朴素贝叶斯算法不但能够将普通的垃圾邮件找出来，当发件人尝试改变邮
件的句子结构、词语、显示效果，甚至以“有一款新1产1品”这样的方式来绕
过反邮件系统时，朴素贝叶斯算法也能展示出其独特的优势。因为它是基于统
计的方法，只要新来的邮件中含有以往没出现过的词语，分类器都将自动将
这些词语凸显出来，并根据敏感性给它们分配适当的权重 。这样无论遇到什
么样的新组合词语，都?不出贝叶斯分类器的筛选。

6.3.2 朴素贝叶斯的实现过程
从上述的案例可以看出来，朴素贝叶斯算法的实现方式与其他的机器学习
算法基本相同，如图6-6所示，主要分为三个阶段。

 

 （1）准备工作阶段：这个阶段的任务是为分类做必要的数据准备。朴素
贝叶斯分类属于有监督学习，建模前需要准备大量正确样本以及错误样本，且
样本属性的取值只能是布尔型或数值型数据。我们拿到的样本的有些特征可能
是连续型变量，例如人的身高、体重或物体的长度等，这些特征可以通过分段
的方式转换成离散值。例如将“身高”划分为170cm以?的区间，特征值用1表
示；170cm到180cm的区间，特征值用2表示；180cm以上的区间，特征值用3表
示。
选择过多的特征对朴素贝叶斯算法来说并非好事。在选择特征的时候，我
们可以绘制一个特征直方图来帮助我们挑选出合适的特征，并对每个特征进行
适当划分，人工挑选一部分待分类项进行分类，形成训练样本集合。这一阶段
的输入是所有待分类样本，输出是特征和训练样本。
这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，特征的质量
对整个建模工作有重要的影响，分类器的效果在很大程度上由特征、特征划分
方式及训练样本质量决定。
（2）分类器训练阶段：这个阶段的任务是生成分类器。主要工作是计算
每个类别在训练样本中的出现频率及每个特征在所有划分?的条件概率，并记
录结果。这一阶段的输入是特征和训练样本，输出是分类器。我们可以用准确
率、误判率等指标指导模型校准，提升模型分类效果。
（3）应用阶段：这个阶段的任务是使用分类器对待分类项进行分类。其
输入是分类器和待预测样本。计算每个类别的后验概率，最后提取后验概率最
高的15个特征组成联合概率，判断联合概率是否高于现有的阈值，以实现样本
的分类。
6.4 进一步的提升
6.4.1 词袋子困境
实现需求以后，我们不能仅满足于解决现有问题。作为产品经理当然还要
去思考这个解决方案有没有进一步提升的空间，这个过程中还有什么细节目前
做得不够好，我们可以想办法优化。
现在我们知道，朴素贝叶斯实际上就是增加了条件独立假设作为前提的贝
叶斯算法。正是这样一个假设大大简化了贝叶斯算法的计算方式，同时我们也
能在现实生活中找到文本信息处理这一匹配假设的场景。任何事物都存在两面
性，虽然这样做在文本处理领域可以解决不少问题，但同样也会遇到新的问
题。
我们仔细思考后会发现，因为朴素贝叶斯假设所有的词语之间都没有关
联，所以缺少对词语的组合顺序的理解。在这种情况?，如果一封邮件只
有“请基金产品经理看看”这句话，那么在计算联合概率时你会发现，“请基
金产品经理看看”与“经理请看看基金产品”这两句话的联合概率是相同的，
而后者可能在一些广告邮件中出现。这就相当于朴素贝叶斯分类把所有的词汇
扔进一个袋子里随便搅和，认为它们无论怎么组合表达的意思是一样的，因此
这种情况也称作词袋子模型。
然而，邮件中的每个词都不重复，这在现实中其实非常少见，尤其是在一
封垃圾邮件里。如果文本的长度较长，必然会有许多词语重复出现，比如一封
邮件的内容为：“2019 新春爆款产品上市，多款产品适合不同需求的你，快
来挑选心仪的产品吧。”这封典型的垃圾邮件中仅“产品”一词就重复了三
遍。但在词袋子模型里，无论一个词语重复了多少遍，对整体概率的计算都没
有多大的影响，并不会因为某个词多次重复就对它重点关照，这显然是不
够“智能”的。根据生活经验我们知道，通常垃圾邮件为了突出某些内容，肯
定会大量重复某个词语或固定的句式，因此在这个地方我们可以采取一些措施
提升模型的辨别能力。
6.4.2 多项式模型与伯努利模型
对于这个问题，目前常用的解决方法是采用多项式模型、伯努利模型或两
个模型相结合的混合模型。为了搞清楚这两个模型的区别，首先我们要知道文
本是如何分类的。
假设现在有一封邮件的内容为：“新品上市欢迎咨询。”我们可以用一个
文本特征向量来表示这封邮件的内容，即x=(新，品，上，市，欢，迎，咨，
询)。在邮件分类中，我们需要给这封邮件打上一个标签，假设把邮件x归类
到“垃圾邮件”中，即打上“垃圾邮件”的标签，用c表示。
伯努利模型也称为文档模型，在模型中以“文档”为统计单位，统计某个
特征词出现在多少个文档中。假设某个特征词只在某一个文档中出现多次，贝
努利模型在统计的时候会忽略该词出现的次数，只算作一次。因此在伯努利模
型中，每个特征的取值范围为{0,1}，0代表没有出现，1代表出现过。在邮件
分类中，就是指一个特征有没有在邮件中出现过。
而多项式模型也称为词频模型，即以“词”为统计单位，当某个特征词在
某个文档中多次出现的时候，与伯努利模型相反，它算作多次。如果总共用
8000封邮件构成词汇库，其中恰好在一封垃圾邮件中“水杯”一词出现了1000
次，则往后当遇到一封新的正常邮件时，只要其中出现了“水杯”一词就很可
能被分为垃圾邮件。
两个模型最大的区别在于两者的计算粒度不一样，多项式模型以单词为粒
度，伯努利模型以文档为粒度，因此二者的先验概率和条件概率的计算方法都
不同。当计算后验概率时，在多项式模型中，只有在邮件中出现过的单词才会
参与后验概率的计算；但是在伯努利模型中，某个单词即使没有在邮件中出
现，只要在词汇库中存在，最后也会参与计算。在进行模型计算时，这种在词
汇库中出现但是在邮件当中没有出现的单词会被当作“反方”，作为一个惩罚
项参与。从两个模型的特性上看，伯努利模型更适合处理短文档，在词汇数
量较少时效果较好；而多项式模型适合处理长文档 ，在词汇数量较多时效果
比较好 。
朴素贝叶斯算法还存在另外一个问题，就是对数据稀疏现象过于敏感。假
设在一封邮件中出现了一个词汇库中不存在的单词，按照朴素贝叶斯模型的计
算方式，会认为这个词在任何一封邮件中出现的概率都为0，所以最后计算联
合概率时结果也为0。这样得到的结果并不合理，因为我们不能因为在某封邮
件中有一个单词从来没有出现过，就判断这封邮件百分之百不是垃圾邮件。
为了解决零概率的问题，法国数学家拉普拉斯最早提出用“加1”的方法
估计没有出现过的单词的概率，所以加法平滑也叫拉普拉斯平滑，是比较常用
的平滑方法。它的解决思路非常简单，就是对每个类别?所有划分的计
数“+1”，这种方式并不会对结果产生影响，并且解决了上述联合概率为零的
问题。很多时候简单的方式恰恰也是最有效的方式，就是这样一个简单的调
整，问题迎刃而解。
解决了词袋子困境以及数据稀疏问题以后，实际上我们已经获得了一个效
果非常好的垃圾邮件分类器。由此可以看出，朴素贝叶斯算法本身就具备非常
高效、简单的解决思路，只需进行一些小的改进，就能够解决不少问题。