论文阅读 Adaptive Consistency Regularization for Semi-Supervised Transfer Learning

Adaptive Consistency Regularization for Semi-Supervised Transfer Learning

论文题目：自适应一致性正则化方法用于半监督迁移学习
作者单位：百度大数据研究院
作者：Abulikemu Abuduweili
代码地址：https://github.com/SHI-Labs/Semi-Supervised-Transfer-Learning

摘要

近来，半监督学习模型在处理带标签数据不全的任务中有着优异的表现。但它们的参数都是随机初始化的。而本文是结合了迁移学习和半监督学习，即利用预训练模型和半监督所用的标记/未标记的数据达到更好的效果。如何结合二者，本文引入了自适应一致性正则化方法。它由两个互补的组件组成：源模型和目标模型之间的自适应一致性，有标签和无标签数据支架的自适应一致性。一致性正则化的例子是根据它们对目标任务的潜在贡献进行自适应的选择。
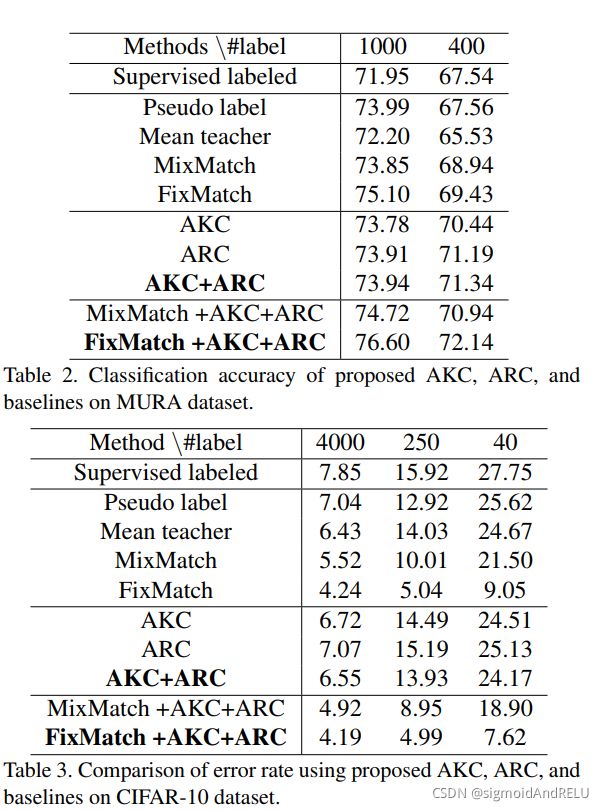
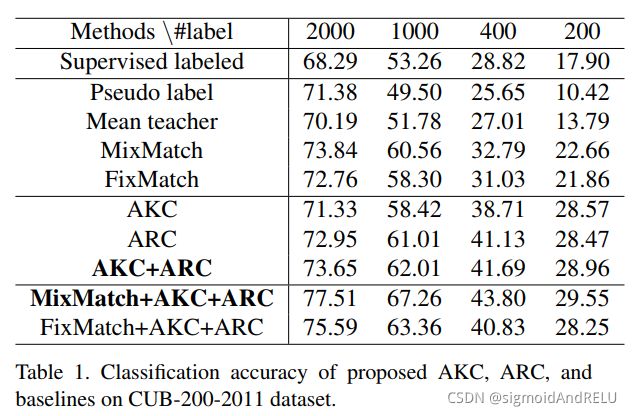
现有的最先进的半监督方法：伪标签，Mean Teacher，Fix Match（固定匹配）.
实验数据集： CIFAR-10, CUB-200, and MURA。

小结：本文提出了结合 半监督+迁移 两种方法的思想，并设计了一个自适应一致性正则化方法来加以实现。所以懂得这几个方面的知识就算合格了。

引言：
半监督学习的优点比比皆是，当然对比对象是监督学习，能够更好的利用带标签和无标签的数据，具有更广泛的应用性。现有的SOTA方法主要有三类：基于正则化方法的一致性、熵最小化、伪标签。
本文从大规模数据集的一般目的性出发来考虑，就像ImageNet和Places 365。
而迁移学习的强大在于，在这些庞大数据集训练过后，在别的应用场景下依然有着非常好的泛化能力。

在说完这两个方法的优点后，本文得着重提一句：半监督学习对于预训练模型的微调作用可能不明显，但没有人系统的研究这个问题。是的，本文就来研究研究！

所以本文的贡献如下：
1、首次提出半监督迁移学习深度神经网络框架。
2、引入了自适应一致性正则化方法。
3、实验结果优于经典的半监督学习方法，并且能够对fixMatch和MixMatch有额外的提升。

相关工作

深度迁移学习

先前研究分为：归纳迁移、转换迁移、无监督迁移。是根据源域和目标域之间的关系和样本是否带标签来分的。而在深度学习领域中，基本就是以下三种。

微调

通过简单训练来达预训练模型对目标任务的认识，或者是通过注意力图来完成迁移学习的关注度，从而提高迁移学习的效率。

域自适应

这是为了处理训练数据同测试数据的样本选择偏差问题，对于一些早期的研究，样本重加权算法来调整通过训练实例学习到的决策边界，以适应目标域。另一个有用的想法是显式地最小化源域和目标域之间的分布距离。算通过样本重加权和表征适应等方法学习适当的特性转换，可以同时将两个域投影到共享表示空间中。
测试域和训练域之间的相似度越高，那么模型的训练得到的效果越好。

few-shot learning

这是一种利用人类的学习能力设计出来的学习方法。在已有的经验上，人能够快速的提取到一个物体的可辨识特征信息，并由此对物体有着清晰的认识度。
最近的研究设计了一个TransMatch的模型，由MixMatch和Imprinting技术结合的框架，能够有这种半监督 的few-shoting学习能力。

半监督学习

基于一致性的正则化，熵最小化，和伪标签。所有这些方法都有一种利用用额外的未标记数据来探索潜在结构的欲望。这也是我们想要辨认的标签所指示的样本分离。而本文中只讨论了基于一致性正则化的分支。

一致性正则化

一致性正则化是决策边界不太可能通过高密度区域和一个样本和它的近邻被期望具有相同的标签这样的想法形成的。许多自监督的学习方法都关心未标记数据的利用。
有以下几种方法：
使用不同噪声对输入样本进行增强，并且添加正则化项来减少输出相对于原始输入的扰动对等点之间的差异。
Mean Teacher 和Temporal Ensembling 是集成学习使用移动平均全职或预测来提高干扰样本的质量的方案。
近来，ICT插值一致性训练使用未标记样本添加随机噪声改进了扰动方法，在处理低边际未标记点时，这被认为是一种更有效的转换。MixMatch进一步提出了对未标记数据的人工标记锐化，并在Mixup中混合标记和未标记数据，FixMatch延续了结合不同机制来开发未标记的例子的趋势。

本文的工作并没有寻求在迁移学习设置中，在那些一般的半监督学习算法中寻找最佳的选择

半监督迁移

半监督迁移学习可以看作是常规半监督学习的自然扩展，考虑相关的辅助任务，或者作为常规迁移学习的一部分标记目标实例的扩展。
主要是前人没有这方面的研究，早期的工作重点是使用传统的机器学习框架，他们提出了一种改进的归纳迁移学习共训练方法，并根据训练误差进行实例重加权。对两个具有不同k值的不同的k最近邻(kNN)学习者进行协同训练。最近，[55]提出了一项实证研究，表明当我们从预先训练的模型开始调整目标任务时，与完全监督的基线相比，最先进的SSL技术的收益减少，有时甚至消失。虽然这些观察结果指出了考虑这一更具竞争力和实践基准的必要性，但它们并不是为了发明一个解决方案。

框架

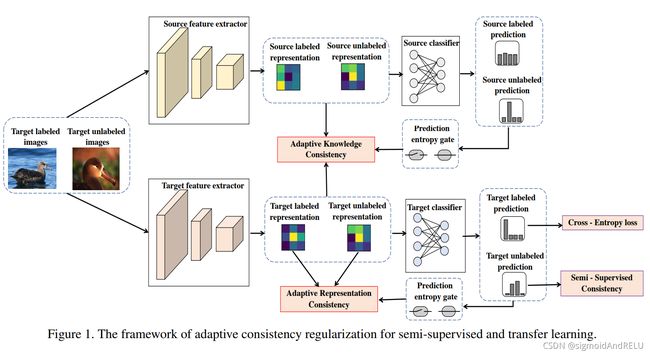
本文的重点在此，流程如下：
将带标签的和无标签的图像输入到源特征提取器和目标特征提取器中，分别得到标签的特征图，然后一部分经过AKC模块，（Adaptive Knowledge Consistency，一个正则化块。），另一部分经过特定的分类器得到相应的预测结果，并且不同的特征提取器对应不同路线的输出，使用正则化模块来对模型的特征提取进行微调。对于源特征提取器，使用交叉熵门控来调控，而对于目标特征提取器，使用半监督的一致性损失和交叉熵损失来共同调控，当然，交叉熵对应有标签的数据而一致性则针对无标签数据。
重中之重 ACK

Adaptive Knowledge Consistency

自适应一致性正则化，这里涉及到知识蒸馏的一部分知识就不赘述，虽然与以往的研究不同，但我们同时使用标记数据和未标记数据作为知识转移的桥梁，并施加自适应样本的重要性，以防止两个数据集之间的差异导致的负转移。
本文使用KL散度或均方误差，来衡量预训练特征提取器和目标特征提取器在数据集上的相似度差异。
在我们的设置中，定义$L={x_l^i}^{B_l}\in D_t^l$
R的表达式可归于一下：
$R_K=\frac{1}{B_l+Bu}{\sum }_x^i\in L\cup U{w}_K^{i}KL(F_{\theta o},F_{\theta }(x^i))$
在计算样本重要性参数$w_K^i$时，本文将预训练模型的参数${\theta }^o$和${\phi }^o$取平均。
$w_K^i=G(H(P_s^i))=G(-{\sum }_{j=1}^{C_s}{P}_{s,j}^{i}log(P_{s,j}^i))$
其中X是输入张量，得到最后的分类结果使用熵计算样本x的权重。
G是熵门控，并设计了一个阈值判定式来限制w的取值。
$w_K^i=I(H(P_s^i)<={ǫ}_K)$

Adaptive Representation Consistency

本文引入了另一个强制性正则化器，自适应分布一致性。为了解决过拟合问题。因为无标签的样本中也有数据结构的信息，将这些无标签的样本整合起来能够提高模型的泛化能力。所以，本文使用经典的矩阵最大化平均差异（MMD，(求不同样本在function熵的函数值的均值，就可以得到两个分布之间的差异值，function一般取高斯核函数（RBF）):
$MMD(Q_v,Q_u)=||\frac{1}{m}{\sum }_{i=1}^{m}k(v^i)-\frac{1}{n}{\sum }_{j=1}^{n}k(u^j)|{|}^2$
k是核函数。
使用MMd方法能够对有标签数据和无标签数据的分布进行判断。
而这个限制依旧存在着个严重问题：目标模型是逐步学习得来的，所以在训练的早期，无标签数据的多少并不能影响数据表示的分布准确性。
为了克服这个问题，本文使用样本采样方法，并计算熵的softmax值，只有置信度达标的样本才能参与模型的训练。

模型的总结
本文就是将两种思想融合起来，并使用具体的方法来解决相应的问题，AKC也好，ARC也好，都是具体的方法。精髓已得，下面看实验结果便是。

实验结果

实验量是一篇论文的核心，所以在阅读论文的过程中要体会到实验都重要性，CVPR的论文对此要求更是严格，所以请读者们注意到这个问题！

有收获就支持一下作者吧！~~