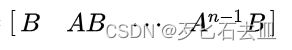汽车悬挂系统的现代控制分析（现代控制理论课程小论文）

目录

• 0.摘要 4
  1. 建立模型 5
  1.1. 物理系统分析 5
  1.2. 数学模型 5
  1.3. 计算机仿真 8
  2. 能控能观性判别 10
  2.1. 能控能观性定义 10
  2.2. 判别方法 10
  2.3. 进行判别 11
  3. 稳定性分析 12
  3.1. 稳定性定义 12
  3.2. 判断稳定性 12
  4. 状态反馈控制器设计 12
  4.1. 控制器定义 12
  4.2. 控制器设计分析 13
  4.3. 控制器系统仿真 15
  5. 状态观测器设计 17
  5.1. 观测器的定义 17
  5.2. 观测器设计分析 18
  5.3. 基于观测器的控制系统仿真 19
  6. 最优控制设计 24
  6.1. LQR最优控制 24
  6.2. 最优控制设计 25
  6.3. 最优控制仿真 27
  7. 总结 28
  8. 参考文献 28
  9. 代码附录 29

摘要

随着社会的进步、科技的发展，人们生活水平不断提高，乘坐车辆的频率增多，对于汽车乘坐舒适性的要求也越来越高。另一方面，由于最近几年国内外汽车制造业的迅猛发展，汽车制造业的竞争也日益激烈，各个汽车制造公司加强研发力量，试图开发出乘坐舒适性好、高性能、经济的产品，以期望使自己公司在激烈的市场竞争中长盛不衰。
理想的悬挂系统不仅能使车随路面起伏而上下运动，并能借此使整个车身在前进过程中尽量保持水平，而且还能随车速、路况、运动方式的变化做出适当、灵敏的反应；同时，它还能使轮胎与路面随时贴合，并使车轮保持适当的角度，从而使汽车的动力性能、制动性能以及转向性能得以充分体现。因此，现代汽车的悬挂系统越来越受到业内人士的重视。
为了使乘客乘坐舒适，有必要对汽车的悬挂系统的振动性能进行深入分析。需要透彻地分析汽车悬挂系统的动力特性，从而剖析车辆行驶的运动特性。分析汽车悬挂系统是改进车辆的运动特性的依据，是提高汽车行驶中的舒适性与安全性的基础。
本文立足于现代控制理论，着重分析了汽车悬挂系统的数学模型，并进行了系统仿真，对其减震、抗震性能进行分析。本文聚焦于汽车进行减震的现代控制方法，并对其中暴露出来的一些现象进行剖析以及规律性探索和总结。
关键词：现代控制、悬挂系统、减震、状态反馈控制、状态观测器、LQR

1.建立模型

汽车悬挂是连接车轮与车身的机构，对车身起支撑和减振的作用。主要是传递作用在车轮和车架之间的力，并且缓冲由不平路面传给车架或车身的冲击力，衰减由此引起的震动，以保证汽车能平顺地行驶。

1.1.物理系统分析

为了便于建模，将车辆简化为车体、车架、弹簧、阻尼四部分组成，如下图所示。控制器V安装在悬挂系统与车体之间，另一个输入W是凹凸不同的地面带来的，W是不受控制的，更像是一种噪音。W和V共同构成了系统的二维输入u。

系统物理模型

1.2.数学模型

系统（A，B，C，D）建立如下：

其特征根为：

均具有负实部，所以系统是稳定的，但是特征根距离Y轴比较近，所以系统收敛比较慢。存在共轭的部分，所以会产生震荡。

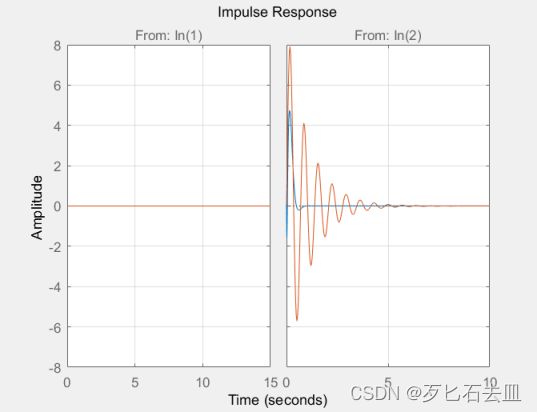
原系统的冲激响应和阶跃响应

1.3.计算机仿真

对系统不加控制（v=0）的进行仿真,以验证系统的一些性能。

原系统的仿真

原系统的阶跃响应

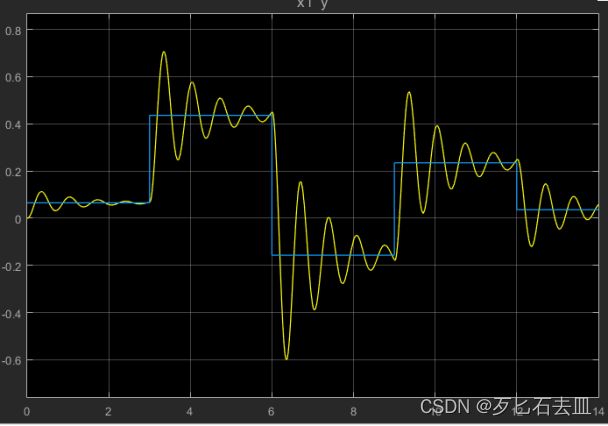
原系统的多段响应
从原系统的阶跃响应可以看出，如果对于悬挂系统不加控制，可能舒适度就会非常差，这是对于日益现代化的时代来说是不能接受的，因此要设计控制器进行校正。

2.能控能观性判别

2.1.能控能观性定义

能控性是指状态空间方程能否能通过改变输入来控制。 能观性是指是否能通过输出来观察系统的初始状态。 系统内部每个状态变量都可以由输入完全影响,则称系统状态为完全能控。 系统内部每个状态变量都可以由输出完全反映,则称系统状态为完全能观测。能观测性属于表征系统状态运动可以由输出完全反映的一种定性属性。

2.2.判别方法

为了编程方便，选取能控能观性的直接判别的方法。
能控性：

只要能控性矩阵为满秩矩阵，则系统能控。
能观性：

只要能观性矩阵为满秩矩阵，则系统能观。

2.3.进行判别

针对汽车悬挂系统它的能控能观性矩阵计算如下。

因为能控性矩阵和能观性矩阵的秩均为4，与系统维数一样，所以系统能观能控。

3.稳定性分析

3.1.稳定性定义

对于一个LTI系统，其严格稳定的充分必要条件是：对于任意对称正定矩阵Q，Lyapunov方程都有一个唯一解矩阵P是对称正定的。因此，研究给定线性系统的一个有效的方法是从一个给定的正定矩阵Q中，推出正定矩阵P。其一般步骤是：
1.选择一个正定矩阵Q，一般选择单位阵I
2.从下面的Lyapunov方程中解出矩阵P

3.检验P是否是正定矩阵。如果P是正定的，那么就是这个线性系统的一个Lyapunov方程。并能够保证其全局渐进稳定性。

3.2.判断稳定性

选取Q矩阵为单位矩阵，解出P矩阵为：

P矩阵各阶代数余子式的行列式不为零，则P矩阵正定，那么系统具有全局渐进稳定性。

4.状态反馈控制器设计

4.1.控制器定义

系统控制率表达为：

如果系统特征方程的根都位于s平面左半平面，则系统稳定
因此，给定A和B后，只要系统完全能控，一定可以找到合适的矩阵K使得系统的极点配置在s左半平面的任意位置。
可以先设出K值，之后带去进行计算。然后与期望的特征多项式比对，得出K的值。

4.2.控制器设计分析

上一章得出一个重要的前提条件，系统所有状态变量都可以直接观测（系统可观），同时系统也是可控的。

然后就可以得到新的A，记为A0。
新的系统（A0，B，C，D），表达为：

验证极点配置后的系统的性能：
如图，蓝线这是新系统的阶跃响应，对比旧系统的橙色的线有很大的改观，各种参数由来一定的提高。

加控制器之后阶跃响应比较

4.3.控制器系统仿真

进行状态反馈控制，输入v，变为是关于状态变量的函数，且具有不同的系数。将这些系数带入仿真中就可以对控制效果进行仿真。

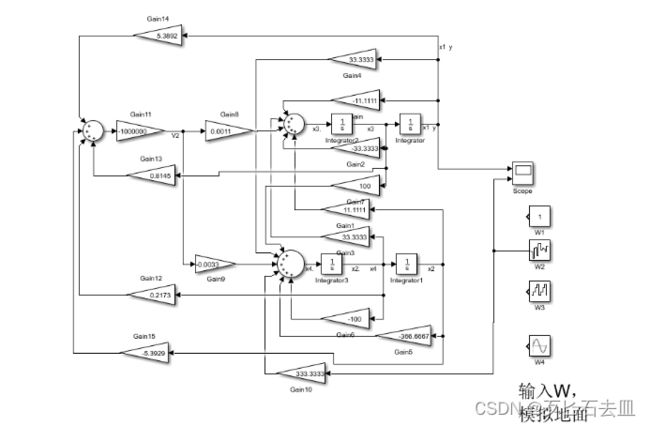
加控制器后的计算机仿真
下图是系统的阶跃响应和，它对凹凸不平地面的响应。可见其可以快速的追踪地面的变化，且反应可以发出舒缓，几乎没有抖动和上下起伏。

加控制器后的阶跃响应仿真

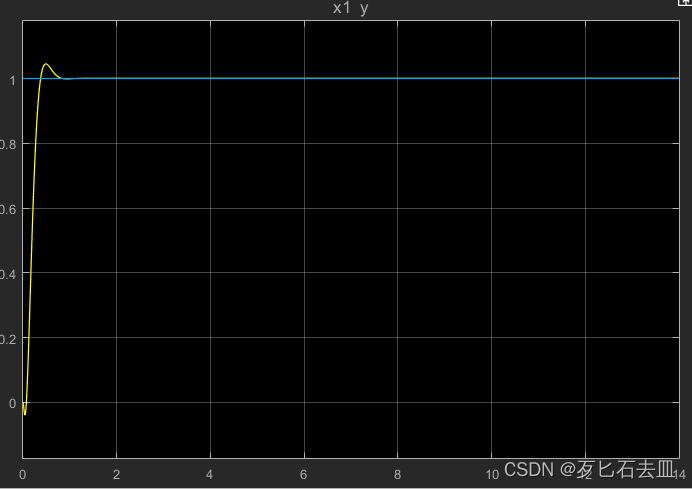
加控制器后的多段阶跃响应仿真

5.状态观测器设计

5.1.观测器的定义

到目前为止，对于状态反馈控制器设计方法都是基于状态变量全是已知的。然而在很多情况下，这是不可能抑或是技术上有很大难度。那么对于那些未知的状态变量，如何才能借助仅有的可测的输出变量以及已知的输入变量来求得？这就是状态观测器的思想的由来。现在依然基于线性时不变的MIMO系统来设计状态观测器。

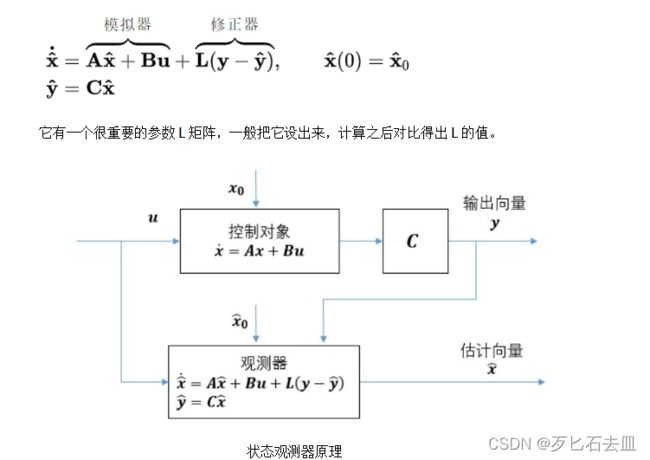
设计观测器的特征值时，为了尽快让模拟器的状态估计值逼近实际值，而不再有观测估计误差，应该尽可能让观测器的特征值的实部绝对值设计的大一点，至少误差衰减速度要比系统动态矩阵的主导特征值要更快。
需要明晰的是——状态观测器解决的不是数学模型能不能输出状态的问题，而是你的数学模型输出的状态值跟被控对象的实际状态值是否一致的问题。

5.2.观测器设计分析

这里设计状态观测器的四个特征值全为-50。
利用acker（）函数计算出期望观测器对应的L值：
L：

估计的状态变量与实际的状态变量进行比对得出下图。可见在初始0.2s内，估计值于实际值出现较大偏差，但是0.5s之后这个偏差就变为0。可见观测器的效果还是十分优良的。

4个状态变量的估计误差

5.3.基于观测器的控制系统仿真

基于观测器的状态反馈控制系统
基于状态观测器的控制系统的控制效果如下图所示，与直接进行状态反馈进行控制的效果相差无几。

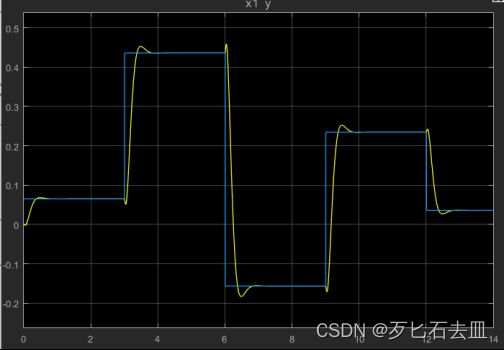
多段阶跃输入的追踪效果
由于状态观测器对于系统状态变量的观测效果非常好，以至于在图中无法分辨状态变量和估计的状态变量。因此赋予估计的状态变量x1一个非零的初值1。这样就可以分不出状态估计与原状态变量的区别。下图是给予非零初值后的控制效果，可见刚开始控制还是出现较大的波动，但随后就可以达到较优的效果。可见系统具有一定的鲁棒性，可以应对一定程度的干扰。

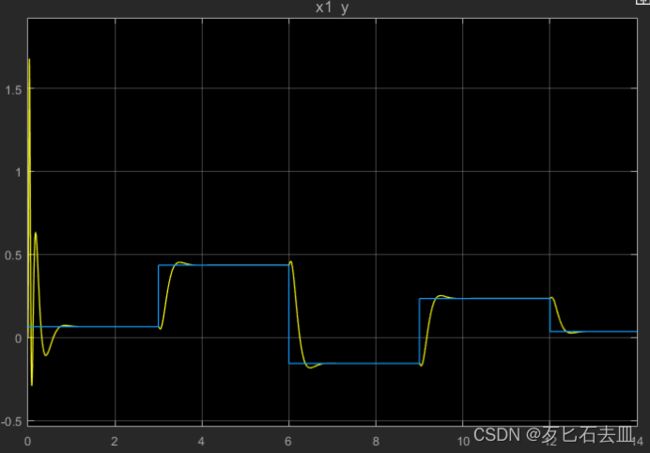
引入初始偏差的多段阶跃输入的追踪效果
下图是状态变量x1与状态变量x1的估计值变化规律，可见一段时间后两者几乎重合，估计效果较好。

状态变量x1与状态变量x1的估计值
下图是状态变量x2与状态变量x2的估计值变化规律，可见一段时间后两者几乎重合，估计效果较好。

状态变量x2与状态变量x2的估计值
下图是状态变量x3与状态变量x3的估计值变化规律，可见一段时间后两者几乎重合，估计效果较好。

状态变量x3与状态变量x3的估计值
下图是状态变量x4与状态变量x4的估计值变化规律，可见一段时间后两者几乎重合，估计效果较好。

状态变量x4与状态变量x4的估计值

6.最优控制设计

6.1.LQR最优控制

通过特征值或是极点的预置，可以让反馈增益很明确地算出来，然后再让闭环系统实现期望的动态。
然而实际设计时，会有很多实际技术条件限制，因为对特征值的配置实际上对单个状态变量或是输入控制量的反馈控制行为没有直接的影响。为了平衡各种限制以及设计要求，我们需要另寻设计准则，线性系统最优控制就是这样一个考虑了控制量大小的设计思路[1]。
LQR相比于极点配置更具有优势，因此它本质利用代价函数（类似于MPC）来找到一个可以同时考虑性能和最少的输入能量（以最小的输入值来满足控制需求）的一个最优解，LQR一般形式表示如下：

在系统中，矩阵P是关于矩阵K的一个矩阵，也是唯一可以改变的矩阵，因此求代价函数J极值问题转换为J导数的极小值问题,因此可以通过下式获取矩阵K，进而获取了代价函数的最小值，也就是系统的最优解。
LQR最优控制是状态反馈的一种控制方法，控制结构和极点配置的状态反馈一致，仅是在获取矩阵K的角度上不同，基于极点配置的状态反馈控制强调获取系统极点的位置，通过位置来判断性能。LQR最优控制强调在完整的时域内得到最优的动态性能（即系统状态变量趋近于平衡点的平均速度最快），其次LQR最优控制可以通过代价函数来同时控制多目标性能的变量，进而满足不同系统的需求特点。

6.2.最优控制设计

现在的系统（A，B，C，D），表示如下：

原系统的阶跃响应（红线）与经过最优控制的系统（蓝线）有很大的差别。最优控制可以达到改善系统性能的目的，效果较好。

原系统与经过最优控制的系统的阶跃响应

6.3.最优控制仿真

将最优控制LQR得出的K值带入仿真里面，可以验证最优控制的效果。

最优控制系统的计算机仿真
最优控制之后的系统可以控制系统，且控制效果相比原系统来说有了很大的提升。但是，没有比得上直接进行极点的控制方法。

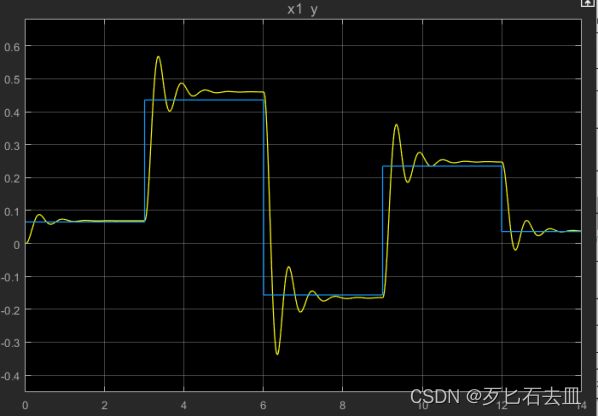
最优控制系统多段阶跃响应

7.总结

不加控制的汽车悬挂系统是一个性能比较差的系统，但整体是稳定的，也是可观测可控制的。因此可以对其进行状态反馈控制和状态观测器的设计，以及可以实现基于状态观测器的状态反馈控制，并且对于它们分别进行MATLAB仿真，都得到了不错的效果，可以很好的达到目标。最后，使用LQR最优控制，性能明显优于原系统，但没有超过极点配置的控制器的控制效果。

8.参考文献

[1]Regelungstechnik B (Zustandsraummethoden) (WS 2019), Prof. Dr.-Ing. Knut Graichen Lehrstuhl für Regelungstechnik, Friedrich-Alexander-Universität Erlangen-Nürnberg

9.代码附录

%%
clc;clear
%%
%----------------变量赋值----------------
m1=900;m2=300;k2=10000;c=30000;k1=10*k2;
%----------------ABCD矩阵----------------
A=[0      0      1      0;
   0      0      0      1;
  -k2/m1 k2/m1 -c/m1 c/m1;
  k2/m2 -(k2+k1)/m2 c/m2 -c/m2];
B=[0 0;0 0;1/m1 0;-1/m2 k1/m2];
C=[1 0 0 0];
D=[0 0];
%----------------模型建立---------------
G=ss(A,B,C,D)
[num,den]=ss2tf(A,B,C,D,1)  %将状态空间表示形式转换为传递函数
tfsys=tf(num,den)
eig(A)  %求特征值
subplot(211)
impulse(G)
subplot(212)
step(G)
%% 能控能观性判别
N=size(A);
n=N(1)
CM=ctrb(A,B) %能控性矩阵 controllability matrix
OM=obsv(A,C) %能观性矩阵 observability matrix
cm=rank(CM)
om=rank(OM)
if (cm==N&&om==N)
    disp('此系统能观能控')
end
%%  稳定性判别
Q=eye(4,4);
P=lyap(A',Q);
if(det(P(1:1,1:1))>0&&det(P(1:2,1:2))>0&&det(P(1:3,1:3))>0&&det(P(1:4,1:4))>0)
    disp('稳定');
else
    disp('不稳定');
end
%% 状态反馈控制器
HPole=[-200 -100 -7.07+sqrt(-50) -7.07-sqrt(-50)];
K=acker(A,B*[1 0]',HPole)
A0=A-B*[1 0]'*K;
eig(A0)
NG=ss(A0,B,C,D)
figure(1)
impulse(NG)
hold on
impulse(G)
axis([0,10,-4,4]);
grid on
%% 状态观测器
op=[-50 -50 -50 -50];
L=(acker(A',C',op))';
A1=[A -B*[1;0]*K;L*C A-L*C-B*[1;0]*K];
E0=[1 2 0.1 -0.1 0 0 0 0];
t=0:0.01:4;
sys=ss(A1,eye(8),eye(8),eye(8));
[y,t,e]=initial(sys,E0,t);
subplot(221)
plot(t,e(:,1))
grid
xlabel('time')
ylabel('E1');
subplot(222)
plot(t,e(:,2))
grid
xlabel('time')
ylabel('E2');
subplot(223)
plot(t,e(:,3))
grid
xlabel('time')
ylabel('E3');
subplot(224)
plot(t,e(:,4))
grid
xlabel('time')
ylabel('E4');
%% 最优控制
Q=[100000000 0 0 0;0 1 0 0;0 0 100 0;0 0 0 1];
R=0.001;
K1=lqr(A,B*[1;0],Q,R)

源码原文档带价来私聊