【论文阅读】2021-(Pidinet)Pixel Difference Networks for Efficient Edge Detection

---

参考文献： Su, Z., Liu, W., Yu, Z., Hu, D., Liao, Q., Tian, Q., ... & Liu, L. (2021). Pixel Difference Networks for Efficient Edge Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 5117-5127).

文章链接：
https://openaccess.thecvf.com/content/ICCV2021/papers/Su_Pixel_Difference_Networks_for_Efficient_Edge_Detection_ICCV_2021_paper.pdf

摘要

motivations:
基于CNN的边缘检测的高性能是通过一个大的预训练CNN主干来实现的，该主干占用大量内存和能量。传统边缘检测器（如Canny、Sobel和LBP）很少被研究。
contributions:
提出了一种简单、轻量级但有效的架构，称为像素差分网络（PiDiNet），用于有效的边缘检测。PiDiNet采用了新颖的像素差卷积，将传统的边缘检测算子集成到现代CNN中流行的卷积运算中，以增强任务性能。
experiments:
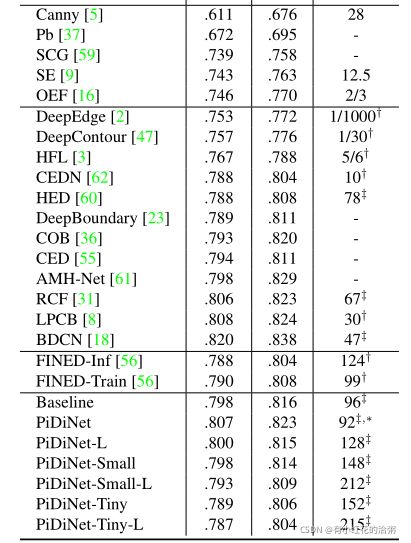
在BSDS500、NYUD和Multicue上进行了大量的实验，以证明其有效性、高训练和推理效率。当仅使用BSDS500和VOC数据集从头开始训练时，PiDiNet可以超过BSDS500数据集上记录的人类感知结果（在ODS F-measure中为0.807 vs 0.803），速度为100 FPS，参数小于1M。参数小于0.1M的更快版本的PiDiNet仍然可以以200 FPS的速度实现相当的性能。NYUD和Multicue数据集的结果显示了类似的观察结果。

1. Introduction

直观地说，边缘表现出不同的特定模式，如直线、拐角和“X”连接。一方面，传统的边缘算子受到这些直觉的启发（下图）。基于梯度计算通过显式计算像素差来编码用于边缘检测的重要梯度信息。然而，这些手工制作的边缘算子或基于学习的边缘检测算法由于其浅层结构通常不够强大。
另一方面，CNN可以学习丰富的分层图像表示，其中普通CNN内核用作探测局部图像模式。然而，CNN核是从随机初始化的，它没有对梯度信息进行显式编码，这使得它们很难聚焦于边缘相关的特征。

基于CNN的实现边缘检测的缺点还包括：
模型尺寸大、内存消耗大、计算成本高、运行效率低、吞吐量低、标签效率低，需要对大规模数据集进行模型预训练。

设计了一种新的卷积运算，以满足以下需要。首先，它可以很容易地捕获图像梯度信息，便于边缘检测，并且CNN模型可以更专注于处理大量不相关的图像特征。其次，深层CNN强大的学习能力仍然可以保留，以提取语义上有意义的表示，从而实现鲁棒和准确的边缘检测。在本文中，我们提出了像素差卷积（PDC），首先计算图像中的像素差，然后与核权重卷积以生成输出特征（见图3）。PDC效果如下图所示：

2. Pixel Difference Convolution（PDC）

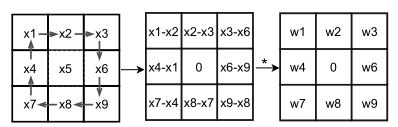
像素差分卷积与普通的vanilla卷积的区别仅在于前者对像素对的差值做卷积，而后者对单个像素值做卷积。公式如下所示：

在具体解释PDC之前，需要扯一嘴LBP是什么东西。

LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和D. Harwood 在1994年提出(注意与本文所属一所大学)，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征；
计算方法：
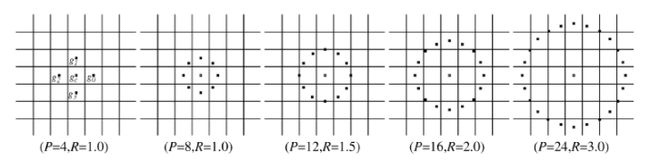
原始的LBP算子定义为在33的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，33邻域内的8个点经比较可产生8位二进制数（通常转换为十进制数即LBP码，共256种），即得到该窗口中心像素点的LBP值，并用这个值来反映该区域的纹理信息。如下图所示：

LBP的相关扩展：将上述LBP的计算范围扩展以解决3×3邻域模板过小，无法捕获大尺度纹理结构的缺点，即下图所示：
①Circle LBP
②LBPROT：在Circle LBP的基础上，解决模板具有旋转不变性的问题。

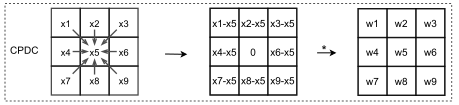
PDC是将上述LBP算法与CNN进行结合，定义了三种PDC的计算方式：central PDC (CPDC), angular PDC(APDC) and radial PDC (RPDC)。如下图所示：

• APDC计算示意图与证明:
  
  
• CPDC计算示意图与证明:
  
  
• RPDC计算示意图与证明:
  

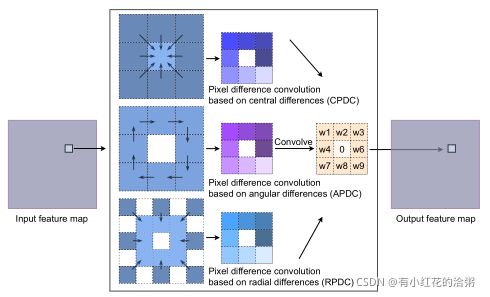
需要注意的是，基于以上公式，一旦模型训练好了，就可以先计算模板权重的差值，再基于权重与像素点进行卷积运算，从而加快推理速度。
这也是这个论文比较大的创新点所在：

在训练阶段运用两倍的算力训练差分卷积的效果，而推理阶段的速度与普通卷积神经网络一致。

3. PiDiNet

网络是作者自己设计的轻量型网络，大量用了可分离卷积，通道注意力结构和并联膨胀卷积提取特征。从头开始训练，没有调用预训练模型。
以及作者后续做了很多消融实验调整模型参数。

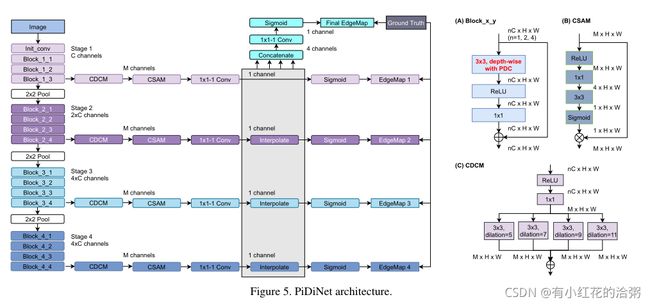
值得提一句这里的损失函数，用的是 annotator-robust loss function，

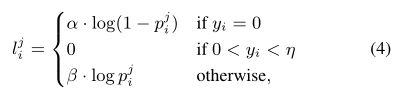
where y i is the ground truth edge probability, η is a predefined threshold, meaning that a pixel is discarded and not considered to be a sample when calculating the loss if it is marked as positive by fewer than η of annotators to avoid confusing, β is the percentage of negative pixel samples and α = λ · (1 − β).

最终损失函数如下：

4. 结果展示

5. 差分卷积代码实现

5.1 CPDC

基于第三节的公式（3），CPDC差分卷积将转为普通卷积相减：

def func(x, weights, bias=None, stride=1, padding=0, dilation=1, groups=1):
    assert dilation in [1, 2], 'dilation for cd_conv should be in 1 or 2'
    assert weights.size(2) == 3 and weights.size(3) == 3, 'kernel size for cd_conv should be 3x3'
    assert padding == dilation, 'padding for cd_conv set wrong'

    weights_c = weights.sum(dim=[2, 3], keepdim=True) #B,C,3,3 -> B,C,1,1
    yc = F.conv2d(x, weights_c, stride=stride, padding=0, groups=groups)
    y = F.conv2d(x, weights, bias, stride=stride, padding=padding, dilation=dilation, groups=groups)
    return y - yc

5.2 APDC

基于第三节的公式（7），APDC差分卷积将转为普通卷积相减：

def func(x, weights, bias=None, stride=1, padding=0, dilation=1, groups=1):
    assert dilation in [1, 2], 'dilation for ad_conv should be in 1 or 2'
    assert weights.size(2) == 3 and weights.size(3) == 3, 'kernel size for ad_conv should be 3x3'
    assert padding == dilation, 'padding for ad_conv set wrong'

    shape = weights.shape
    weights = weights.view(shape[0], shape[1], -1) #B,C,3,3 -> B,C,9
    weights_conv = (weights - weights[:, :, [3, 0, 1, 6, 4, 2, 7, 8, 5]]).view(shape) # clock-wise
    y = F.conv2d(x, weights_conv, bias, stride=stride, padding=padding, dilation=dilation, groups=groups)
    return y

5.3 RPDC

基于第三节的公式（9），APDC差分卷积将转为普通卷积相减：

def func(x, weights, bias=None, stride=1, padding=0, dilation=1, groups=1):
    assert dilation in [1, 2], 'dilation for rd_conv should be in 1 or 2'
    assert weights.size(2) == 3 and weights.size(3) == 3, 'kernel size for rd_conv should be 3x3'
    padding = 2 * dilation

    shape = weights.shape
    if weights.is_cuda:
        buffer = torch.cuda.FloatTensor(shape[0], shape[1], 5 * 5).fill_(0)
    else:
        buffer = torch.zeros(shape[0], shape[1], 5 * 5)
    weights = weights.view(shape[0], shape[1], -1) #B,C,5,5 -> B,C,25
    buffer[:, :, [0, 2, 4, 10, 14, 20, 22, 24]] = weights[:, :, 1:]
    buffer[:, :, [6, 7, 8, 11, 13, 16, 17, 18]] = -weights[:, :, 1:]
    buffer[:, :, 12] = 0
    buffer = buffer.view(shape[0], shape[1], 5, 5)
    y = F.conv2d(x, buffer, bias, stride=stride, padding=padding, dilation=dilation, groups=groups)
    return y