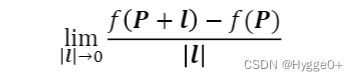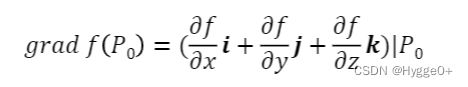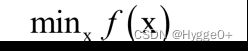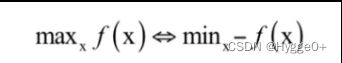机器学习 | 数学基础（一）

【方向导数与梯度】

方向导数是函数定义域内某点P在特定方向l上的导数。

 

梯度是指方向导数取值最大的方向。梯度是一个矢量。梯度指向函数值增加最快的方向。

 

【一点的梯度方向应该如何确定？】

1. 通过导数正负确定梯度方向

【梯度与导数的关系】

梯度是指方向导数取值最大的方向（方向导数为正），则根据方向导数的公式可知梯度指向函数值增大最快的方向。而根据一点邻域内导数的正负可以确定函数值增大还是减小。

【例如】

在一元函数f(x)上，一点的方向导数即为该点在x轴方向上的导数。某点右邻域内导数为负，则表示随自变量增大，函数值减小，即右方向为函数值减小的方向，也就是说这一点的梯度方向指向x轴负方向。

【结论】

可以通过判断某点右邻域内的（偏）导数正负确定该点处的梯度方向。

1. 通过等高线确定梯度方向

梯度方向与等高线切线方向垂直。且指向函数值增大的方向。

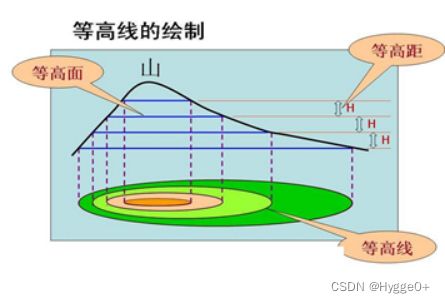
【等高线】

假设我们的损失函数为z=f(x,y)，在几何上表示是一个曲面，该曲面被平面c（c为常数）所截得的曲线l方程为：

Z=f(x,y)

Z=c

这条曲线l在xoy轴面上的投影是一条平面曲线Q，它在xoy平面直角坐标系中的方程为f(x,y)=c，则我们称平面曲线Q为函数z=f(x,y)的等高线。

 

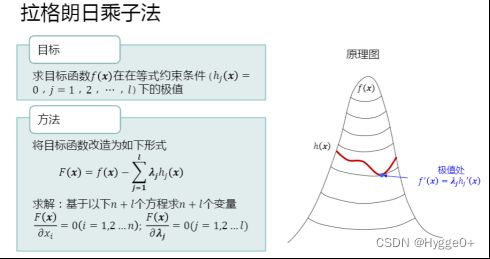
【函数等高线与梯度方向】

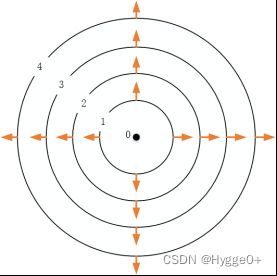
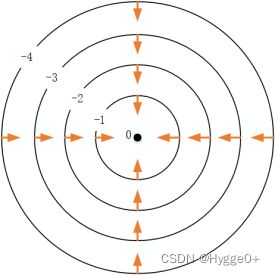
• 凸函数Z = X 2 + Y 2，其梯度为( 2 x , 2 y )。将函数的等高线画出，由内圈到外圈函数值依次增大，梯度指向函数值增加最快的方向（由内指向外侧），故而函数的梯度在x O y 平面内的图像如下：

 

• 函数Z= − ( X 2 + Y 2 )，其梯度为( − 2 x , − 2 y )。同样将函数的等高线画出，由内圈到外圈函数值依次减小，梯度指向函数值增加最快的方向（由外指向内侧），故而函数的梯度在x O y平面内的图像如下：

 

【结论】

形如碗状函数（凸函数，Z=X2+Y2），其梯度方向总是由内侧指向外侧（指向函数值增大的方向）。

形如倒扣碗状函数Z= − ( X 2 + Y2 )，其梯度方向总是由外侧指向内侧（指向函数值增大的方向）。

【凸优化】

【凸函数】任意两点间的函数值小于两点相连线段值

【为什么要特别关注凸函数的优化问题？】

凸函数的特性：凸优化问题中，局部最优解同时也会是全局最优解，使优化问题相对更容易解决。

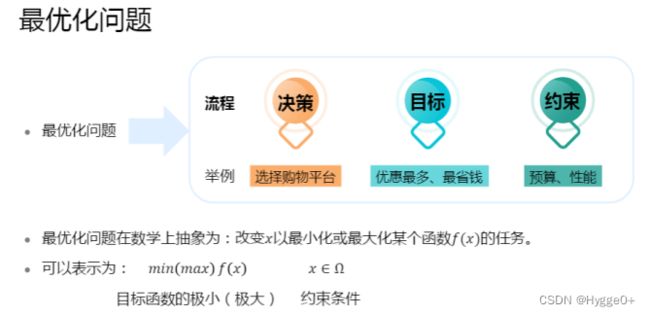
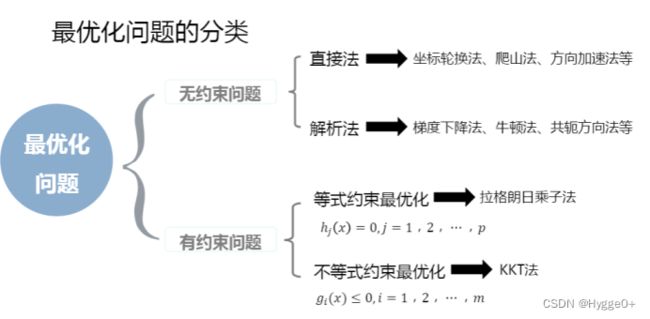
【最优化问题】

机器学习中的大多数问题都可以归结为最优化问题。最优化问题是求解函数极值的问题，包括极大值和极小值。在机器学习之类的实际应用中，我们一般将最优化问题统一表述为求解函数的极小值问题，即：

 

 

 

【补充说明】

举例：双十一优惠期间买台电脑

决策：在哪个店铺买

目标：实现最高优惠

约束：预算、以及购买电脑的性能

 

【补充说明】

直接法使用条件：目标函数比较复杂或写不出具体表达式时，通过数值计算，经过一定迭代过程产生点列，在其中搜索最优点。

解析法（间接法）：根据无约束问题的目标函数表达式给出一种求解最优解的方法。

 

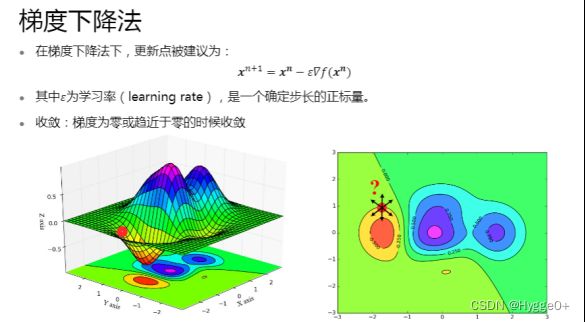
【为什么叫梯度下降算法？】

梯度方向是函数值增加最快的方向，所以梯度的负方向就是函数减小最快的方向。

一般情况下，我们训练模型是为了找到使目标函数（如损失函数）取得最小值时的参数。所以希望从某个初始值开始，函数值在参数的不断更新中逐渐减小，所以更新参数时总是沿着梯度方向的负方向前进，直至到最低点（即损失函数最小值）。

【梯度下降法公式推导】

根据泰勒公式可以得到如果x的变化很小，并且变化值与导数值反号，则函数值下降。

 

多元函数f(x)在x处的泰勒展开公式为：（忽略二次及更高项）

【注：其中是指梯度向量与自变量增量的内积，，等价于一元函数中的】

当Δx足够小时，在x邻域内可忽略二次及更高项，有

[该式呈现出函数增量、梯度与自变量增量之间的关系]

[注：对于一元函数来说，x的变化方向只有左和右；但对于多元函数来说，Δx是一个向量，其有无穷多个方向。那么如何确定函数递减（下山）的方向呢？]

【确定函数值下降时Δx的方向】

根据此式可知，若能保证，则可保证f(X)函数值递减，即往下坡这个正确方向走。

 

根据向量内积公式可知，上式等价于cosθ≤0 ，即选择合适的增量Δx，就能保证函数值下降，要达到这一目的，只要保证梯度和Δx的夹角的余弦值小于等于0就可以了。那么如何可以使函数值下降的最快呢？

 

【确定函数值下降最快时Δx的方向】

因为梯度方向是函数值增加最快的方向，所以在梯度相反的方向函数值下降的最快。当cosθ=-1（极小值）时，梯度与Δx反向，此时函数值下降最快。

此时，利用共线向量相关知识可将Δx表示为。【其中α为一个接近于0的正数，称为步长，由人工设定，用于保证x+Δx在x的邻域内，从而可以忽略泰勒展开中二次及更高的项】

 

此时函数变化量为。由该式可以得到，只要梯度不为0，往梯度的反方向走函数值一定是下降的。

 

迭代更新x值时，x=x-Δx,根据上面用梯度表示出的，可以得到迭代公式：

 

 

即从初始点X0开始，使用该迭代公式不断更新X值，只要没有到达梯度为0的点，则函数值会沿着序列Xk递减，最终会收敛到梯度为0的点，这就是梯度下降法。迭代终止的条件是函数的梯度值为0（实际实现时是接近于0），此时认为已经达到极值点。

附参考链接：梯度下降算法原理讲解_征途黯然.的博客-CSDN博客_梯度下降数学原理

 

【补充说明】

如果想要找到最短的路径到达最底部。梯度下降法每次只从当前位置选择一个坡度最大的方向往下走；而牛顿法在选择方向时不仅会考虑坡度是否足够大，而且还会考虑走了一步后坡度是否会变小。因此牛顿法往往会少走很多弯路，收敛速度会比梯度下降法更快。

 

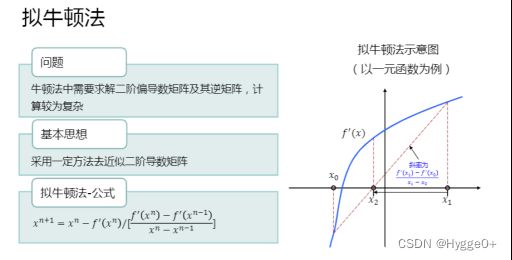
【补充说明】

牛顿法尽管收敛速度比较快，但每次更新迭代时都要计算二阶导数矩阵以及其逆矩阵，造成计算量偏大，且逆矩阵可能不可逆。故而提出拟牛顿法。将一阶导数两点连线的斜率来近似二阶导数。保证收敛速度的同时减少计算量。

 

 

【补充说明】

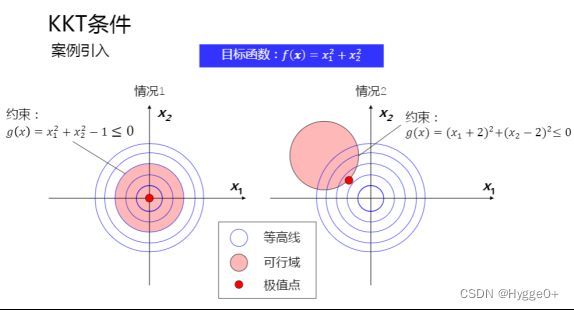
f(x)的取值区域为目标域（蓝色等高线），符合g(x)<=0的区域为约束域（红色区域）。

 

左图为约束无效；右图为约束有效

KKT法（不等式约束），是拉格朗日（等式约束）的扩展。约束有效时，将不等式约束条件转换为等式约束条件。

 

【约束是否有效】

【假设一条狗被绳子拴住，f(X)代表狗与食物之间的最短距离，约束域g(X)<=0为狗被绳子拴住的圆形区域】

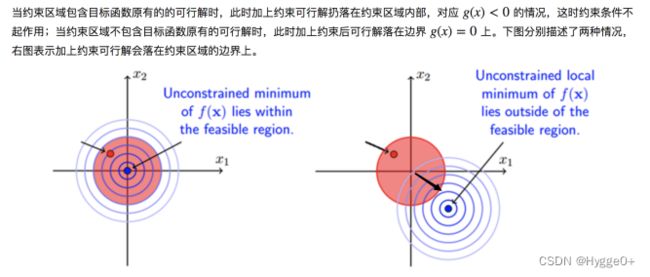
若f(X)本身的最小取值可行解包含在约束域内，即取到f(x)的局部最小值时若g(x)<0，则表示约束无效。【此情况为：狗本身就在食物区域内，不论是否被绳子拴住其都可以获得食物，即狗与食物之间的最短距离为0（此为目标域局部最小值），这表示狗并未被绳子真正约束】；

若f(X)最后的取值落在g(X)的边界，即g(x)=0，f(X)取到局部极小值，则表示约束有效。【此情况为：狗本身并不在食物区域内，被绳子拴住的狗只能尽可能缩短其与食物之间的距离，则表示狗被绳子约束。若未被约束的话，就可以到达食物区域，与其最短距离为0。在约束下狗尽力到达目标域某点，此点是f(x)尽可能小的位置，称为f(x)在这个约束下取到的最小值点，是另一种意义上的极小值点。】

正是因为这两种情况同时存在，所以才有了KKT条件。

【KKT条件】

 

附：参考博客链接

SVM（二）：KKT条件最直白的解释_CtrlZ1的博客-CSDN博客_svm的kkt条件