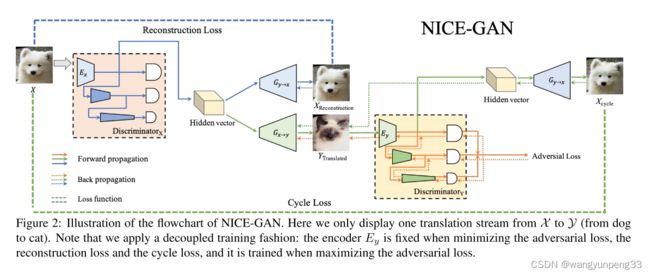
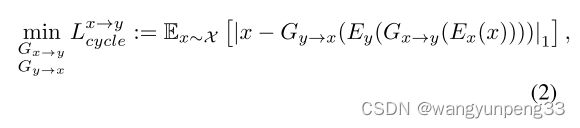【研究生工作周报】(NICE-GAN论文再回顾)
NICE-GAN
文章目录
- NICE-GAN
- 前言
- 一、图像翻译的问题定义
- 二、NICE-GAN各组件架构
-
- 1.多尺度判别器(Multi-Scale Discriminator)
- 2.残差注意力机制(Residual Attention)
- 3. 自适应混合归一化层(Adaptive layer-instance normalization)
- 可视化隐层编码(t-SNE)
- 三. 解耦训练机制
-
- Adversarial loss
- Cycle-consistency loss
- Reconstruction loss
- 四. 判别网络,生成网络架构总览
-
-
- 参考论文及博客
-
前言
早在假期就对这篇论文做过初步研究,但碍于当时在对抗生成网络这一领域的基础比较薄弱,所以对论文的理解比较肤浅。通过这段时间对CGAN,pix2pix,CycleGAN等经典GAN模型学习之后,在理论和实践层面对GAN有了一个比较系统的认识。本周就NICE-GAN模型进行一个理论上的总结。
一、图像翻译的问题定义
对于两个图像域 D o m a i n X Domain X DomainX和 D o m a i n Y Domain Y DomainY,
监督图像翻译:给定联合分布 p ( X , Y ) p(X,Y) p(X,Y),学习条件映射 f x → y = p ( Y ∣ X ) f_{x \rightarrow y} = p(Y|X) fx→y=p(Y∣X) 和 f y → x = p ( X ∣ Y ) f_{y \rightarrow x} = p(X|Y) fy→x=p(X∣Y)
而无监督图像翻译:给定边缘分布 p ( X ) p(X) p(X), p ( Y ) p(Y) p(Y);学习条件映射 f x → y = p ( Y ∣ X ) f_{x \rightarrow y} = p(Y|X) fx→y=p(Y∣X) 和 f y → x = p ( X ∣ Y ) f_{y \rightarrow x} = p(X|Y) fy→x=p(X∣Y)。
现在的问题是做无监督的图像翻译时,可以有无数个条件概率 p ( Y ∣ X ) p(Y|X) p(Y∣X) 和 p ( X ∣ Y ) p(X|Y) p(X∣Y) 服从相同的边缘分布 p ( X ) p(X) p(X) , p ( Y ) p(Y) p(Y) ,这也诠释了为什么衡量Cycle-GAN性能时会以pix2pix模型作为Top-line。为了解决这个问题,不同模型都有自己的策略:UNIT使用了weight-coupling,Cycle-GAN使用的cycle-consistency,identity-mapping-enforcing。
对于大多数现存的架构来说,翻译过程可以表述为:
编码器 E x E_{x} Ex和生成器 G x → y G_{x \rightarrow y} Gx→y组合实现图像的生成
y ′ = f x → y ( x ) = G x → y ( E x ( x ) ) y' = f_{x \rightarrow y}(x) = G_{x \rightarrow y}(E_{x}(x)) y′=fx→y(x)=Gx→y(Ex(x))
再拿判别器 D y D_{y} Dy 区分真实图像 y y y 和生成图像 y ′ y' y′ 。
( y → x y \rightarrow x y→x 同理, x ′ = f y → x ( y ) = G y → x ( E y ( y ) ) x' = f_{y \rightarrow x}(y) = G_{y \rightarrow x}(E_{y}(y)) x′=fy→x(y)=Gy→x(Ey(y)))
NICE-GAN模型使用判别器进行编码
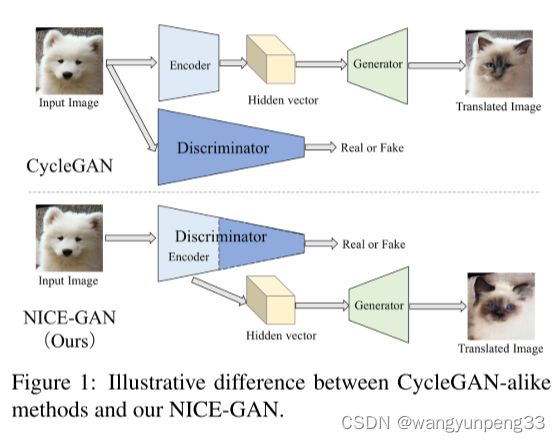
这里我们把判别器 D x D_{x} Dx 拆分成编码部分 E x D E^{D}_{x} ExD 和分类部分 C x D C^{D}_{x} CxD , E x D E^{D}_{x} ExD 会代替 f x → y f_{x \rightarrow y} fx→y 原始的编码器,得到一个新的翻译过程 y ′ = f x → y ( x ) = G x → y ( E x D ( x ) ) y' = f_{x \rightarrow y}(x) = G_{x \rightarrow y}(E^{D}_{x}(x)) y′=fx→y(x)=Gx→y(ExD(x))
( y → x y \rightarrow x y→x 同理, x ′ = f y → x ( y ) = G y → x ( E y D ( y ) ) x' = f_{y \rightarrow x}(y) = G_{y \rightarrow x}(E^{D}_{y}(y)) x′=fy→x(y)=Gy→x(EyD(y)))
新形成的分类组件 C x C_{x} Cx, C y C_{y} Cy 采用mutil-scale结构来增强表达能力。
新形成的编码组件 E x D E^{D}_{x} ExD 和 E y D E^{D}_{y} EyD 在翻译和判别的过程中都要参与训练,增加了训练难度,采用解耦训练策略。
二、NICE-GAN各组件架构
1.多尺度判别器(Multi-Scale Discriminator)
其实从名字就能大概猜出来应该是对输入的img做了多层特征的判别,也就是说传统的discriminator是对一张image做判别,但是Multiscale是多个传统discriminator的叠加。比如Multiscale中的第一个D是用来判别输入img的真假,第二个D是判别输入img经过下采样后的真假,以此类推。。。
Multi-Scale Discriminator首先被提出时,用于应对不同尺寸的输入图像。这篇论文里使用一种更有效的方式:
对于一个固定size的输入图像,我们把它在不同层经过卷积的特征图作为不同size的图像喂给对应size的分类器作判别。
2.残差注意力机制(Residual Attention)
为了促进特征在判别器中的传递,U-GAT-IT首次提出引入注意力机制。
设编码器包含 K K K个特征图 { E x k } k = 1 K \left\{{E^{k}_{x}}\right\}^{K}_{k=1} {Exk}k=1K ,引入一个注意力向量 ω \omega ω ,得到注意力特征图
α ( x ) = ω × E x ( x ) = { ω k × E x k ( x ) } k = 1 K \alpha(x) = \omega \times {E_{x}(x)} = \left\{ \omega_{k} \times {E^{k}_{x}(x)}\right\}^{K}_{k=1} α(x)=ω×Ex(x)={ωk×Exk(x)}k=1K
基于U-GAT-IT,进一步考虑一个残差连接,引入一个可训练参数 γ \gamma γ 来权衡
带权重的特征和原始特征
α ( x ) = γ × ω × E x ( x ) + E x ( x ) \alpha(x) = \gamma \times \omega \times {E_{x}(x)} + {E_{x}(x)} α(x)=γ×ω×Ex(x)+Ex(x)
( γ \gamma γ =0代表未激活参与特征,非0代表激活残差注意力机制,而且通过对不同数据集的训练发现, γ → 0 \gamma\rightarrow0 γ→0,代表更多关注全局特征,说明翻译图像的全部内容比局部细节更重要)
3. 自适应混合归一化层(Adaptive layer-instance normalization)
U-GAT-IT引入了自适应的LN和IN的混合归一化层,帮助我们的注意力引导模型在不修改模型架构或超参数的情况下灵活控制形状和纹理的变化量。
这里说一下Adaptive Layer-Instance Normalization的具体公式:
a ^ I = a − μ I σ I 2 + ϵ , a ^ L = a − μ L σ L 2 + ϵ \hat{a}_{I}=\frac{a-\mu_{I}}{\sqrt{\sigma_{I}^{2}+\epsilon}}, \hat{a}_{L}=\frac{a-\mu_{L}}{\sqrt{\sigma_{L}^{2}+\epsilon}} a^I=σI2+ϵa−μI,a^L=σL2+ϵa−μL
上面是IN和LN的归一化公式,然后将 a ^ I \hat{a}_{I} a^I和 a ^ L \hat{a}_{L} a^L代入到进行合并( γ \gamma γ和 β \beta β通过外部传入): AdaLIN ( a , γ , β ) = γ ⋅ ( ρ ⋅ a ^ I + ( 1 − ρ ) ⋅ a ^ L ) + β \operatorname{AdaLIN}(a, \gamma, \beta)=\gamma \cdot\left(\rho \cdot \hat{a}_{I}+(1-\rho) \cdot \hat{a}_{L}\right)+\beta AdaLIN(a,γ,β)=γ⋅(ρ⋅a^I+(1−ρ)⋅a^L)+β
为了防止 ρ \rho ρ超出[0,1]范围,对 ρ \rho ρ进行了区间裁剪:
ρ ← c l i p [ 0 , 1 ] ( ρ − τ Δ ρ ) \rho \leftarrow c l i p[0,1](\rho-\tau \Delta \rho) ρ←clip[0,1](ρ−τΔρ)
AdaIN能很好的将 cotents_feature 转移到 style_feature 上,但AdaIN假设特征通道之间不相关,意味着style_feature需要包括很多的内容模式,而LN则没有这个假设,但LN不能保持原始域的内容结构,因为LN考虑的是全局统计信息,所以作者将AdaIN和LN结合起来,结合两者的优势,有选择地保留或改变 c o t e n t s cotents cotents 信息,有助于解决广泛的图像到图像的翻译问题。
class adaILN(nn.Module): #Adaptive Layer-Instance Normalization代码
def __init__(self, num_features, eps=1e-5):
super(adaILN, self).__init__()
self.eps = eps
#adaILN的参数p,通过这个参数来动态调整LN和IN的占比
self.rho = Parameter(torch.Tensor(1, num_features, 1, 1))
self.rho.data.fill_(0.9)
def forward(self, input, gamma, beta):
#先求两种规范化的值
in_mean, in_var = torch.mean(torch.mean(input, dim=2, keepdim=True), dim=3, keepdim=True), torch.var(torch.var(input, dim=2, keepdim=True), dim=3, keepdim=True)
out_in = (input - in_mean) / torch.sqrt(in_var + self.eps)
ln_mean, ln_var = torch.mean(torch.mean(torch.mean(input, dim=1, keepdim=True), dim=2, keepdim=True), dim=3, keepdim=True), torch.var(torch.var(torch.var(input, dim=1, keepdim=True), dim=2, keepdim=True), dim=3, keepdim=True)
out_ln = (input - ln_mean) / torch.sqrt(ln_var + self.eps)
#合并两种规范化(IN, LN)
out = self.rho.expand(input.shape[0], -1, -1, -1) * out_in + (1-self.rho.expand(input.shape[0], -1, -1, -1)) * out_ln
#扩张得到结果
out = out * gamma.unsqueeze(2).unsqueeze(3) + beta.unsqueeze(2).unsqueeze(3)
return out
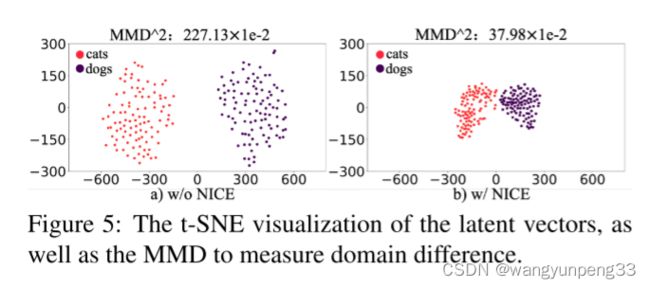
可视化隐层编码(t-SNE)
分析与结论:
通过t-SNE可视化隐层编码,并利用Maximum Mean Discrepancy(MMD)以计算隐层空间两个编码分布的差异。有趣的是,通过NICE的训练,两个域的隐层空间分布变得更加聚集和紧密,但彼此依然可分。这种现象解释了为什么NICE-GAN表现出色。基于共享隐层空间假设构建的NICE-GAN,通过缩短低维隐层空间中域之间的转换路径,可能会促进高维图像空间的域的转换。同时进一步支持了一个重要观点:对比由通过最大似然训练的编码器网络学习的特征,由经过判别训练的网络学习到的特征往往更具表现力,也更适合推理。在NICE-GAN中,编码器也成为分布距离度量函数的一部分,而生成器只需要从隐层分布中提取循环一致性信息并拟合目标域分布。
三. 解耦训练机制
由于我们将编码器 E x E_{x} Ex作为判别器 D x D_{x} Dx的一部分呢,它也同样作为生成器 G x → y G_{x\rightarrow y} Gx→y的输入,用传统训练方式会导致不一致。我们采用将编码器 E x Ex Ex的训练同生成器 G x → y G_{x\rightarrow y} Gx→y解耦。
Adversarial loss
LSGAN主要解决关键: 使用最小二乘损失代替交叉熵损失,来避免梯度消失和训练过程不稳定等缺陷。
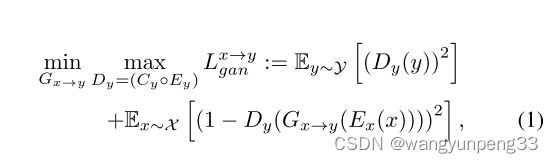
当 m i n G x → y L g a n x → y \underset{G_{x\rightarrow y}}{min}L^{{x\rightarrow y}}_{gan} Gx→yminLganx→y 时, E x E_{x} Ex 和 E y E{y} Ey 固定;
当 m a x D y L g a n x → y \underset{D_{y}}{max}L^{{x\rightarrow y}}_{gan} DymaxLganx→y 时, E x E_{x} Ex固定,训练 E y E_{y} Ey
Cycle-consistency loss
Reconstruction loss
Cycle-GAN考虑 identity loss 时有一个域相似性的假设,我们这里考虑Reconstruction loss时是共享隐藏空间的假设
在将源域的真实样本 x x x 的隐藏向量 E x ( x ) E_{x}(x) Ex(x) 作为生成器 G x → y G_{x\rightarrow y} Gx→y 的输入时,考虑到重构损失。
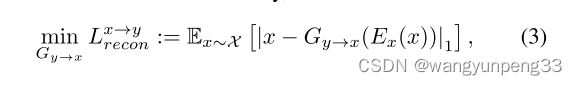
判别器的总损失:
m a x E x , C x , E y , E y λ 1 L g a n \underset{E_{x},C_{x},E_{y},E_{y}}{max}\lambda_{1} L_{gan} Ex,Cx,Ey,Eymaxλ1Lgan
生成器的总损失:
m i n G x → y , G y → x λ 1 L g a n + λ 2 L c y c l e + λ 3 L r e c o n \underset{G_{x\rightarrow y},G_{y\rightarrow x}}{min}\lambda_{1} L_{gan}+\lambda_{2} L_{cycle}+\lambda_{3} L_{recon} Gx→y,Gy→xminλ1Lgan+λ2Lcycle+λ3Lrecon
( L g a n = L g a n x → y + L g a n y → x L_{gan} = L^{{x\rightarrow y}}_{gan} + L^{{y\rightarrow x}}_{gan} Lgan=Lganx→y+Lgany→x, L c y c l e = L c y c l e x → y + L c y c l e y → x L_{cycle} = L^{{x\rightarrow y}}_{cycle} + L^{{y\rightarrow x}}_{cycle} Lcycle=Lcyclex→y+Lcycley→x, L r e c o n = L r e c o n x → y + L r e c o n y → x L_{recon} = L^{{x\rightarrow y}}_{recon} + L^{{y\rightarrow x}}_{recon} Lrecon=Lreconx→y+Lrecony→x)
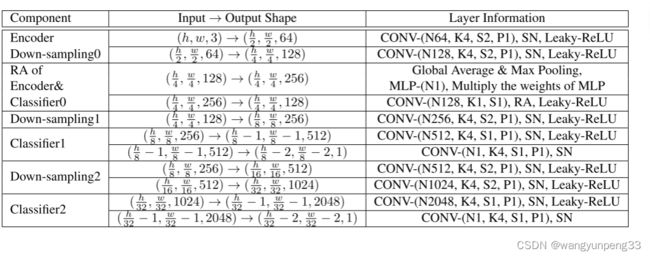
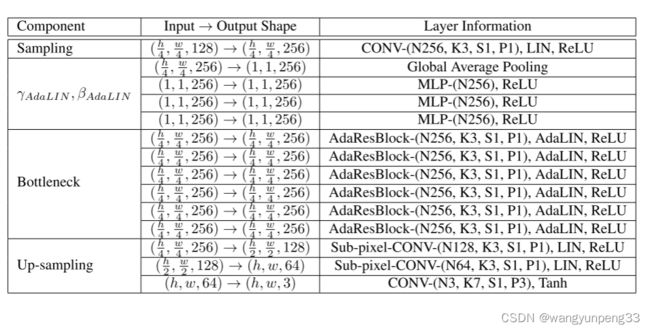
四. 判别网络,生成网络架构总览
参考论文及博客
Least Squares Generative Adversarial Networks(LSGANs)
paper / note
Residual Attention Network for Image Classification
paper / blog
Adaptive Instance Normalization(AdaIN)
paper / note
Unsupervised Generative Attentional Networks with Adaptive Layer-Instance Normalization for Image-to-Image Translation (U-GAT-IT)
paper / note
深度学习中的五种归一化(BN、LN、IN、GN和SN)