【知识图谱综述】Knowledge Graphs: A Survey

知识图谱综述

本文主要在阅读文章Knowledge Graphs. ACM Comput. Surv., 54(4): 1–37. 2021的基础上进行归纳总结，涉及原理知识较浅，旨在帮助对知识图谱进行较全面的理解。如有错误，还请不吝赐教。

1. Intro

现代"knowledge graph"概念起源：2012 announcement of the Google Knowledge Graph

相关参考文献

知识图谱相关实例https://github.com/knowledge-graphs-tutorial/examples.

术语

• Knowledge graph: a graph of data intended to accumulate and convey knowledge of the real world, whose nodes represent entities of interest and whose edges represent potentially different relations between these entities. 其中数据图符合基于图的数据模型（有向边标记图、异构图、属性图等）。
• Knowledge: “explicit knowledge”, something that is known and can be written down.
• Open vs. enterprise knowledge graphs: 根据组织或社区的不同区分

2. Data Graphs

图数据的建模是构造任何知识图谱的基础

Models

最常用的图数据模型

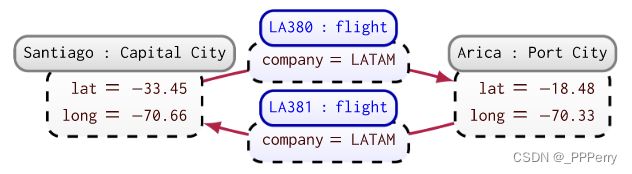
• 有向边标记图 (del graph, or multi-relational graph): 节点和节点间的有向标记边。节点表示实体，边表示实体间的二元关系。
  特点：灵活，不需要像树一样分层组织数据，也可以表示循环

• 异构图：每个节点和边都被分配一种类型。
  

• 同质边：位于两个相同type节点之间；否则为异质边。允许根据type对节点分区，可用于机器学习任务。但是不同于del graph，节点和类型只能一对一。

• 属性图：节点和边可以关联属性值和标签，建模和修改时相比del graph更加灵活。

• 图数据集：管理多个graph，包括一组named graphs和一个default graph。
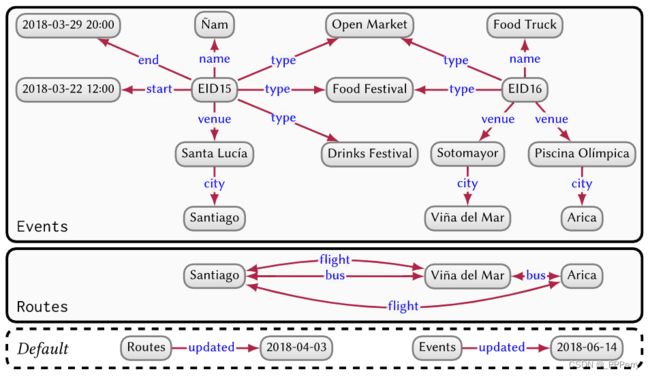
  默认图没有ID，管理命名图的元数据。图数据集可推广至任何类型的graph，不限于del graph。

Querying

查询图的语言：SPARQL for del graphs、Cypher、Gremlin、G-CORE for property graphs 等。

Graph Patterns：用于查询的图结构，包含常量和变量，变量即查询中进行匹配的变量。
左图为图模式，右图为该图模式对图数据的映射。即图模式将图数据转换为映射的结果表。

在右图后三行中，vn1和vn2的内容相同的，这种查询结果也许是我们不想要的。因此，诞生了多种用于评估图模式的语义，其中最重要的两种：基于同态的语义(homomorphism-based semantics)，允许不同变量mapping到同一术语，即右图所有映射都是返回的结果（SPARQL采用此语义）；基于同构的语义(isomorphism-based semantics)，不同变量不能映射到相同术语。

除此之外，还有支持SQL各种运算符或图形查询语言的复杂图模式，以及用于正则路径查询的导航图模式等。

总之作用就是想办法设计图模式，从图数据中返回需要的映射表。

Validation

虽然图为大规模的各种不完整数据提供了灵活的表示，但我们可能希望验证我们的数据图遵循特定的结构或在某种意义上是“完整的”。 例如，我们可能希望确保所有事件都至少有一个名称、地点、开始和结束日期。 验证的一种机制是使用形状图。

形状图由一组相互关联的形状组成，形状是以数据图中的一组节点为目标，并指定对这些节点的约束。类似UML类图。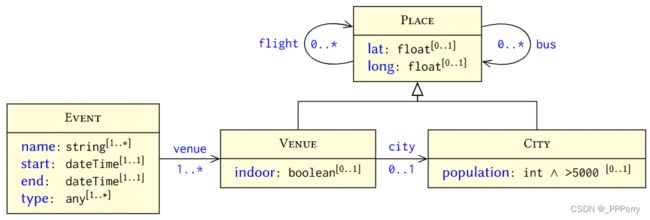

Context

上下文包含了数据的隐含信息，例如发生的时间地点等，允许从不同的角度解释数据。

对于数据的上下文信息，可以直接将上下文作为数据节点，也可以定义边的信息等，如下图所示，e作为边而非直接表示中的数据节点。

3. Deductive Knowledge

这部分包含较多规范标准，实际应用场景下涉及到的不多，这里简略概括。

我们可以从数据图中推断出更多的知识，比如在第一张图中，推断出音乐节在圣地亚哥等。给定作为前提的数据和一些我们可能知道的关于世界的先验规则，我们可以使用演绎过程来推导出新数据。

通过给定机器形式化的逻辑结果，就可以实现自动化推理。尽管我们可以利用许多逻辑框架来实现这些目的，例如First-order Logic, Datalog, Prolog, Answer Set Programming等，但我们关注的是知识本身（ontologies），可以看作是具有明确含义的知识图谱。

Ontologies

知识本体（ontology）是一种表示形式，是一种对知识术语具体的、形式化的表示方法。最流行的本体语言是Web Ontology Language（OWL）。

在ontology中，节点和边都可以映射到我们现实生活的解释意义上，得到的解释映射图称为域图，应该和原来的数据图结构是完全一致的。

对于解释，也同样存在多种假设（assumtions）的标准，比如Closed World Assumption (CWA)/Open World Assumption (OWA)、Unique Name Assumption (UNA)/No Unique Name Assumption (NUNA)（比如同样的实体可以有不同名称等）等。

除了假设外，我们还可以定义数据图中的一些模式，以及满足该模式的相关解释。比如对实体、属性甚至类等，都可以定义特定的模式，从而依据模式发掘符合的解释信息。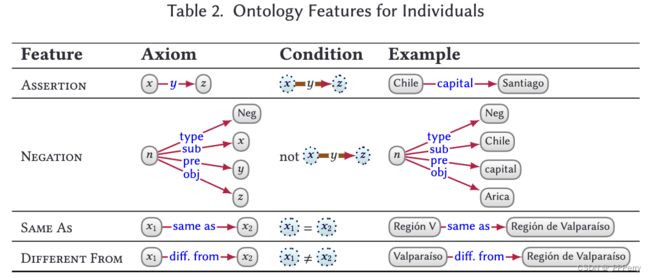

Reasoning

OWL标准中还定义了推理规则，给出了多种推理的实现方式。OWL标准也受到较多逻辑描述Description Logics (DLs)的影响，后者可以看作是知识图谱的前身。

4. INDUCTIVE KNOWLEDGE

归纳推理可以从输入的数据中概括出模式，这些模式可以用来生成新的但可能不精确的预测。

例如，从包含地理和航班信息的图中，我们可以观察到几乎所有国家的首都都有国际机场，因此预测，因为圣地亚哥是首都，它可能也有一个国际机场； 但是，一些首都（例如瓦杜兹）没有国际机场。 因此，预测不一定是完全准确的。假如我们看到195个首都中187个有国际机场，那么我们就可以为使用该模式做出的预测指定0.959的置信度。

我们将通过归纳获得的知识称为归纳知识（inductive knowledge），包括概括出的模型和这些模型所做的预测。

有监督和无监督学习常用于知识图谱的归纳技术中，如图所示。
在图分析中，有大量工作是用无监督方法的，比如检测社区或集群，在图中找到中心节点和边等。图嵌入使用自监督来学习知识图谱中的低维数值模型。图结构也可以通过图神经网络直接用于监督学习。符号学习可以通过自监督的方式从图中学习符号模型，即规则或公理形式的逻辑公式等。

Graph Analytics

图算法一般用于分析图的拓扑，例如节点和组是如何连接的等等。在本节中，我们会介绍应用于知识图谱的常见图算法，以及可以实现此类算法的图形处理框架。

Graph Algorithms

• 中心性分析(centrality analysis)：识别图中最重要的点和边。具体的节点中心性度量包括度、介数、接近度、特征向量、PageRank、HITS、Katz等。其中介数度量中心性也可以应用于边，比如通过寻找短路线中最依赖的边来预测最繁忙的交通路段等，

• 社区检测(community detection)：识别内部连接更紧密的子图。包括最小割算法、标签传播、Louvain模块化等。

• 连通性分析(connectivity analysis)：估计图的连通性和弹性。包括测量图密度或k连通性、检测强/弱连通分量、计算生成树或最小割等。

• 节点相似性(node similarity)：通过节点在邻域内的连接方式来找到相似的节点。包括使用结构等价、随机游走、扩散核等方法度量相似性。这些方法可以帮助我们更好的理解连接节点的内容以及它们相似的方式。

• 图摘要(graph summarisation)：从图中提取高级结构，通常用于商图(quotient graphs)。这样的方法有助于为大规模图提供概览。示例如图所示。
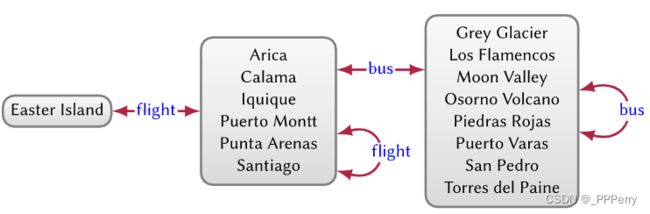
  在这种情况下，商节点是根据传出边标签定义的，例如，我们概括出从左到右分别代表岛屿、城市和城镇。

针对简单图或没有edge label的有向图，已经提出并研究了许多此类图算法。在知识图谱的背景下，一个挑战就是如何将此类算法应用于del图、异构图或属性图等知识图谱模型。

Graph Processing Frameworks

对于大规模处理任务，已经提出了许多并行图框架，比如Apache Spark (GraphX)、GraphLab、Pregel、Signal–Collect、Shark等。这些框架采用迭代计算，每个节点读取入边的消息（可能还有它的上一个状态），执行计算后再向出边发送结果。

一个在并行图框架上进行PageRank迭代算法的示例如图所示。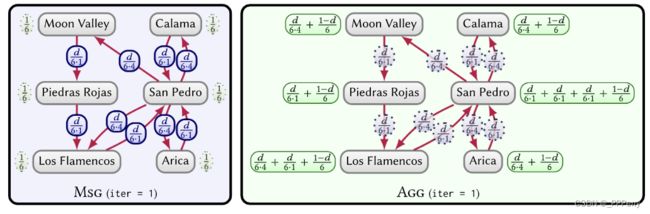
此框架中的算法由计算消息值(MSG)和累积消息(AGG)的函数组成。

Knowledge Graph Embeddings

机器学习可直接用于提炼知识图谱；或用于知识图谱的下游任务，例如推荐、信息提取、问答、查询松弛、查询近似等。 然而，机器学习技术通常采用数字表示（例如向量），这与图的表示方式通常是不同的。 那么，如何对图进行数字编码以进行机器学习呢？

最开始的尝试是使用独热码，为每个节点都创建一个$L\times V$的矩阵，$L$代表边的标签种类数量，$V$代表点的数量。

这里为什么不用点乘点的矩阵？因为不同于常见图模型，知识图谱中不同点之间可能存在多条标签边。

然而，这样表示会导致稀疏且过大的矩阵，对大多数机器学习模型来说都过于复杂。

知识图谱嵌入技术的主要目标是在连续的低维（维数固定，通常很低）向量空间中创建图的密集表示（即嵌入图），从而可以用于机器学习任务。

为了获得嵌入模型，根据给定的评分函数，我们需要最大化正边（通常是图中的边）的合理性并最小化负例的合理性（通常是图中节点或边标签发生变化就使得它们不再在图中的边）。 然后可以将生成的嵌入视为通过自我监督学习的模型，该模型对图的（潜在）特征进行编码，将输入的边映射到合理性的分数。

嵌入可以用于许多下游任务。合理性评分函数可用于为边分配置信度或预测缺失的连接。 此外，嵌入通常会将相似的向量分配到相似的术语，因此也可以用于相似性度量。

接下来我们将讨论一些最常用的图嵌入技术。

Translational Models

翻译模型将边标签解释为从头节点到尾节点的转换。例如
，就可以认为是bus标签将San Pedro转换为了Moon Valley。

翻译模型的开创性方法是TransE。对于上述的正边，TransE就会学习到向量${\mathbf{e}}_S$，${\mathbf{r}}_b$和${\mathbf{e}}_M$，并使得${\mathbf{e}}_S+{\mathbf{r}}_b$尽可能的接近${\mathbf{e}}_M$。对于负边，就让两向量和尽可能的远离。下图是TransE对一个二维图的关系和实体的嵌入表示。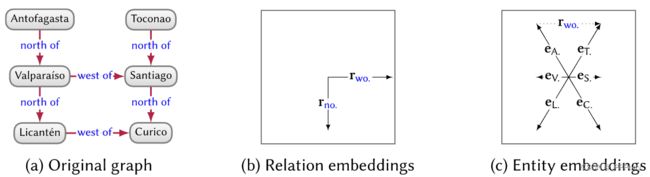
为了防止TransE算法给不同的边分配相似的向量，也有很多使用超平面或不同向量空间的技术对算法进行改进。

Tensor Decomposition Models

张量（Tensor）是一个多维数值字段，它可以将标量（0阶张量）、向量（1阶张量）和矩阵（2阶张量）推广到任意维度。张量分解涉及将张量分解为更多低维张量，原始张量可以通过这些低维张量固定的基本操作序列重新组合（或近似）。这些张量可以看作是在原始张量中捕获潜在因素。关于张量分解的方法有很多，现在我们将简要介绍张量分解背后的主要思想。

给定一个$a\times b$ 矩阵$C$，其中每个元素$C_{ij}$代表了第$i$个城市第$j$个月的平均温度。我们可以将矩阵分解为一个长度为$a$的向量$x$（纬度较低的城市温度较低）和长度为$b$的向量$y$（秋冬的月份温度较低），如果恰有$C=x\times y$，则$C$为秩为1的矩阵。否则，秩就是表示矩阵$C$所需最小向量乘积和的数量，即$C=x_1\times y_1+\cdots +x_r\times y_r$。后面向量乘积可能对应城市高度的矫正、更高温度的变化等等多种因素。矩阵的秩分解就是设置一个限制$d$，计算$d$个向量乘积的和，给出最好的矩阵的$d$秩逼近。我们把这个思想推广到张量的低秩分解，这就是规范多元分解方法（Canonical Polyadic）（CP）。

对于知识图谱来说，我们可以定义一个三维独热编码矩阵，代表点-标签边-点，然后分解成多个三向量乘积的和，如下图所示。
但是，我们知识图谱嵌入的目标通常是为每个实体分配一个向量。

DisMult是基于秩分解计算知识图谱嵌入的开创性方法，其中每个实体和关系都与维度为$d$的向量相关联，因此对于边
，设计一个合理性评分函数${\sum }_{i=1}^d{\left({\mathbf{e}}_{\mathrm{s}}\right)}_i{\left({\mathbf{r}}_{\mathrm{p}}\right)}_i{\left({\mathbf{e}}_{\mathrm{o}}\right)}_i$，目标就是学习每个节点和边的向量，以最大化正边的合理性并最小化负边的合理性。但是这个方法有一个不足之处，$s$指向$o$的评分函数和$o$指向$s$的评分函数是相同的，即没有办法捕获边的方向信息。

RESCAL使用矩阵代替向量作为关系嵌入，从而保留了边的方向性，但是计算空间和时间都远超DistMult方法。ComplEx使用复向量，HolE使用循环相关因子（实数）来保留边的方向。其他分解方法还有SimplE和TuckER等。其中TuckER是目前在benchmarks上的SOTA方法。

Neural Models

许多方法使用神经网络来学习具有非线性评分函数的知识图嵌入。

除了MLP外，也有如ConvE、HypER等卷积方法不断学习权重，从而根据权重参数生成一种对独热码向量的一种嵌入表示方法。

Language Models

表示自然语言的方法就是经典的嵌入方法，比如word2vec和GloVe等。

同样，语言嵌入的方法也可以应用于图。RDF2Vec在图上执行有偏差的随机游走，并将遍历的路径记录为“句子”，然后将其作为输入输入到word2vec模型中。KGloVe基于GloVe模型。就像原始的 GloVe 模型认为在文本窗口中频繁出现的单词更相关，KGloVe使用个性化的PageRank来确定与给定节点最相关的节点，然后将其结果输入GloVe模型。

Entailment-aware Models

到目前为止，嵌入只考虑数据图。 但是如果提供了一组规则的先验知识呢？ 我们就可以首先考虑使用约束规则来细化嵌入所做的预测。例如，如果我们定义一个事件最多可以有一个场地值，那么将多个场地分配给一个事件的边的合理性就会降低。

最近的方法更倾向于提出同时考虑数据图和规则的联合嵌入，例如FSL和KALE等。

Graph Neural Networks

相比于将图表示为数学向量，另一种方法是为图定义自定义的机器学习架构。大多数此类架构都基于神经网络。然而，传统神经网络往往拓扑结构较为均匀，而图的拓扑结构通常更加异构。

**graph neural network (GNN)**是一种神经网络，与嵌入不同，GNN支持针对特定任务的端到端监督学习：给定一组标记示例，GNN可用于对图的元素或图本身进行分类。GNN已被用于对图编码化合物、图像中的对象、文档等进行分类，以及预测流量、构建推荐系统、验证软件等。给定带标签的示例，GNN甚至可以取代图算法，例如，GNN 已被用于以监督方式查找知识图谱中的中心节点等。

我们将介绍两种 GNN：递归和卷积。

Recursive Graph Neural Networks

递归图神经网络 (Recursive graph neural networks) (RecGNNs)是图神经网络的开创性工作。它将有向图作为输入，节点和边与静态特征向量相关联，静态特征向量可以捕获节点和边标签、权重等。 图中的每个节点还具有一个状态向量，该状态向量根据来自节点邻居的信息（即相邻节点和边的特征和状态向量）使用参数转换函数进行递归更新。 然后，参数输出函数根据节点自身的特征和状态向量计算节点的最终输出。 这些函数递归地应用到一个固定点。 给定图中的部分标记节点集，可以使用神经网络来学习这两个参数函数。 因此，结果可以被视为递归（甚至是循环）神经网络架构。

举例说明如图所示。
在图中，节点用特征向量$n_x$（对节点类型的独热编码）和$t$时刻的隐藏状态$h_x^{(t)}$进行注释，而边用特征向量$a_{xy}$（标签类型的独热码) 注释。右侧的$f$和$g$函数即分别对应参数转换函数和参数输出函数。为了训练网络，我们可以标记哪些地方有旅游局，哪些没有，这些标签可以来自知识图谱，也可以人为标记。然后GNN学习两个参数$w$和$w^{\prime }$，随后就可以用于标记其他节点。

Convolutional Graph Neural Networks

GNN和CNN都是在输入数据的局部区域上工作：GNN在图中的节点及其邻居上运行。遵循这个直觉，许多卷积图神经网络 (ConvGNNs)，又名graph convolutional networks (GCNs)都被提出，其中转换函数就是通过卷积实现的。

CNN的一个好处是可以将相同的内核应用于图像的所有区域，但ConvGNN却不行，因为与图像的情况不同，图像的像素具有可预测数量的邻域，但是图中的节点可以是多种多样的。 解决这些挑战的方法涉及使用图的光谱表示，从图中诱导出更规则的结构。 另一种方法是使用注意力机制来学习特征对当前节点最重要的节点。

除了架构方面外，RecGNN 和 ConvGNN 之间还有两个主要区别。

1. RecGNN递归地将来自邻居的信息聚合到一个固定点，而ConvGNN通常应用固定数量的卷积层。
2. RecGNN通常在统一的步骤中使用相同的函数/参数，而ConvGNN 的不同卷积层可以在每个不同的步骤中应用不同的内核/权重。

Symbolic Learning

迄今为止讨论的监督学习难以解释数值模型，做出合理预测的原因隐含在学习参数的复杂矩阵中。同时，嵌入也受到词汇表问题的影响，它们通常无法为先前未见过的节点或边的输入提供结果。 一种解决方法是使用符号学习来以逻辑（符号）语言解释正边和负边的假设。这样的假设是可以解释的。此外，它们是可以量化的（例如，“所有机场都是国内的或国际的”），部分解决了词汇表的问题。

知识图谱的符号学习形式主要有两种：用于学习规则的规则挖掘和用于学习其他形式逻辑公理的公理挖掘。这部分主要与第三章中的规则和逻辑语言相对应，实际应用较少。

Rule Mining

规则挖掘一般指从大量的背景知识集合中以规则的形式发现有意义的模式。

虽然已经使用归纳逻辑编程 （ILP）探索了关系设置的类似任务，但在处理不完整的知识图时（在 OWA 下），如何定义负边尚不清楚。 一种常见的启发式方法是采用部分完整性假设（PCA）。

一个有影响力的图规则挖掘系统是AMIE，它采用 PCA 置信度度量并以自上而下的方式构建规则 。后来的工作建立在这些技术的基础上，从知识图谱中挖掘规则。

另一个研究方向是关于可微规则挖掘（differentiable rule mining），它通过使用矩阵乘法对规则体中的连接进行编码来实现规则的端到端学习。

Axiom Mining

除了规则之外，可以从知识图谱中挖掘出更通用的公理形式——用逻辑语言（如 DLs）表示。 我们可以将这些方法分为两类：挖掘特定公理（例如不相交公理disjointness axioms等）或一般公理（DL-Learner等）的方法。

5. Summary and Conclusion

知识图谱是组织或社区内知识的共同基础，能够随着时间的推移表示、积累、管理和传播知识 。 知识图谱已被应用于各种用例，从商业应用（涉及语义搜索、用户推荐、会话代理、针对性广告、交通自动化等）到为公共利益提供的开放知识图谱。 总体趋势包括：

• 使用知识图谱来大规模整合和利用来自不同来源的数据
• 结合演绎（规则、本体等）
• 归纳技术（机器学习、分析等）来表示和积累知识

除了特定主题之外，知识图谱更普遍的挑战包括可扩展性，尤其是演绎和归纳推理；质量，不仅在数据方面，而且在从知识图谱中得出的模型方面； 多样性，例如管理上下文或多模式数据； 动态性，考虑时间或流数据； 最后是可用性，这是提高采用率的关键。尽管人们在不断提出技术来准确解决这些挑战，但它们不太可能完全解决；相反，它们是作为知识图谱及其技术、工具等将继续成熟的维度指标。