Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs 阅读笔记
我的博客链接
0. 导读
0.1 文章是关于什么的?(what?)
知识图谱,图神经网络,关系预测,链接预测,图注意力模型
0.2 要解决什么问题?(why?)
- 基于CNN的嵌入模型独立的处理三元组,导致无法覆盖在三元组周围的本地邻居中固有隐含的复杂和隐藏信息。
- 随着模型深度的增加,远方实体的贡献呈指数下降。
0.3 用什么方法解决?(how?)
- 将不同的权重(注意力)分配给附近的节点,并通过迭代方式通过层传播注意力。
- 提出的关系组合在n跳邻居之间引入辅助边,这样就很容易允许实体之间的知识流。
- 作者设计一个encoder-decoder模型(坐着的生成图注意力模型和ConvKB的组合)
0.4文章有什么创新?
- 作者是第一个学习新的基于图注意力的嵌入,这些嵌入专门针对KG的关系预测。
0.5 效果如何?
基于流行的Freebase(FB15K-237)数据集上Hits @ 1指标的最新方法,作者的方法实现了104%的改进。
0.6 还存在什么问题?
- 分步训练编解码器,容易产生错误传播
- 需要transE作为初始嵌入。
- 这明明是链接预测,咋整个关系预测,这里可能有笔误
- 该方法无法以自上而下的递归方式捕获信息
1 背景知识
2 模型
2.1 Graph Attention Networks (GATs) 图注意力网络
一个单一的GAT层可以表示为:
e i j = a ( W x i → , W x j → ) e_{i j}=a\left(\mathbf{W} \overrightarrow{x_{i}}, \mathbf{W} \overrightarrow{x_{j}}\right) eij=a(Wxi,Wxj)
- 其中 e i j e_{ij} eij是边 ( e i , e j ) (e_i, e_j) (ei,ej)的注意力值, W \mathbf{W} W是线性变换矩阵(把输入特征映射到高维输出特征空间), a a a是注意力函数
节点 e i e_i ei的的GAT输出特征向量为:
x i ′ → = σ ( ∑ j ∈ N i α i j W x j → ) \overrightarrow{x_{i}^{\prime}}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \overrightarrow{x_{j}}\right) xi′=σ⎝⎛j∈Ni∑αijWxj⎠⎞
- 其中 α i j \alpha_{ij} αij是 e i j e_{ij} eij,其中 a a a使用了softmax函数
作者使用了多头注意力的方式去加固学习过程:
x i ′ → = ∥ k = 1 K σ ( ∑ j ∈ N i α i j k W k x j → ) \overrightarrow{x_{i}^{\prime}}=\|_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \overrightarrow{x_{j}}\right) xi′=∥k=1Kσ⎝⎛j∈Ni∑αijkWkxj⎠⎞
- 其中 k k k代表第 k k k个头, ∥ \| ∥代表一个串联。(这是第一种连接方式)
最后的输出结果取得是多头注意力的平均值,即
x i ′ → = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k x j → ) \overrightarrow{x_{i}^{\prime}}=\sigma\left(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \overrightarrow{x_{j}}\right) xi′=σ⎝⎛K1k=1∑Kj∈Ni∑αijkWkxj⎠⎞
- 这是第二种连接方式。
2.2 引入关系的重要性
GAT在处理过程中其实忽略了知识图谱中的关系,节点的关系十分重要。作者提出了一个整合节点特征和关系的注意力机制。(所以其实上面写的是GAT的流程,下面写的才是作者实际采用的方式,所以其实可以忽略上面写的直接看下面的也可以)
作者把尸体嵌入表示为一个矩阵 H ∈ R N e × T \mathbf{H} \in \mathbb{R}^{N_{e} \times T} H∈RNe×T,相似的关系嵌入表示为 G ∈ R N r × P \mathbf{G} \in \mathbb{R}^{N_{r} \times P} G∈RNr×P, T T T和 P P P分别为实体特征和关系特征的维度。
作者把三元组 t i j k = ( e i , r k , e j ) t_{i j}^{k}=\left(e_{i}, r_{k}, e_{j}\right) tijk=(ei,rk,ej)表示为:
c i j k → = W 1 [ h ⃗ i ∥ h ⃗ j ∥ g ⃗ k ] c_{i j k}^{\rightarrow}=\mathbf{W}_{1}\left[\vec{h}_{i}\left\|\vec{h}_{j}\right\| \vec{g}_{k}\right] cijk→=W1[hi∥∥∥hj∥∥∥gk]
- 其中, h ⃗ i , h ⃗ j , and g ⃗ k \vec{h}_{i}, \vec{h}_{j}, \text { and } \vec{g}_{k} hi,hj, and gk分别代表实体 e i , e j , r k e_{i}, e_{j}, r_{k} ei,ej,rk的嵌入表示。
作者参考Veliˇckovi´c et al., 2018)的方式是,为三元组设计了一个值来表示三元组的重要性:
b i j k = LeakyReLU ( W 2 c i j k ) b_{i j k}=\text { LeakyReLU }\left(\mathbf{W}_{2} c_{i j k}\right) bijk= LeakyReLU (W2cijk)
同样,作者给予了不同关系一个注意力值:
α i j k = softmax j k ( b i j k ) = exp ( b i j k ) ∑ n ∈ N i ∑ r ∈ R i n exp ( b i n r ) \begin{aligned} \alpha_{i j k} &=\operatorname{softmax}_{j k}\left(b_{i j k}\right) \\ &=\frac{\exp \left(b_{i j k}\right)}{\sum_{n \in \mathcal{N}_{i}} \sum_{r \in \mathcal{R}_{i n}} \exp \left(b_{i n r}\right)} \end{aligned} αijk=softmaxjk(bijk)=∑n∈Ni∑r∈Rinexp(binr)exp(bijk)
图3展示了 α i j k \alpha_{i j k} αijk的机制:
所以一个实体 e i e_i ei的新嵌入表示为:
h i ′ → = σ ( ∑ j ∈ N i ∑ k ∈ R i j α i j k c i j k ) \overrightarrow{h_{i}^{\prime}}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \sum_{k \in \mathcal{R}_{i j}} \alpha_{i j k} c_{i j k}\right) hi′=σ⎝⎛j∈Ni∑k∈Rij∑αijkcijk⎠⎞
同样,作者采用多头注意力机制:
h i ′ → = ∥ m = 1 M σ ( ∑ j ∈ N i α i j k m c i j k m ) \overrightarrow{h_{i}^{\prime}}=\|_{m=1}^{M} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j k}^{m} c_{i j k}^{m}\right) hi′=∥m=1Mσ⎝⎛j∈Ni∑αijkmcijkm⎠⎞
- 这里实际是图4中1所示部分。
作者采用一个线性变化来获得关系嵌入矩阵:
G ′ = G . W R G^{\prime}=G . \mathbf{W}^{R} G′=G.WR
- 其中, W R ∈ R T × T ′ \mathbf{W}^{R} \in \mathbb{R}^{T \times T^{\prime}} WR∈RT×T′。
- 这里是图4中2所示的部分。
- 感觉这里是因为关系嵌入在传播的过程中没有发生变化,强行线性变化使得发生变化。
在最后一层(Graph Attention Layer 2),作者作者将多头注意力进行取平均操作:
h i ′ → = σ ( 1 M ∑ m = 1 M ∑ j ∈ N i ∑ k ∈ R i j α i j k m c i j k m ) \overrightarrow{h_{i}^{\prime}}=\sigma\left(\frac{1}{M} \sum_{m=1}^{M} \sum_{j \in \mathcal{N}_{i}} \sum_{k \in \mathcal{R}_{i j}} \alpha_{i j k}^{m} c_{i j k}^{m}\right) hi′=σ⎝⎛M1m=1∑Mj∈Ni∑k∈Rij∑αijkmcijkm⎠⎞
- 这里是图4中4所示的部分
作者把初始的实体表示矩阵做了一个线性变换,如图4中3所示。即 W E H t \mathbf{W}^{E} \mathbf{H}^{t} WEHt操作。
作者把图4中3和4连接在一起以一下灯饰表示:
H ′ ′ = W E H t + H f \mathbf{H}^{\prime \prime}=\mathbf{W}^{E} \mathbf{H}^{t}+\mathbf{H}^{f} H′′=WEHt+Hf
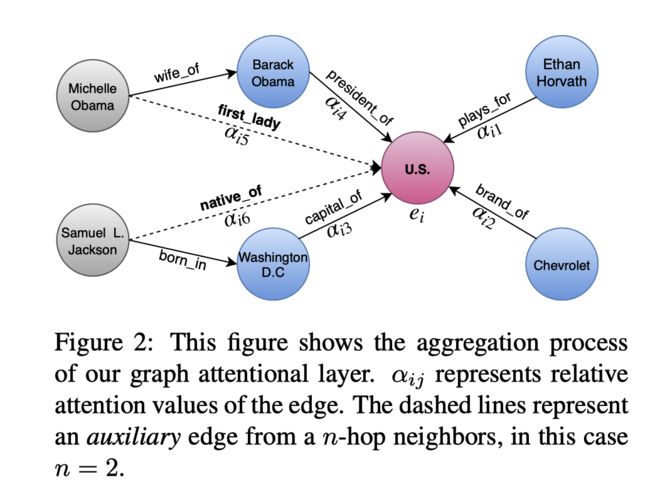
作者引入辅助关系路径
如图所示,作者强行建立了多跳关系实体的直接连接。
辅助关系的嵌入为有向路径中所有关系的嵌入和。
这里作者这个辅助边描述的不够清晰,弄得搞不懂这个辅助边在作者的数据集中是不是已经手动建立了,还是不存在。但是通过图中分配了权重说明作者是建立这个辅助边的。
2.3 训练目标
作者借鉴transE的思想 h ⃗ i + g ⃗ k ≈ h ⃗ j \vec{h}_{i}+\vec{g}_{k} \approx \vec{h}_{j} hi+gk≈hj,使用L1距离计算方式得到:
d t i j = ∥ h i → + g k → − h j → ∥ 1 d_{t_{i j}}=\left\|\overrightarrow{h_{i}}+\overrightarrow{g_{k}}-\overrightarrow{h_{j}}\right\|_{1} dtij=∥∥∥hi+gk−hj∥∥∥1
- 其中 t i j k = ( e i , r k , e j ) t_{i j}^{k}=\left(e_{i}, r_{k}, e_{j}\right) tijk=(ei,rk,ej)
作者采用hinge-loss:
L ( Ω ) = ∑ t i j ∈ S ∑ t i j ′ ∈ S ′ max { d t i j ′ − d t i j + γ , 0 } L(\Omega)=\sum_{t_{i j} \in S} \sum_{t_{i j}^{\prime} \in S^{\prime}} \max \left\{d_{t_{i j}^{\prime}}-d_{t_{i j}}+\gamma, 0\right\} L(Ω)=tij∈S∑tij′∈S′∑max{dtij′−dtij+γ,0}
- 其中, γ > 0 \gamma > 0 γ>0是超参数,
- S ′ = { t i ′ j k ∣ e i ′ ∈ E \ e i } ⏟ replace head entity ∪ { t i j ′ k ∣ e j ′ ∈ E \ e j } ⏟ replace tail entity S^{\prime}=\underbrace{\left\{t_{i^{\prime} j}^{k} \mid e_{i}^{\prime} \in \mathcal{E} \backslash e_{i}\right\}}_{\text {replace head entity }} \cup \underbrace{\left\{t_{i j^{\prime}}^{k} \mid e_{j}^{\prime} \in \mathcal{E} \backslash e_{j}\right\}}_{\text {replace tail entity }} S′=replace head entity {ti′jk∣ei′∈E\ei}∪replace tail entity {tij′k∣ej′∈E\ej}
2.4 解码器
作者使用ConvKB作为一个解码器。卷积层的目的是分析每个维度上的三重 t i j k t_{i j}^{k} tijk的全局嵌入特性,并概括模型中的过渡特性.
多特征图的分数函数写成:
f ( t i j k ) = ( ∥ m = 1 Ω ReLU ( [ h ⃗ i , g ⃗ k , h ⃗ j ] ∗ ω m ) ) . W f\left(t_{i j}^{k}\right)=\left(\|_{m=1}^{\Omega} \operatorname{ReLU}\left(\left[\vec{h}_{i}, \vec{g}_{k}, \vec{h}_{j}\right] * \omega^{m}\right)\right) . \mathbf{W} f(tijk)=(∥m=1ΩReLU([hi,gk,hj]∗ωm)).W
- 其中, ω m \omega^{m} ωm是第 m m m个卷积核, ∗ * ∗是卷积操作。 W ∈ R Ω k × 1 \mathbf{W} \in \mathbb{R}^{\Omega k \times 1} W∈RΩk×1是线性变换来计算三元组最终分数。
最后模型被训练的损失函数为:
L = ∑ t i j k ∈ { S ∪ S ′ } log ( 1 + exp ( l t i j k . f ( t i j k ) ) ) + λ 2 ∥ W ∥ 2 2 where l t i j k = { 1 for t i j k ∈ S − 1 for t i j k ∈ S ′ \begin{array}{l}\mathcal{L}=\sum_{t_{i j}^{k} \in\left\{S \cup S^{\prime}\right\}} \log \left(1+\exp \left(l_{t_{i j}^{k} . f}\left(t_{i j}^{k}\right)\right)\right)+\frac{\lambda}{2}\|\mathbf{W}\|_{2}^{2} \\ \text { where } l_{t_{i j}^{k}}=\left\{\begin{array}{ll}1 & \text { for } t_{i j}^{k} \in S \\ -1 & \text { for } t_{i j}^{k} \in S^{\prime}\end{array}\right.\end{array} L=∑tijk∈{S∪S′}log(1+exp(ltijk.f(tijk)))+2λ∥W∥22 where ltijk={1−1 for tijk∈S for tijk∈S′
3 实验
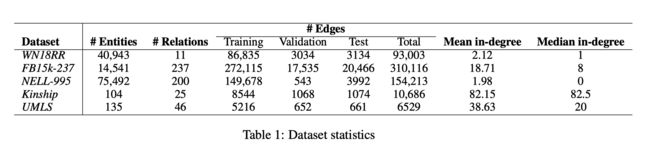
3.1 数据集
3.2 训练协议
TransE产生的实体和关系嵌入(Bordes等,2013; Nguyen等,2018)用于初始化我们的嵌入。(用transE作为初始化嵌入,这个模型越来越有取巧的嫌疑了)
作者遵循两步训练过程:
- 即我们首先训练广义GAT以编码有关图实体和关系的信息,
- 然后训练诸如ConvKB(Nguyen等人,2018)的解码器模型以执行关系预测任务。
3.3 评估标准
这明明是链接预测,咋整个关系预测,我这里怀疑作者是否有好好的研究知识表示相关内容
3.4 实验结果
这图根本看不出来啥呀。
pagerank
这个接触过,不知道作用,
消融实验
这里作者对于两个消融实验也不多描述清楚一下:
- -PG这个不清楚是移除了啥,那个辅助关系本来也没搞懂。但这个我觉得本来传播模型的时候就带入了多跳传输。
- -Relation,这个应该是直接采用GAT的方式,没有考虑关系