datawhale基于高斯分布的朴素贝叶斯分类器及聚类问题
反思与总结:
(1)朴素贝叶斯的分类模型公式P(c/x)=P©P(x/c)/P(x),其中P©为先验概率,P(x/c)为条件概率,P(x)对于任何类别来说都相同,因此只需比较P©P(x/c)即可,例子中提到的鸢尾花每个类别个数相同,即每个类别P©都相同,只需比较条件概率即可,例子中假定鸢尾花每个特征服从高斯概率分布,通过公式计算出不同类别下每个样本的条件概率,比较哪个类别的概率大,就是属于哪个类别。
(2)KMeans解决鸢尾花分类问题时,要注意类别数目的选取,DBSCAN聚类要注意两个eps与min_samples两个参数的选择,可以多尝试几次,例子中KMeans要比DBSCAN得分要高,但很多问题是DBSCAN要优于KMeans。
(3)对数据进行标准化缩放后再次进行贝叶斯分类,发现得分从0.96变为1.0,还是有所增长,看来数据特征的构造与提取是上分的一个方向,今后还将对模型选择进行评估,看得分能否再提高,以下是本次打卡的代码部分。
1.调用朴素贝叶斯模型解决鸢尾花分类问题计算得分
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2)
std_x = StandardScaler()
X_train = std_x.fit_transform(X_train)
X_test = std_x.transform(X_test)
clf = GaussianNB().fit(X_train, y_train.ravel())
print ("Classifier Score:", clf.score(X_test, y_test))
Classifier Score: 1.0
2.基于高斯分布构造朴素贝叶斯分类器
import math
class NaiveBayes:
def __init__(self):
self.model = None
@staticmethod
def mean(X):#求解每个类别每个特征的期望
avg = 0.0
avg = sum(X) / float(len(X))
return avg
def stdev(self, X):#求每个类别每个特征的方差
res = 0.0
avg = self.mean(X)
res = math.sqrt(sum([pow(x - avg, 2) for x in X]) / float(len(X)))
return res
def gaussian_probability(self, x, mean, stdev):#计算高斯概率分布下每个数据对应的概率值
res = 0.0
exponent = math.exp(-(math.pow(x - mean, 2) / (2 * math.pow(stdev, 2))))
res = (1 / (math.sqrt(2 * math.pi) * stdev)) * exponent
return res
def summarize(self, train_data):#计算每个特征期望和方差放入列表中
summaries = [0.0, 0.0]
summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]
return summaries
def fit(self, X, y):#计算每个类别对应特征的期望和方差,并放入字典中
labels = list(set(y))
data = {label: [] for label in labels}
for f, label in zip(X, y):
data[label].append(f)
self.model = {label: self.summarize(value) for label, value in data.items()}
return 'gaussianNB train done!'
def calculate_probabilities(self, input_data):#计算数据对应类别的概率
probabilities = {}
for label, value in self.model.items():
probabilities[label] = 1
for i in range(len(value)):
mean, stdev = value[i]
probabilities[label] *= self.gaussian_probability(
input_data[i], mean, stdev)
return probabilities
def predict(self, X_test): #得出概率较高的类别
label = sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1])[-1][0]
return label
def score(self, X_test, y_test):#计算测试集精确度
right = 0
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right += 1
return right / float(len(X_test))
3.调用分类器训练模型计算得分
model = NaiveBayes()
model.fit(X_train, y_train)
model.score(X_test, y_test)
1.0
4.KMeans聚类解决鸢尾花分类问题
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
km2=KMeans(n_clusters=3).fit(iris.data)
5.sepal length和sepal width聚类图像展示
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
d0=np.where(km2.labels_ == 0)
d1=np.where(km2.labels_ == 1)
#d2=np.where(km2.labels_ == 2)
km2.labels_[d0]=1
km2.labels_[d1]=0
x0 = iris.data[km2.labels_ == 0]
x1 = iris.data[km2.labels_ == 1]
x2 = iris.data[km2.labels_ == 2]
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
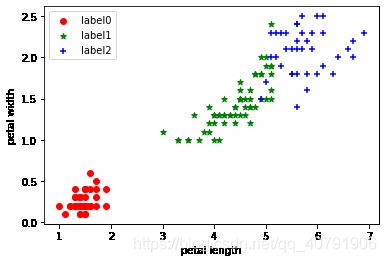
6.pental length和pental width聚类图像展示
plt.scatter(x0[:, 2], x0[:, 3], c="red", marker='o', label='label0')
plt.scatter(x1[:, 2], x1[:, 3], c="green", marker='*', label='label1')
plt.scatter(x2[:, 2], x2[:, 3], c="blue", marker='+', label='label2')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
7.sepal length和sepal width真实分类图像展示
x0 = iris.data[iris.target == 0]
x1 = iris.data[iris.target == 1]
x2 = iris.data[iris.target == 2]
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
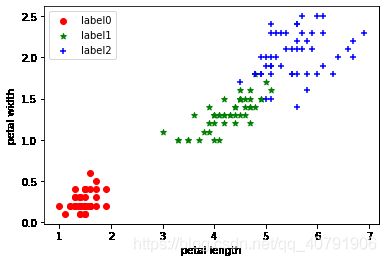
8.pental length和pental width真实分类图像展示
x0 = iris.data[iris.target == 0]
x1 = iris.data[iris.target == 1]
x2 = iris.data[iris.target == 2]
plt.scatter(x0[:, 2], x0[:, 3], c="red", marker='o', label='label0')
plt.scatter(x1[:, 2], x1[:, 3], c="green", marker='*', label='label1')
plt.scatter(x2[:, 2], x2[:, 3], c="blue", marker='+', label='label2')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
9.计算KMeans聚类结果精度得分
c=[]
for i in range (len(iris.target)):
if km2.labels_[i]==iris.target[i]:
c.append(1)
np.sum(c)/len(iris.target)
0.8933333333333333
10.DBSCAN聚类解决鸢尾花分类问题
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.5, min_samples=12)
dbscan.fit(iris.data)
label_pred = dbscan.labels_
x0 = iris.data[label_pred == 0]
x1 = iris.data[label_pred == 1]
x2 = iris.data[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
11.petal length petal width聚类图像展示
x0 = iris.data[label_pred == 0]
x1 = iris.data[label_pred == 1]
x2 = iris.data[label_pred == 2]
plt.scatter(x0[:, 2], x0[:, 3], c="red", marker='o', label='label0')
plt.scatter(x1[:, 2], x1[:, 3], c="green", marker='*', label='label1')
plt.scatter(x2[:, 2], x2[:, 3], c="blue", marker='+', label='label2')
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(loc=2)
plt.show()
12.DBSCAN聚类结果精度
c=[]
for i in range (len(iris.target)):
if label_pred[i]==iris.target[i]:
c.append(1)
np.sum(c)/len(iris.target)
0.7