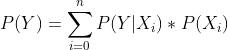机器学习——朴素贝叶斯原理(知识基础)
-
原理
正向概率:已知袋子里有m个黑球,n个白球,摸一个球摸出黑球的概率是多大?
逆向概率:一个未知的袋子里有一些黑球和白球,随机摸出一个或者好几个球,观察摸出的球可以对袋子里的黑球白球的比例做出什么样的推测?
朴素贝叶斯要解决的问题就是如何求逆向概率
一个更形象的例子:
已知学校中的60%的人是男生,40%的人是女生,其中男生总是穿着长裤,女生则一半穿长裤,一半穿裙子。
正向概率:随机选择一个男生或者女生,她/他穿长裤/长裙的概率是多少?
逆向概率:迎面走来一个穿长裤的人,不能确定ta的性别,你能推断出ta是男生/女生的概率是多少?
条件概率的公式为P(X|Y),表示在已知Y情况下X发生的概率。所以对于正向概率,即我们已知男生女生,只需根据题目中的概率直接就可以计算穿长裤和穿裙子的概率:
- P(穿长裤|男生)=1
- P(穿裙子|男生)=0
- P(穿长裤|女生)=0.5
- P(穿裙子|女生)=0.5
对于逆向概率,我们想求的是,走过来的穿长裤的这个人ta是男生和女生的概率:
P(男生|穿长裤)和P(女生|穿长裤),但是并不好计算
贝叶斯公式有一个推导式:P(X|Y)=P(XY)/P(Y),即在Y的情况下发生X的概率等于同时发生X和Y的概率再除以发生Y的概率。所以这个问题可以转化为:
P(男生并且穿长裤)/P(穿长裤)和 P(女生并且穿长裤)/P(穿长裤)
假设总人数为N,那么穿长裤的总人数为:N*0.6*1+N*0.4*0.5,
- 男生并且穿长裤的人数=N*P(男生)*1
- 女生并且穿长裤的人数=N*P(女生)*0.5
所以,P(男生并且穿长裤)/P(穿长裤)=0.6*N/0.8*N=0.75
P(女生并且穿长裤)/P(穿长裤)=0.2*N/0.8*N=0.25
另外,我们可以将P(XY)给分解成P(Y|X)*P(X),也就是:
P(男生并且穿长裤)=P(穿长裤|男生)*P(男生)
因此,再求逆向概率时,得到了一个神奇的变换:
即: P(男生|穿长裤)=P(穿长裤|男生)*P(男生)/P(穿长裤)
这也就是贝叶斯公式的作用,我们遇到一个不好直接求的条件概率,但是我们可以计算反过来的条件概率,变换之后就很容易计算
在上面式子中穿长裤的只有男生女生两类:P(穿长裤)=P(穿长裤|男生)*P(男生)+P(穿长裤|女生)*P(女生)可以得到公式:
接下来考虑一个更为复杂也更为实际的情况,如何判断一封邮件是一封垃圾邮件?也就是说我们需求出P(垃圾邮件|邮件内容)(已知邮件内容求是垃圾邮件的概率),这个显然也不好求,使用朴素贝叶斯公式:
P(垃圾邮件|邮件内容)
=P(垃圾邮件和邮件内容)/P(邮件内容)
=P(邮件内容|垃圾邮件)*P(垃圾邮件)/P(邮件内容)
P(邮件内容|垃圾邮件)是在垃圾邮件中出现这些邮件内容的概率是多少
P(垃圾邮件)是垃圾邮件的概率
其中最后的P(邮件内容)对结果并没有影响,因为P(正常邮件|邮件内容)的分母也有此项,可以认为是一个常数,也就是说P(垃圾邮件|邮件内容)正相关于P(邮件内容|垃圾邮件)*P(垃圾邮件)
所以问题可以转换为:
P(邮件内容|垃圾邮件)*P(垃圾邮件)
P(垃圾邮件)
这一部分的概率是称为先验概率,是指根据以往经验和分析得到的概率,比如P(硬币正面朝上)=0.5,可以认为是根据大数定律,频率可以趋近于概率,也就是说我们找足够多的数据样本(10万 封邮件或者更多),那么其中垃圾邮件出现的频率(6万次)就可以是认为是P(垃圾邮件)=0.6的概率,这一部分的概率是根据一个庞大的先验集(数据集)来确定的
P(邮件内容|垃圾邮件)
另一部分就是垃圾邮件中邮件内容出现的概率了,显然是不可能计算整封邮件的内容,由于邮件内容是由词ABCD.....组成的,所以可以将概率拆开,正常情况下一封邮件的每个词之间都有前后文关联的,例“我喜欢逛街”和“逛我街欢喜”是两个不同的语义,这个概率应该被写作:
P(邮件内容|垃圾邮件)=P(A|垃圾邮件)*P(B|A,垃圾邮件)*P(C|A,B垃圾邮件).....
也就是说每一个词出现的概率都需要计算前面的词已经出现过的概率,这个计算量是非常大的。朴素贝叶斯的思想就体现在这里,假设每个特征之间是相互独立的,“我喜欢逛街”和“逛我街欢喜”,只要是这五个字的排列组合就都认为是同一种情况,没有区别,这大大减少了计算量,也就是只计算出现词的概率,不再去计较词之间先后的关系了。
P(邮件内容|垃圾邮件)=P(A|垃圾邮件)*P(B|垃圾邮件)*P(c|垃圾邮件)....
也就是说我们只需要统计出先验集(训练集)的垃圾邮件中邮件内容的每个词出现的概率就可以了,这时会产生一个问题,如果这个词没有出现过我们该怎么做呢?
对于一个从未见过的词,在训练集中没有对应的概率值,P(x|垃圾邮件)=0,这显然不合适,因为我们需要计算P(邮件内容|垃圾邮件)的时候需要把每个词的 概率相乘,某一项为0的话就会使乘积为零,这显然是不合适的,所以我们要想办法不让他为0.
这个错误的造成是由于训练量不足,会令分类器质量大大降低。为了解决这个问题,我们引入Laplace校准(拉普拉斯平滑),它的思想就是对每个类别下所有划分的计数+1,这样当训练样本集数量充分大是,并 不会对结果产生影响,并且解决了上述概率为0(它趋近于0,因为分母极大,而分子为1)的尴尬局面。
举个例子,如果垃圾邮件中有2个“售”,3个“买”,.....,现在的进来的邮件内容是“购”,在原数据集中并没有出现,那么对于垃圾邮件中的每一个词的数量+1,变为3个“售”,4个“买”,1个“购”....这样每个类都加了一个,使分子不再为0.
Dataset
我们使用的是
Email数据集:已经处理好的邮件分类,判断垃圾邮件还是正常邮件
搜狗数据集:搜狗新闻数据集,判断属于哪一类
python main.py --emailpython main.py --sougou
在终端输入这两个就可以查看分类效果了
由于这两个数据集不是很大,所以直接放到文件夹里,一般情况下是放到release里面