树与二叉树的存储结构，二叉树的多种遍历实现

树

- 树不可以为空

- 子树互不相交

- 除了根结点之外，每个结点有且只有一个父结点

- 一棵n个结点的树有n-1条边

- 结点的度：结点的子树个数

树的存储结构

- 树没有顺序存储结构（没法表示结点之间的关系）

- 静态链式存储（双亲表示法、孩子表示法、双亲孩子表示法）

- 孩子链表示法（结点里是下标而不是数据）

---

---

二叉树

- 可以为空，不是树的一种特殊情况

- 有两个孩子的结点总数  = 叶子结点总数 - 1

（边数的两种算法：）

- 二叉树第i层的最大结点数为：

- 深度为k的二叉树最大结点总数为：

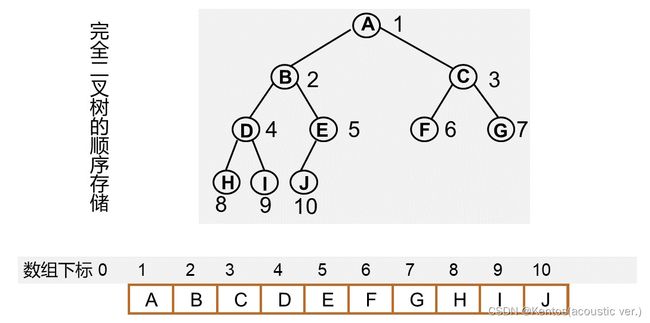
顺序存储

完全二叉树或满二叉树中结点的序号可以唯一地反映出结点之间的逻辑关系

-非根结点的父结点的序号为[i/2]

-序号为i的结点的左孩子的结点的序号为2i（若2i<=n，则没有左孩子）

-序号为i的结点的右孩子的结点的序号为2i+1（若2i+1<=n，则没有左孩子）

-一般二叉树可以通过增添一些不存在的空结点使其成为完全二叉树（浪费空间）

---

 链表

存储结点信息以及指向左右孩子的指针

数据结构定义

//二叉树定义
typedef int ElementType; //假设结点数据是整数
//也可以用 typedef char ElementType; 那么结点数据为char型
typedef struct TNode *Position;
typedef Position BinTree; //二叉树类型
struct TNode{ //树结点定义
    ElementType Data; //结点数据
    BinTree Left; //指向左子树
    BinTree Right; //指向右子树
};

二叉树的创建

void CreatBinTree (BinTree &BT) //先序遍历过程创建二叉树
{
    ElementType c;
    printf("输入一个结点整数，空结点输入-1:");
    scanf("%d",&c);
    if (c==NoInfo) BT=NULL; //#define NoInfo -1 表示没有结点
    else {
        BT=(Position)malloc(sizeof(TNode)); //结点申请
        BT->Data=c;
        CreatBinTree(BT->Left);
        CreatBinTree(BT->Right);
    }
}

二叉树的遍历

前序（根）遍历的递归算法

//此处假设对BT结点的访问就是打印数据
void PreorderTraversal(BinTree BT)
{
    if(BT) {
        printf("%-4d", BT->Data); //先访问根结点
        PreorderTraversal(BT->Left); //再访问左子树
        PreorderTraversal(BT->Right); //最后访问右子树
    }
}

//先序遍历输出二叉树叶子结点
void PreorderPrintLeaves(BinTree BT)
{
    if(BT) {
        if (!BT->Left && !BT->Right) //如果BT结点是叶子结点
            printf("%-3d", BT->Data);
        PreorderPrintLeaves (BT->Left);
        PreorderPrintLeaves (BT->Right);
    }
}

中序（根）遍历和后序（根）遍历只是调整了下访问的顺序

void InorderTraversal(BinTree BT) //中序（根）遍历的递归算法
{
    if(BT) {
        InorderTraversal(BT->Left); //先访问左子树
        printf("%-4d", BT->Data); //再访问根结点
        InorderTraversal(BT->Right); //最后访问右子树
    }
}

void PostorderTraversal(BinTree BT) //后序（根）遍历的递归算法
{
    if(BT) {
        PostorderTraversal(BT->Left); //先访问左子树
        PostorderTraversal(BT->Right); //再访问右子树
        printf("%-4d", BT->Data); //最后访问根结点
    }
}

非递归算法——栈

- 栈的顺序存储（一维数组）

//栈的数据结构声明
struct SNode {
    BinTree *SData; //存储元素的数组，类型为BinTree，是指向二叉树结点的指针
    int Top; //栈顶指针，存的是栈顶元素的下标
    int MaxSize; //堆栈最大容量
};
typedef struct SNode *Stack;

//栈的基本操作函数定义
Stack CreateStack(int MaxSize) //栈的创建
{
    Stack S = (Stack)malloc(sizeof(struct SNode));
    S->SData = (Position*)malloc(MaxSize *sizeof(TNode));
    S->Top = -1;
    S->MaxSize = MaxSize;
    return S;
}

bool IsFull(Stack S) //判断栈是否已满
{
    return (S->Top == S->MaxSize-1);
}

bool Push(Stack S, BinTree X) //入栈
{
    if (IsFull(S)) {
        printf("堆栈满");
        return false;
    }
    else {
        S->SData[++(S->Top)] = X; //栈顶元素下标+1
        return true;
    }
}

bool IsEmpty(Stack S) //判断栈是否已空
{
    return (S->Top == -1);
}

BinTree Pop(Stack S) //栈顶元素出栈
{
    if (IsEmpty(S)) {
        printf("堆栈空，无元素\n\n");
        return ERROR; //#define ERROR NULL
    }
    else
        return (S->SData[(S->Top)--]); //栈顶元素下标-1
}

- 栈的链式存储

//二叉树定义
typedef int ElementType;
typedef struct TNode *BinTree;
struct TNode{ //树结点定义
    ElementType Data; //结点数据
    BinTree Left; //指向左子树
    BinTree Right; //指向右子树
};
//栈的链式存储数据结构定义
typedef struct SNode *PtrToSNode;
struct SNode{
    BinTree Data; //将树的结点指针作为栈的元素
    PtrToSNode Next;
    int MaxSize;
};

//栈的基本操作函数
Stack CreateStack(int maxsize) //构建一个堆栈的头结点，返回该结点指针
{
    Stack S;
    S = (Stack)malloc(sizeof(struct SNode));
    S->Next = NULL;
    S->MaxSize = maxsize;
    return S;
}
bool IsSEmpty (Stack S) //判断堆栈S是否为空
{
    return ( S->Next == NULL );
}

bool Push(Stack S, BinTree BT) //将元素X压入堆栈S
{
    PtrToSNode TmpCell;
    TmpCell = (PtrToSNode)malloc(sizeof(struct SNode));
    TmpCell->Data = BT;
    TmpCell->Next = S->Next;
    S->Next = TmpCell;
    return true;
}

BinTree Pop(Stack S) //删除并返回堆栈S的栈顶元素
{
    PtrToSNode FirstCell;
    BinTree TopElem;
    TopElem = FirstCell->Data;
    if(IsSEmpty(S)) {
        printf("堆栈空，无元素\n\n");
        return NULL;
    }
    else {
        FirstCell = S->Next;
        TopElem = FirstCell->Data;
        S->Next = FirstCell->Next;
        free(FirstCell);
        return TopElem;
    }
}

前序（根）遍历的非递归算法

void PreOrder_NR(BinTree BT)
{
    BinTree T = BT;
    Stack S = CreateStack(30);
    while (T || !IsEmpty(S)) {
        while (T != NULL) { //一直向左并将沿途结点压入堆栈
            printf("%-3d", T->Data); //访问（根）结点
            Push(S,T); //将左子树存储到栈中
            T = T->Left; //遍历左子树
        }
        if (!IsEmpty(S)) {
            T = Pop(S); //结点弹出堆栈
            T = T->Right; //遍历右子树
        }
    }
}

中序遍历的非递归算法

void Inorder_NR(BinTree BT)
{
    BinTree T=BT; //从根结点出发
    Stack S = CreateStack(30); //创建空堆栈S，元素类型为BinTree
    while(T || !IsEmpty(S)) {
        while(T) {
            Push(S,T);
            T = T->Left; //一直向左并将沿途结点压入堆栈
        }
        if (!IsEmpty(S)) {
            T = Pop(S); //结点弹出堆栈
            printf("%-3d", T->Data); //(访问)打印结点
            T = T->Right; //转向右子树
        }
    }
}

层序遍历——队列

队列的声明

//队列的链式存储结构定义
//队列中的结点定义
typedef struct Node *PtrToNode;
struct Node {
    BinTree Data; //每个元素是一个指向二叉树结点的指针
    PtrToNode Next;
};
//队列定义
struct QNode {
    PtrToNode Front, Rear; //队列的头、尾指针
    int MaxSize; //队列最大容量
};
typedef struct QNode *Queue;

//队列的基本操作函数
Queue CreateQueue(int maxsize)
{
    Queue Q;
    Q = (Queue)malloc(sizeof(struct QNode));
    Q->Front = NULL;
    Q->Rear = NULL;
    Q->MaxSize=maxsize; //Q->MaxSize 没有实际意义，只为与抽象数据类型定义一致
    return Q;
}

bool IsEmpty(Queue Q)
{
    return (Q->Front == NULL);
}

bool AddQ(Queue Q, BinTree X) //入队
{
    PtrToNode RearCell;
    RearCell = (PtrToNode)malloc(sizeof(struct Node)); //结点申请
    RearCell->Data = X;
    RearCell->Next = NULL; //Rear是最后一个元素
    if (IsEmpty(Q))
        Q->Front = RearCell; //队列中没有其他元素
    else
        Q->Rear->Next = RearCell; //直接在原来的队尾结点后边添加
    Q->Rear = RearCell; //新的队尾
    return true;
}

BinTree DeleteQ(Queue Q) //出队
{
    PtrToNode FrontCell; //临时存储队头结点
    BinTree FrontElem; //队头结点存储的数据，类型为二叉树结点
    if (IsEmpty(Q)) {
        printf("队列空");
        return ERROR;
    }
    else {
        FrontCell = Q->Front;  //均为PtrToNode型指针
        if (Q->Front == Q->Rear) //若队列只有一个元素
            Q->Front = Q->Rear = NULL; //删除后队列置为空
        else
            Q->Front = Q->Front->Next; //原队头结点的下一个结点作为新的队头结点
        FrontElem = FrontCell->Data;
        free(FrontCell); //释放被删除的结点（原队头结点）
        return FrontElem; //返回被删除的结点，类型为二叉树结点
    }
}

由上至下逐层遍历，在同一层中从左至右顺序访问每个结点

void LevelorderTraversal(BinTree BT)
{
    Queue Q;
    BinTree T;
    if (!BT)
        return; //若是空树则直接返回
    Q = CreateQueue(50); //创建空队列Q，返回队头结点
    AddQ(Q, BT); //头结点入队
    while (!IsEmpty(Q)) {
        T = DeleteQ(Q);
        printf("%-3d", T->Data); //访问取出队列的结点
        if (T->Left) //左子树不为空
            AddQ(Q,T->Left); //访问取出左孩子
        if (T->Right) //右子树不为空
            AddQ(Q,T->Right); //访问取出右孩子
    }
}

二叉树的其他操作

交换左右子树

Position exchange(BinTree BT)
{
    BinTree tmp; //临时变量，类型为二叉树结点
    if(BT) { //先交换根结点的左右子树
        tmp = BT->Right;
        BT->Right = BT->Left;
        BT->Left = tmp;
        exchange(BT->Left); //递归交换左子树的左右子树
        exchange(BT->Right); //递归交换右子树的左右子树
    }
    return BT;
}

求二叉树的高度（递归实现）

int GetHeight(BinTree BT)
{
    int HL, HR, MaxH;
    if(BT) {
        HL = GetHeight(BT->Left); //递归求左子树的高度
        HR = GetHeight(BT->Right); //递归求右子树的高度
        MaxH = HL > HR ? HL : HR; //取左右子树较大的高度
        return ( MaxH + 1 ); //返回树的高度（根结点++）
    }
    else
        return 0; //空树高度为0
}

对以上遍历的简单测试

int main() {
    BinTree BT;
    printf("创建二叉树，请输入二叉扩展树先序序列:\n\n");
    CreatBinTree(BT);
    printf("\n\n");

    printf("前序遍历结果:");
    PreorderTraversal(BT); printf("\n\n");
    printf("二叉树的叶子结点为:");
    PreorderPrintLeaves(BT);
    printf("\n\n");

    printf("中序遍历结果:");
    InorderTraversal(BT);
    printf("\n\n");
    printf("后序遍历结果:");
    PostorderTraversal(BT);
    printf("\n\n");

    printf("非递归前序结果:");
    PreOrder_NR(BT);
    printf("\n\n");
    printf("非递归中序结果:");
    Inorder_NR(BT);
    printf("\n\n");

    printf("非递归层序遍历结果:");
    LevelorderTraversal(BT);
    printf("\n\n");

    printf("二叉树的高度为:");
    printf("%d\n\n",GetHeight(BT));

    printf("交换左右子树后，先序遍历结果:");
    exchange(BT);
    PreorderTraversal(BT);
    printf("\n\n");

    return 0;
}

练习题：

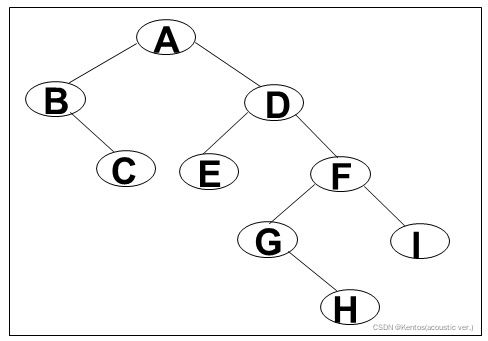
已知一棵二叉树的前序遍历序列为A B C D E F G H I，中序遍历序列为B C A E D G H F I，确定该二叉树并写出后序遍历序列。

前序遍历第一个访问的一定是根结点，故这棵二叉树的根结点是A；

中序遍历中先访问左子树然后是根结点和右子树，找到根结点A，则左边的BC在左子树上，右边的EDGHF在右子树上；

再看左子树，先访问的B，则B为左子树的根结点，中序遍历中C在B右边，故C在B的右子树上；

同样的方法可以得出右子树的根结点为D，D的左孩子有E，右孩子有FGHI；

...

最后得到此二叉树如下图所示，后序遍历的结果为：C B E H G I F D A