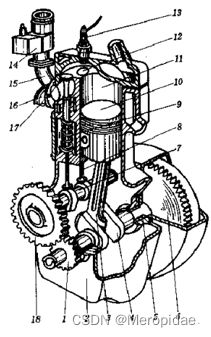
matlab单缸内燃机设计
已知活塞的行程为216mm,进气门控制杆的行程为13mm。
1.设计曲柄滑块机构,分析所设计机构的最小传动角,若机构运动时存在问题,请提出解决方案。
2.取基圆半径为30mm,自拟进气门控制杆运动规律,试设计凸轮轮廓曲线。
设计分析问题,针对内燃机机构本身的特点展开分析,可进行拓展。采用解析法进行matlab编程。
分析内燃机结构,核心分为两部分,凸轮机构和四杆机构
程序基于这两部分来设计;第一部分是对四杆机构的设计
设计阶段:
选用较为简单的对心曲柄滑块机构,分析程序参数设置如下:
曲柄长度r1=6.5mm;
连杆长度r2=25.5mm;
曲柄/连杆=0.255;
滑块(活塞)位移距离r3=13mm;
r1=6.5; %曲柄 单位mm
r2=25.5%连杆
x11=1:720;
for i=1:720
x1(i)=i*pi/180;%曲柄角度
%sin(x2(i))=-r1/r2*sin(x1(i));
x2(i)=asin(-r1/r2*sin(x1(i)));%连杆角度
r3(i)=r1*cos(x1(i))+r2*cos(x2(i));%滑块位移长度
a(i)=90-abs(x2(i)/(pi/180))%传动角
end
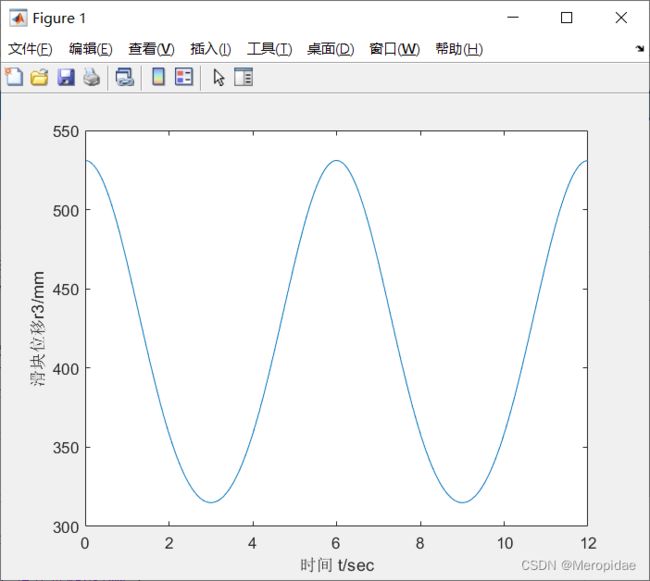
plot(x11/60,r3);
xlabel('时间 t/sec')
ylabel('滑块位移r3/mm')
figure(2);%创建第2个演示窗口
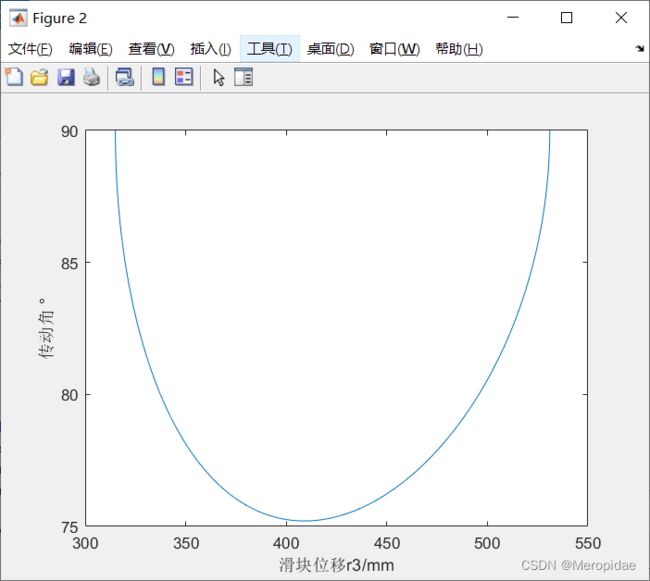
plot(r3,a);
xlabel('滑块位移r3/mm')
ylabel('传动角 °')
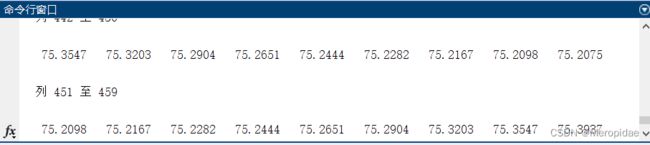
disp(a)上面为主程序,把结果也贴上来
时间与滑块位移图像
位移与传动角图像
结合窗口2图像和命令行数据可以看出最小传动角的角度约为75°
展示阶段:
clc%用来清除命令窗口的内容(确保运行正常)
clear%用来清除工作空间的内容(确保运行正常)
close all;%关闭所有的图形窗口(确保运行正常)
%以下为主程序----------------------------
l1 = 6.5;%曲柄长度做整转,一个周期的模拟。
l2 = 25.5;%连杆长度
O = [0;0];
AFir = [0;l1];%0和l1组成矩阵1*1
Angle = 0:1:360;%做整转,一圈(0°开始每次1°到360°)
A = zeros(2,size(Angle,2));%建立2行*360列的矩阵
%zeros(2,n):建立一个2*n的0矩阵;size(Angle,2):将Angle的值赋值到列,若行则用1表示
for i=1:1:size(Angle,2)%循环:i(循环变量)=表达式1(初值):表达式2(步长):表达式3(最终值)
A(:,i) = [cosd(Angle(i)),sind(Angle(i)); -sind(Angle(i)) cosd(Angle(i))]...
*((AFir - 0)*1) + O; %解析法求曲柄滑块机构的公式;...表示转下一行
end%结束循环
B(1,:) = (l2^2-abs(A(2,:)).^2).^0.5 + A(1,:); %滑块X坐标:abs表示绝对值
BVec = diff(B)/1; %滑块速度:diff(B)对B求导
%以下为绘制动图-------------------------
for i = 1:10:size(A,2)%动图绘制
cla;%表示清除坐标区域
plot([0,A(1,i)],[0,A(2,i)],'k');%绘制图形:横轴,纵轴,颜色
hold on;%持续绘制
plot([B(1,i),A(1,i)],[0,A(2,i)],'r');%k黑色,r红色,ko黑实线,k--黑虚线
plot(B(1,i),0,'ko');
plot(0,0,'ko');
plot(A(1,i),A(2,i),'ko');
plot([-1.1*l1,l1+l2],[0,0],'k--');
axis([-1.1*l1,l1+l2+1,-l1-l2,l1+l2]);%设置x轴与y轴的范围(xmin,xmax,ymin,ymax)
pause(0.1); %暂停0.1秒
end
figure(2);%创建第2个演示窗口
plot(0:0.1:35.9,BVec);%曲线图绘制
title('滑块速度图')
xlabel('时间 t/sec');
ylabel('滑块速度v mm/s');
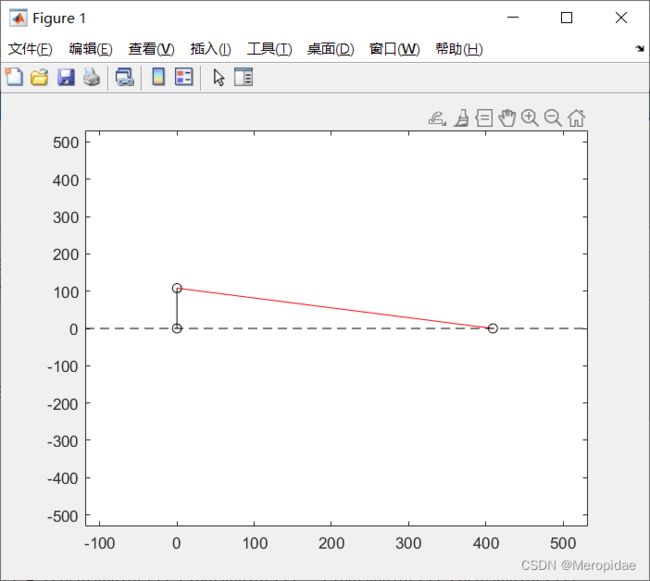
将设计结构转化为动图:
第二部分,对凸轮机构的设计
选取对心尖端移动从动件盘型凸轮机构,解析法参数设置如下:
设定推杆最大上升高度为h=13mm
凸轮基圆r0=30mm
推程运动角q=120°
远休止角qs=30°
回程运动角q1=150°
近休止角qm=60°
角速度w=12r/s
注意:程序是可以加上偏心距和滚轮的,这里只是为了简单而这样选取
%设置凸轮的基本参数
h=13;w=12;rb=30;e=0;rr=0;s0=sqrt(rb*rb-e*e);%s0最小位移(基圆)
% 偏心距e,基圆半径rb,滚轮半径rr,角速度w,推杆最大上升h
q=120*pi/180;%推程运动角为120度
qs=(120+30)*pi/180;%远休止角为150度
q1=(120+30+150)*pi/180;%回程运动角为300度
%绘制基圆
aplha=0:pi/180:2*pi;
z=rb*cos(aplha);
u=rb*sin(aplha);
%绘制偏心圆
aplha=0:pi/180:2*pi;
f=e*cos(aplha);
t=e*sin(aplha);
for i=1:1:120 %将120度按1度均分,得到各个度数上的轮廓坐标;推程
qq(i)=i*pi/180;%各点角度
s1=(h*qq(i)/q)-(h/(2*pi))*sin(2*pi*qq(i)/q);%推程位移变化值
x(i)=(s0+s1)*sin(qq(i))+e*cos(qq(i));
y(i)=(s0+s1)*cos(qq(i))-e*sin(qq(i));%理论轮廓线的坐标
a(i)=(s0+s1)*cos(qq(i))-e*sin(qq(i)); %cos(i)
b(i)=(s0+s1)*sin(qq(i))-e*cos(qq(i)); %sin(i)
xx(i)=x(i)+rr*b(i)/sqrt(a(i)*a(i)+b(i)*b(i));
yy(i)=y(i)+rr*a(i)/sqrt(a(i)*a(i)+b(i)*b(i));%实际工作轮廓线的坐标
end
for i=121:1:150%远休止
qq(i)=i*pi/180;
s2=h;%远休止推程(最大推程h)
x(i)=(s0+s2)*sin(qq(i))+e*cos(qq(i));
y(i)=(s0+s2)*cos(qq(i))-e*sin(qq(i));
a(i)=(s0+s2)*cos(qq(i))-e*sin(qq(i));
b(i)=(s0+s2)*sin(qq(i))-e*cos(qq(i));
xx(i)=x(i)+rr*b(i)/sqrt(a(i)*a(i)+b(i)*b(i));
yy(i)=y(i)+rr*a(i)/sqrt(a(i)*a(i)+b(i)*b(i));
end
for i=151:1:300%回程
qq(i)=i*pi/180;
qq1(i)=qq(i)-150*pi/180;
s3=h-h*qq1(i)/(q1-qs);%回程位移变化值
x(i)=(s0+s3)*sin(qq(i))+e*cos(qq(i));
y(i)=(s0+s3)*cos(qq(i))-e*sin(qq(i));
a(i)=(s0+s3)*cos(qq(i))-e*sin(qq(i));
b(i)=(s0+s3)*sin(qq(i))-e*cos(qq(i));
xx(i)=x(i)+rr*b(i)/sqrt(a(i)*a(i)+b(i)*b(i));
yy(i)=y(i)+rr*a(i)/sqrt(a(i)*a(i)+b(i)*b(i));
end
for i=301:1:360%近休止
qq(i)=i*pi/180;
x(i)=(s0+0)*sin(qq(i))+e*cos(qq(i));
y(i)=(s0+0)*cos(qq(i))-e*sin(qq(i));
a(i)=(s0+0)*cos(qq(i))-e*sin(qq(i));
b(i)=(s0+0)*sin(qq(i))-e*cos(qq(i));
xx(i)=x(i)+rr*b(i)/sqrt(a(i)*a(i)+b(i)*b(i));
yy(i)=y(i)+rr*a(i)/sqrt(a(i)*a(i)+b(i)*b(i));
end
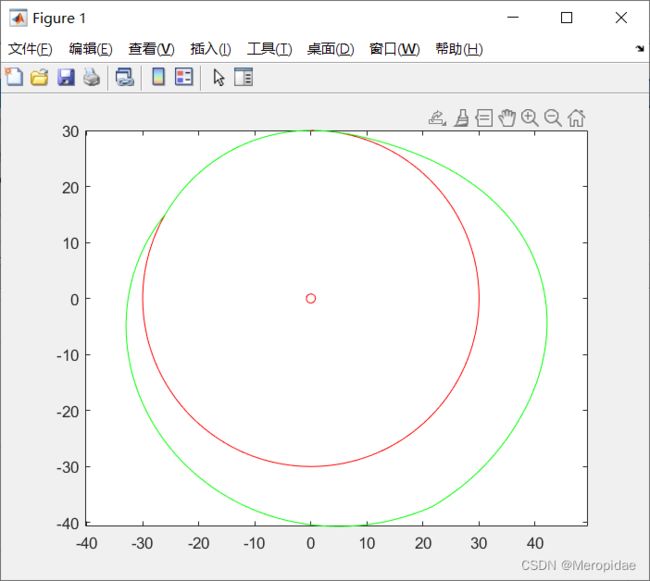
plot(0,0,'ro',z,u,'r',f,t,'b',x,y,'k',xx,yy,'g')%用plot函数绘制曲线
axis equal
hold on设计结果图像展示:
求求三连啦