You Only Learn One Representation: Unified Network for Multiple Tasks
You Only Learn One Representation: Unified Network for Multiple Tasks
- 一、引言
-
- (一)、 Explicit deep learning
- (二)、Implicit deep learning
- (三)、Knowledge modeling
- (四)、Kernel space alignment
- 二、实现细节
-
- (一)、Formulation of implicit knowledge
- (二)、Modeling implicit knowledge
- (三)、训练方式
- (四)、推理方式
- 三、实验
-
- (一)、Feature alignment for FPN
- (二)、Prediction refinement for object detection
- (三)、Canonical representation for multi-task
- (四)、 Implicit modeling with different operators
- (五)、Modeling implicit knowledge in different ways
- (六)、Analysis of implicit models
- (七)、Implicit knowledge for object detection
- 四、附录
论文地址: https://arxiv.org/abs/2105.04206
CODE: https://%20github.com/WongKinYiu/yolor
一、引言
人们通过视觉、听觉、触觉以及过去的经验来“理解”世界。人类的经验可以通过正常的学习(我们称之为外在知识)或潜意识(我们称之为内隐知识)来学习。这些通过正常学习或潜意识学到的经验会被编码并储存在大脑中。利用这些丰富的经验作为一个巨大的数据库,人类可以有效地处理数据,即使这些数据之前是看不到的。本文提出了一个统一的网络,将内隐知识和外显知识编码在一起,就像人脑可以通过正常学习和潜意识学习来学习知识一样。统一网络可以生成统一的表示,以同时服务于各种任务。可以在卷积神经网络中进行内核空间对齐、预测细化和多任务学习。结果表明,将隐式知识引入神经网络后,所有任务的性能都得到了提高。本文进一步分析了从所提出的统一网络中得到的隐式表示,它在捕捉不同任务的物理意义方面表现出了很强的能力。本文提出了一个统一的网络来整合隐性知识和显性知识,使学习到的模型包含一个通用表示,这个通用表示支持适合各种任务的子表示。下图说明了建议的统一网络架构。
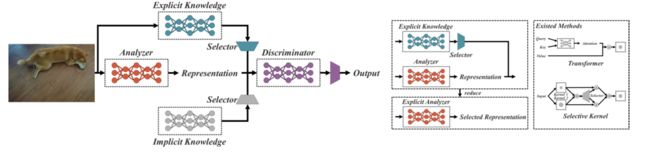
构建上述统一网络的方法是将压缩感知和深度学习相结合,这项工作的贡献概括如下:
1、提出了一个可以完成各种任务的统一网络,它通过整合内隐知识和外显知识来学习一个通用表示,通过这个通用表示可以完成各种任务。提出的网络有效地提高了模型的性能,而额外的成本非常小(小于万分之一的参数和计算量)。
2、将核空间对齐、预测精化和多任务学习引入到内隐知识学习过程中,并验证了其有效性。
3、分别讨论了用向量、神经网络和矩阵分解作为工具对隐性知识进行建模的方法,同时验证了其有效性。
4、本文证实,所提出的学习后的内隐表示可以准确地对应特定的物理特征,并且还将其以可视化的方式呈现出来。如果符合一个目标的物理意义的运算符,就可以用来整合隐性知识和显性知识,并且会产生乘数效应。
(一)、 Explicit deep learning
显式深度学习可以通过以下几种方式进行。其中,Transformer是一种方式,它主要使用查询、键或值来获取自注意。非局部网络是获取注意的另一种方式,它主要在时间和空间上提取成对的注意力。另一种常用的显式深度学习方法是根据输入数据自动选择合适的内核。
(二)、Implicit deep learning
属于内隐深度学习范畴的方法主要有内隐神经表示和深度平衡模型。前者主要是获取离散输入的参数化连续映射表示来执行不同的任务,后者是将内隐学习转化为残差形式的神经网络,并在其上进行平衡点计算。
(三)、Knowledge modeling
知识建模的方法主要包括稀疏表示和记忆网络。前者使用范例、预定义过完备或学习字典进行建模,而后者则依靠结合各种形式的嵌入形成记忆,并使记忆能够动态添加或更改。
本文认为,一个好的表现应该能够在它所属的多方面空间中找到一个适当的投影,并促进后续的客观任务取得成功。例如,如下所示,如果投影空间中的超平面能够成功地对目标类别进行分类,那将是最好的结果。在上面的例子中,我们可以取投影向量与隐式表示的内积,达到降低流形空间维数,有效完成各种任务的目的
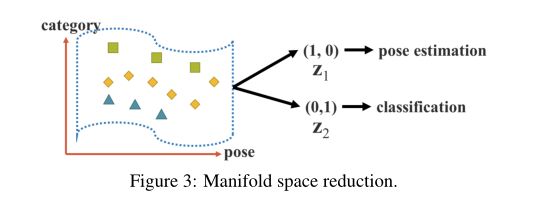
(四)、Kernel space alignment
在多任务和多头神经网络中,内核空间失调是一个常见的问题,下图说明了多任务和多头神经网络中内核空间失调的一个例子。为了解决这个问题,可以对输出特征和隐式表示进行加法和乘法运算,这样Kernel空间就可以通过平移、旋转、缩放来对齐神经网络的每个输出内核空间,

如下所示。上述操作模式可广泛应用于不同领域,如特征金字塔网络(FPN)中大对象和小对象的特征对齐,利用知识蒸馏集成大模型和小模型,以及处理零射域转移等问题。
二、实现细节
(一)、Formulation of implicit knowledge
Conventional Networks:对于常规网络训练的目标函数,我们可以用(1)表示为:

其中x为观测值,θ为神经网络的参数集合, f θ f_θ fθ表示神经网络的操作,z为误差项,y为给定任务的目标。
在传统神经网络的训练过程中,通常会最小化z使 f θ ( x ) f_θ(x) fθ(x)尽可能接近目标。这意味着期望对同一目标的不同观测结果是由 f θ f_θ fθ得到的子空间中的一个点,如下图所示。
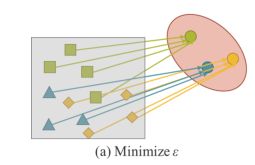
换句话说,我们期望获得的解空间只对当前任务 t i t_i ti具有区别性,而对各种潜在任务 T t i T \ t_i T ti中除 t i t_i ti以外的任务具有不变性,其中 T = t 1 , t 2 , … , t n T = {t_1, t_2,…, t_n} T=t1,t2,…,tn。
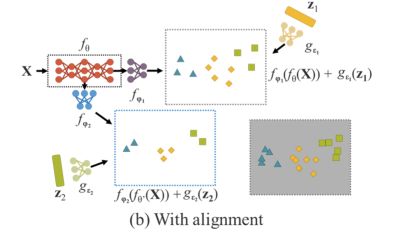
对于通用神经网络,我们希望得到的表示能够服务于所有属于T的任务。因此,我们需要在流形空间上同时找到每个任务的解成为可能,如图6 (b)所示。
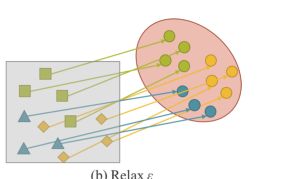
但是,由于上述要求,我们不可能用简单的数学方法,如one-hot 向量的最大值,欧氏距离的阈值来求解 t i t_i ti。为了解决这个问题,我们必须建立误差项的模型z为不同的任务寻找解决方案,如下图所示。
Unified Networks:为了训练所提出的统一网络,我们将显式和隐式知识结合起来对误差项进行建模,然后用它来指导多用途网络的训练过程。相应的训练方程为:

其中 z e x z_{ex} zex和 z i m z_{im} zim分别是将观察值x和潜码z. g φ g_φ gφ的显式误差和隐式误差建模为任务特定操作,用于从显式知识和隐式知识中组合或选择信息。
已有一些方法可以将显式知识积分到 f θ f_{θ} fθ中,因此:
![]()
*表示可以组合 f θ f_θ fθ和 g φ g_φ gφ的一些可能的算子。在这项工作中,将使用加法、乘法和拼接。
(二)、Modeling implicit knowledge
提出的隐性知识可以通过以下几种方式建模:
V ector / Matrix / Tensor:
![]()
直接使用向量z作为隐性知识的先验,直接作为隐性表示。此时,必须假设每个维度彼此独立。
Neural Network:
![]()
用向量z作为隐式知识的先验,然后用权值矩阵W进行线性组合或非线性化,然后成为隐式表示。这时,必须假定每个维度是相互依赖的。也可以使用更复杂的神经网络来生成隐式表示。或者使用马尔可夫链来模拟不同任务之间隐式表示的相关性。
Matrix Factorization:![]()
使用多个向量作为隐性知识的先验,这些隐性先验基Z和系数c将形成隐性表示。还可以进一步对c进行稀疏约束,并将其转化为稀疏表示形式。此外,还可以对Z和c施加非负约束,将它们转化为非负矩阵分解(NMF)形式。
(三)、训练方式
假设我们的模型在开始时没有任何先验的隐性知识,也就是说,它对显式表示 f θ ( x ) f_θ(x) fθ(x)没有任何影响。当组合算子 ∗ ∈ { a d d i t i o n , c o n c a t e n a t i o n } *∈\{addition, concatenation\} ∗∈{addition,concatenation},初始隐式先验 z N ( 0 , σ ) z ~ N(0, σ) z N(0,σ),而当精算符*为乘法, z N ( 1 , σ ) z ~ N(1, σ) z N(1,σ)。σ是一个非常小的值,接近于零。对于z和φ,在训练过程中都采用反向传播算法进行训练。
(四)、推理方式
由于隐式知识与x无关,所以无论隐式模型 g φ g_φ gφ有多复杂,都可以在推理阶段执行之前将其简化为一组常数张量。换句话说,隐式信息的形成对我们算法的计算复杂度几乎没有影响。另外,当上述算子为乘法时,如果后续层为卷积层,则使用下面方式进行积分。
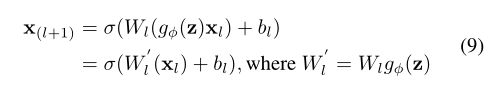
当遇到加法运算符时,如果前一层是卷积层且没有激活函数,则使用(10)进行积分。

三、实验
在实验设计中,选择将隐式知识应用于三个方面,包括1个FPN的特征对齐,2个预测精化,3个单模型的多任务学习。多任务学习包括1个目标检测,2个多标签图像分类,3个特征嵌入。我们在实验中选择YOLOv4CSP作为基线模型,并在下图箭头所指的位置向模型中引入隐性知识。所有的训练超参数都与scaledyolo4的默认设置进行比较。
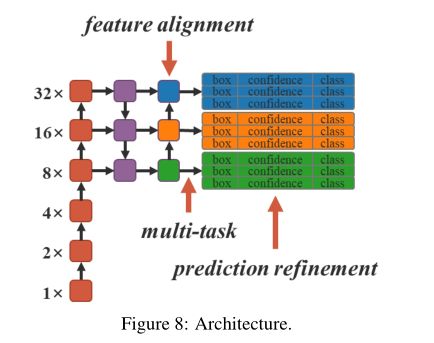
(一)、Feature alignment for FPN
在每个FPN的特征图中加入隐式表示进行特征对齐,相应的实验结果如下表所示。从表所示的这些结果中我们可以说:在使用隐式表示进行特征空间对齐后,包括 A P S AP_S APS、 A P M AP_M APM和 A P L AP_L APL在内的所有性能都提高了约0.5%,这是非常显著的改进。

(二)、Prediction refinement for object detection
隐式表示被添加到YOLO输出层,用于预测细化。如下表所示,几乎所有的指标得分都得到了提高。图9显示了隐式表示的引入如何影响检测结果。在对象检测的情况下,即使我们不为隐式表示提供任何先验知识,所提出的学习机制仍然可以自动学习每个锚点的(x, y)、(w, h)、(obj)和(classes)模式。

(三)、Canonical representation for multi-task
当要训练一个可以同时被多个任务共享的模型时,由于必须执行损失函数的联合优化过程,在执行过程中经常会有多方相互拉。上述情况会导致最终的整体性能不如单独训练多个模型再进行集成。为了解决上述问题,提出训练一个多任务的规范表示。通过向每个任务分支引入隐式表示来增强表示能力,下表列出了隐式表示的影响。如所示的数据,在不引入隐式表示的情况下,多任务训练后,部分指标得分提高,部分下降。将隐式表示引入联合检测与分类(joint detection and classification, JDC)后,在+ iJDC对应的模型类别中,我们可以清楚地看到,整体指标得分有了明显的提高,并且超过了单任务训练模型的表现。与不引入隐式表示时相比,模型在中型对象和大型对象上的性能也分别提高了0.3%和0.7%。在联合检测与嵌入(JDE)实验中,由于特征对齐所隐含的隐式表示特性,提高指标得分的效果更为显著。

(四)、 Implicit modeling with different operators
下表显示了使用图10所示的不同运算符组合显式表示和隐式表示的实验结果。在特征对齐实验的隐式知识中,我们看到加法和拼接都能提高性能,而乘法实际上会降低性能。特征对齐的实验结果完全符合其物理特性,因为它必须处理全局位移的缩放和所有单个聚类。在预测精化隐式知识实验中,由于串联算子会改变输出的维数,我们只比较了加法算子和乘法算子在实验中的效果。在这组实验中,乘法运算的性能优于加法运算。分析其原因,我们发现中心移位在执行预测时使用加法译码,而锚尺度则使用乘法译码。由于中心坐标为网格边界,影响较小,人工设置锚点的优化空间较大,因此改进更为显著。
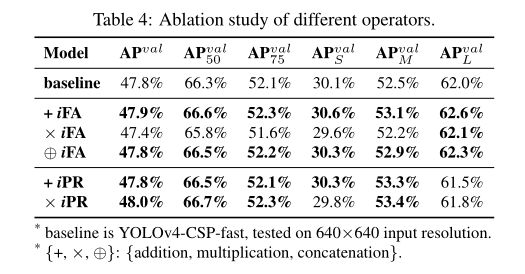

基于上述分析,设计了另外两组实验— { × i F A ∗ , × i P R ∗ } \{× iFA ^*, × iPR ^*\} {×iFA∗,×iPR∗}。在第一组实验 − × i F A ∗ - × iFA ^* −×iFA∗中,将特征空间分割为锚簇级别进行组合和乘法运算,而在第二组实验 − × i P R ∗ - × iPR ^* −×iPR∗中,我们只对预测中的宽度和高度进行乘法运算。以上实验结果如下表所示,经过相应的修改,各项指标的得分都得到了全面的提高。实验表明,在设计如何将显性知识和隐性知识结合时,必须首先考虑组合层的物理意义,以达到乘数效应。
(五)、Modeling implicit knowledge in different ways
我们尝试用不同的方法来建模隐性知识,包括向量、神经网络和矩阵分解。采用神经网络和矩阵分解建模时,隐式先验维的默认值是显式表示维的两倍。这组实验的结果如下表所示。我们可以看到,无论是使用神经网络还是矩阵分解对隐性知识进行建模,都会提高整体效果。其中,采用矩阵分解模型得到了最佳效果,AP、AP50和AP75的性能分别提高了0.2%、0.4%和0.5%。在本实验中,我们演示了使用不同建模方法的效果。同时,我们也证实了隐式表征在未来的潜力。
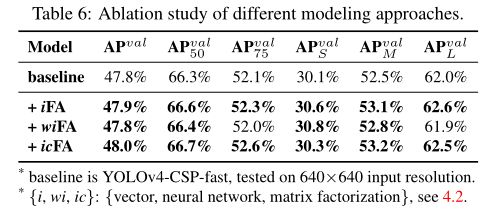
(六)、Analysis of implicit models
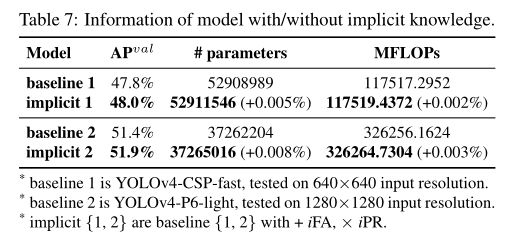
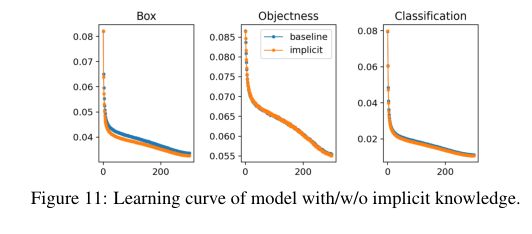
我们分析了具有/w/o隐性知识的模型的参数个数、flop和学习过程,结果分别显示在表7和图11中。从实验数据中我们发现,在具有隐式知识集的实验模型中,我们只增加了不到万分之一的参数量和计算量,就能显著提高模型的性能,训练过程也能快速正确地收敛。
(七)、Implicit knowledge for object detection
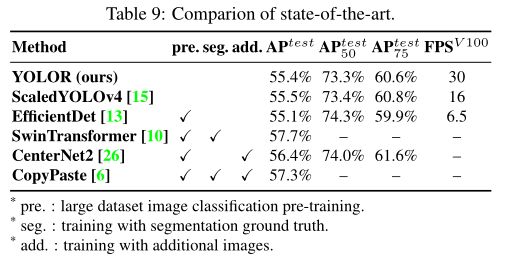
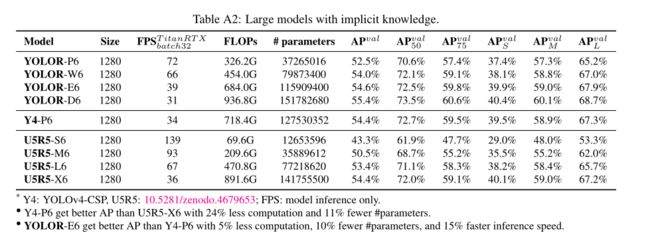
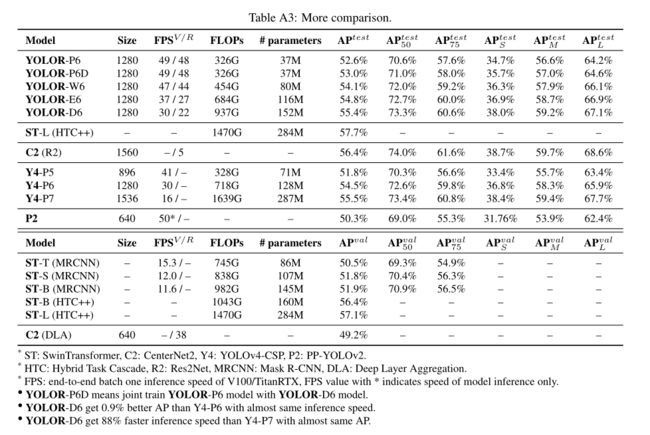
最后,将所提出的方法与目前最先进的目标检测方法的有效性进行了比较。引入隐性知识的好处如下表所示。对于整个训练过程,我们遵循伸缩的yolo4训练过程,即首先从零开始训练300个epoch,然后再微调150个epoch。表9说明了与最新方法的比较。值得注意的是,我们提出的方法没有额外的训练数据和注释。通过引入隐性知识的统一网络,我们仍然获得了与最先进的方法相匹配的结果。


四、附录

我们使用了四种下采样模块,包括(a)离散小波变换(DWT): (b)重组(ReOrg): ,©卷积,(d) CSPNet中使用的CSP卷积
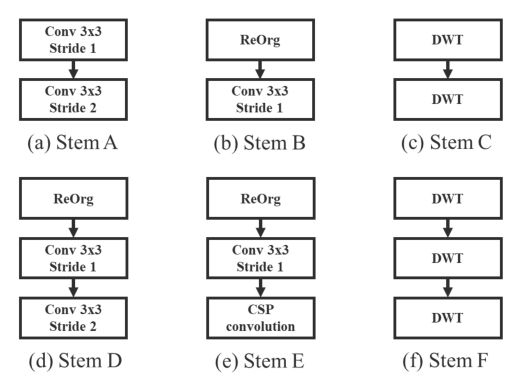
我们使用图A1中的下采样模块形成茎块:(a)用于YOLOv4-CSP, (b)用于YOLOv4-CSP-fast, ©用于YOLOv4-CSPSSS, (d)由称为聚焦层,用于yolov - p6 -light, YOLOR-P6和YOLOR-W6, (e) 用于YOLOR-E6和YOLORD6, (f)用于yolov - csp - ssss。
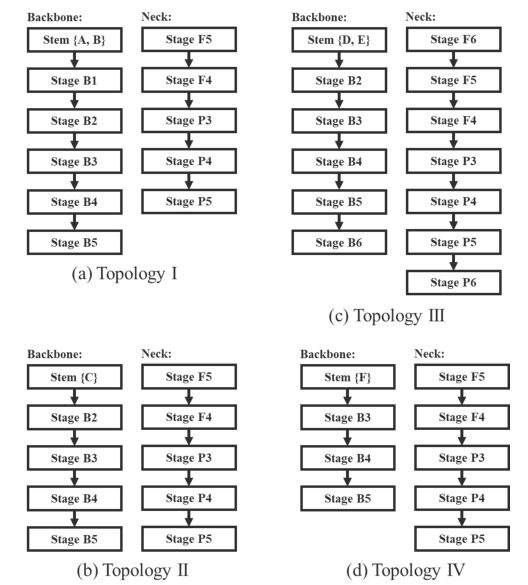
图A3:本文模型可以映射到拓扑的三四种。由于Stem C, D, E包含两个downsampling模块,使用这些Stem block的模型在主干中没有Stage B1,同理Stem F也没有Stage B1和B2。
1、YOLOv4-CSP属于拓扑1,其体系结构在scale - yolov4论文中进行了描述。
2、YOLOv4-CSP-fast是由YOLOv4-CSP改造而成,用Stem B代替YOLOv4-CSP中的Stem A,形成YOLOv4-CSP-fast。
3、YOLOv4-CSP-SSS属于拓扑2,该模型使用Stem C。B2阶段后的拓扑与YOLOv4CSP相同,宽度缩放因子和深度缩放因子分别设为0.5和0.33。然后我们用SiLU激活代替模型中的所有Mish激活。
4、YOLOv4-CSP-SSS是由YOLOv4-CSP-SSS改进而来,模型中YOLOv4-CSP-SSS中的Stem C替换为Stem F。YOLOv4-CSP-SSSS由于茎块包含三个下采样模块,属于拓扑IV。
5、YOLOv4-P6-light属于拓扑3,使用Stem D,基础通道设置为{128,256,384,512,640}。为了优化梯度传播,首先在B*阶段应用CSP融合,并设置B2到B6的重复数为{3,7,7,3,3}。
6、YOLOR-P6与YOLOv4-P6-light具有相同的架构,我们将YOLOv4-P6-light中的所有Mish激活替换为SiLU激活。
7、YOLOR-W6是更宽的YOLOR-P6,基通道设置为{128,256,512,768,1024}
8、YOLOR-E6扩展了YOLOR-W6的宽度,设置宽度缩放因子为1.25,并将所有的卷积下采样模块替换为CSP卷积。
9、YOLOR-D6是较深的YOLOR-E6, B2到B6的重复次数设为{3,15,15,7,7}