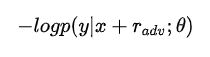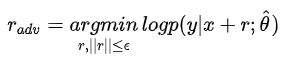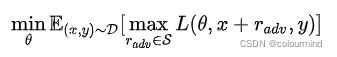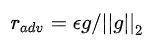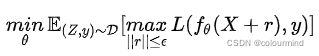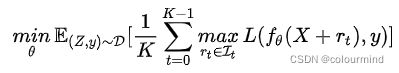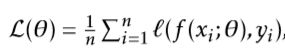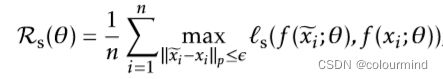NLP中的对抗训练
目录
一、对抗训练的基本概念
二、NLP中常用对抗训练算法的pytorch版本实现
1、FGM——Fast Gradient Method
2、PGD——Projected Gradient Descent
3、FreeLB——Free Large-Batch
4、SMART
对抗训练无论是在CV领域还是在NLP领域都具有举足轻重的地位,本人2021年在NLP比赛中成功的应用了对抗训练,发现对抗训练确确实实能够提升NLP模型在具体任务上的泛化性能,在这篇博客中,我们来聊一聊对抗训练。
一、对抗训练的基本概念
什么是对抗训练呢?
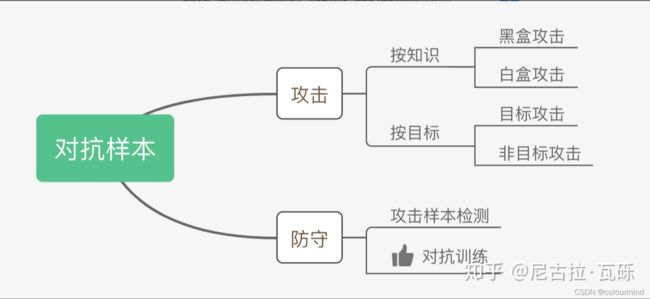
经常在网上看见对抗样本、对抗训练、对抗攻击等名词,有时候真的是对这些名词很模糊头大。借用知乎上的一张图,可以很清晰的得出这些概念和名词的关系。
对抗样本分为对抗攻击和对抗防守,而我们今天要说的对抗训练就是防守中的一种方式,它的核心思想和原理——通过添加扰动来构造一些对抗样本,喂给模型去训练,提高模型在对抗样本上的鲁棒性,同时也在整体上提升模型的泛化性能。
对抗训练的假设
给输入加上扰动之后,输出分布和原Y的分布一致
有监督的数据下使用交叉熵作为损失:
扰动如何得来呢?这需要对抗的思想,即往增大损失的方向增加扰动
公式中的theta表示常数,计算对抗扰动时虽然计算了梯度,但不对参数进行更新,因为当前得到的对抗扰动是对旧参数最优的。整体的思路就是——就是在输入上进行梯度上升(增大loss),在参数上进行梯度下降(减小loss)
Min—MAX公式
聊到对抗训练,就不得不提一下大名鼎鼎的Min—MAX公式了
公式分为2个部分,在MAX部分,就要求内部损失最大化,能找到worst-case的扰动,让模型能够犯错;在MIN部分,则要求经验风险最小化,为了寻找到模型最鲁棒的参数。
CV和NLP的对抗训练
看了很多资料,CV领域和NLP领域时候对抗训练后,模型的泛化能力缺表现的不同,在CV领域添加对抗样本后一般都会损失模型的泛化性能;而在NLP领域则是相反的,采用对抗训练以后一般都会提升模型的性能。为什么是这样呢?我个人认为是NLP扰动是添加到embedding层面上的,而不是直接添加到原始样本上的,这样的微小扰动对语义的改变不大,相当于增加了训练集的正确的样本,从而提升了模型的性能。
NLP中的一句话首先是通过映射到词典,得到初始向量,如果再初始向量上添加扰动,则完全没有意义,把扰动后的初始向量decode后,是得不到有意义的话或者说对抗样本。在NLP领域如何来添加扰动构造对抗样本呢?学者Goodfellow在17年提出在连续的embedding上做扰动,在实现的时候一般是给embedding层参数梯度一个扰动,从而等价的得到embedding的扰动。
二、NLP中常用对抗训练算法的pytorch版本实现
本人没有怎么使用tf,做NLP以来一直用的是torch框架。因此在文中对常用的对抗训练算法进行总结,并附上torch的实现。
1、FGM——Fast Gradient Method
FSGM是每个方向上都走相同的一步,2017年Goodfellow后续提出的FGM则是根据具体的梯度进行scale,得到更好的对抗样本:
算法流程如下:
对于每个x:
1.计算x的前向loss、反向传播得到梯度
2.根据embedding矩阵的梯度计算出r,并加到当前embedding上,相当于x+r
3.计算x+r的前向loss,反向传播得到对抗的梯度,累加到(1)的梯度上
4.将embedding恢复为(1)时的值
5.根据(3)的梯度对参数进行更新具体的实现和插件式使用如下
import torch
class FGM():
'''
Example
# 初始化
fgm = FGM(model,epsilon=1,emb_name='word_embeddings.')
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
'''
def __init__(self, model,emb_name,epsilon=0.5):
# emb_name这个参数要换成你模型中embedding的参数名
self.model = model
self.epsilon = epsilon
self.emb_name = emb_name
self.backup = {}
def attack(self):
for name, param in self.model.named_parameters():
if param.requires_grad and self.emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm!=0 and not torch.isnan(norm):
#对梯度进行scale,然后乘以一个epsilon系数,得到对抗样本
r_at = self.epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self):
for name, param in self.model.named_parameters():
if param.requires_grad and self.emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}2、PGD——Projected Gradient Descent
FGM直接通过epsilon参数一下子算出了对抗扰动,这样得到的可能不是最优的。而后Madry在2018年提出了用Projected Gradient Descent(PGD)的方法,简单的说,就是“小步走,多走几步”,如果走出了扰动半径为 ![]() 的空间,就映射回“球面”上,以保证扰动不要过大:
的空间,就映射回“球面”上,以保证扰动不要过大:
算法流程如下
对于每个x:
1.计算x的前向loss、反向传播得到梯度并备份
对于每步t:
2.根据embedding矩阵的梯度计算出r,并加到当前embedding上,相当于x+r(超出范围则投影回epsilon内)
3.t不是最后一步: 将梯度归0,根据1的x+r计算前后向并得到梯度
4.t是最后一步: 恢复(1)的梯度,计算最后的x+r并将梯度累加到(1)上
5.将embedding恢复为(1)时的值
6.根据(4)的梯度对参数进行更新具体的实现和插件式使用如下
class PGD():
'''
Example
pgd = PGD(model,emb_name='word_embeddings.',epsilon=1.0,alpha=0.3)
K = 3
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
pgd.backup_grad()
# 对抗训练
for t in range(K):
pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
if t != K-1:
model.zero_grad()
else:
pgd.restore_grad()
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
pgd.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
'''
def __init__(self, model, emb_name, epsilon=1., alpha=0.3):
# emb_name这个参数要换成你模型中embedding的参数名
self.model = model
self.emb_name = emb_name
self.epsilon = epsilon
self.alpha = alpha
self.emb_backup = {}
self.grad_backup = {}
def attack(self, is_first_attack=False):
for name, param in self.model.named_parameters():
if param.requires_grad and self.emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0:
r_at = self.alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, self.epsilon)
def restore(self):
for name, param in self.model.named_parameters():
if param.requires_grad and self.emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
r = param_data - self.emb_backup[param_name]
if torch.norm(r) > epsilon:
r = epsilon * r / torch.norm(r)
return self.emb_backup[param_name] + r
def backup_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad and param.grad is not None:
self.grad_backup[name] = param.grad.clone()
def restore_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad and param.grad is not None:
param.grad = self.grad_backup[name]相比较与FGM,PGD采用了多走几步的方式,显而易见计算量加倍了,因此计算时间也是加倍的,效率存在一定的问题,需要我们自己来决策。
3、FreeLB——Free Large-Batch
该算法是2020年提出来的,这个算法之前还有2019年的FreeAT(Free Adversarial Training)以及YOPO(You Only Propagate Once)两种算法,它们都是在保证效果的同时减小PGD的计算量,提升效率。FreeLB认为,FreeAT和YOPO对于获得最优r (inner max)的计算都存在问题,因此提出了一种类似PGD的方法。只不过PGD只使用了最后一步x+r输出的梯度,而FreeLB取了每次迭代r输出梯度的平均值,相当于把输入看作一个K倍大的虚拟batch,由[X+r1, X+r2, ..., X+rk]拼接而成的。PGD和FreeLB公式如下:
PGD取一步的梯度,而FreeLB取的是K步的平均值。
算法流程
对于每个输入x:
1、通过均匀分布初始化扰动r,初始化梯度g为0,设置步数为K
对于每步t=1...K:
2、根据x+r计算前向loss和后向梯度g1,累计梯度g=g+g1/k
3、更新扰动r,更新方式跟PGD一样
4、根据g更新梯度实现代码如下
class FreeLB(object):
"""
Example
model =
loss_fun =
freelb = FreeLB(loss_fun,adv_K=3,adv_lr=1e-2,adv_init_mag=2e-2)
for batch_input, batch_label in data:
inputs = {'input_ids':...,...,'labels':batch_label}
#freelb.attack中进行了多次loss.backward()
loss = freelb.attack(model,inputs)
loss.backward()
optimizer.step()
model.zero_grad()
"""
def __init__(self, loss_fun, adv_K=3, adv_lr=1e-2, adv_init_mag=2e-2, adv_max_norm=0., adv_norm_type='l2', base_model='bert'):
"""
初始化
:param loss_fun: 任务适配的损失函数
:param adv_K: 每次扰动对抗的小步数,最少是1 一般是3
:param adv_lr: 扰动的学习率1e-2
:param adv_init_mag: 初始扰动的参数 2e-2
:param adv_max_norm:0 set to 0 to be unlimited 扰动的大小限制 torch.clamp()等来实现
:param adv_norm_type: ["l2", "linf"]
:param base_model: 默认的bert
"""
self.adv_K = adv_K
self.adv_lr = adv_lr
self.adv_max_norm = adv_max_norm
self.adv_init_mag = adv_init_mag # adv-training initialize with what magnitude, 即我们用多大的数值初始化delta
self.adv_norm_type = adv_norm_type
self.base_model = base_model
self.loss_fun = loss_fun
def attack(self, model, inputs, labels, gradient_accumulation_steps=1):
#model 可以放在初始化中
input_ids = inputs['input_ids']
#得到初始化的embedding
#从bert模型中拿出embeddings层中的word_embeddings来进行input_ids到embedding的变换
if isinstance(model, torch.nn.DataParallel):
embeds_init = getattr(model.module, self.base_model).embeddings.word_embeddings(input_ids)
else:
embeds_init = getattr(model, self.base_model).embeddings.word_embeddings(input_ids)
# embeds_init = model.encoder.embeddings.word_embeddings(input_ids)
if self.adv_init_mag > 0: # 影响attack首步是基于原始梯度(delta=0),还是对抗梯度(delta!=0)
#类型和设备转换
input_mask = inputs['attention_mask'].to(embeds_init)
input_lengths = torch.sum(input_mask, 1)
if self.adv_norm_type == "l2":
delta = torch.zeros_like(embeds_init).uniform_(-1, 1) * input_mask.unsqueeze(2)
dims = input_lengths * embeds_init.size(-1)
mag = self.adv_init_mag / torch.sqrt(dims)
delta = (delta * mag.view(-1, 1, 1)).detach()
elif self.adv_norm_type == "linf":
delta = torch.zeros_like(embeds_init).uniform_(-self.adv_init_mag, self.adv_init_mag)
delta = delta * input_mask.unsqueeze(2)
else:
delta = torch.zeros_like(embeds_init) # 扰动初始化
for astep in range(self.adv_K):
delta.requires_grad_()
#bert transformer类模型在输入的时候inputs_embeds 和 input_ids 二选一 不然会报错。。。。。。源码
inputs['inputs_embeds'] = delta + embeds_init # 累积一次扰动delta
inputs['input_ids'] = None
# 下游任务的模型,我这里在模型输出没有给出loss 要自己计算原始loss
logits = model(inputs)
loss = self.loss_fun(logits, labels)
loss = loss/self.adv_K
loss = loss.mean() # mean() to average on multi-gpu parallel training
loss = loss / gradient_accumulation_steps
loss.backward()
if astep == self.adv_K - 1:
# further updates on delta
break
delta_grad = delta.grad.clone().detach() # 备份扰动的grad
if self.adv_norm_type == "l2":
denorm = torch.norm(delta_grad.view(delta_grad.size(0), -1), dim=1).view(-1, 1, 1)
denorm = torch.clamp(denorm, min=1e-8)
delta = (delta + self.adv_lr * delta_grad / denorm).detach()
if self.adv_max_norm > 0:
delta_norm = torch.norm(delta.view(delta.size(0), -1).float(), p=2, dim=1).detach()
exceed_mask = (delta_norm > self.adv_max_norm).to(embeds_init)
reweights = (self.adv_max_norm / delta_norm * exceed_mask + (1 - exceed_mask)).view(-1, 1, 1)
delta = (delta * reweights).detach()
elif self.adv_norm_type == "linf":
denorm = torch.norm(delta_grad.view(delta_grad.size(0), -1), dim=1, p=float("inf")).view(-1, 1, 1) # p='inf',无穷范数,获取绝对值最大者
denorm = torch.clamp(denorm, min=1e-8) # 类似np.clip,将数值夹逼到(min, max)之间
delta = (delta + self.adv_lr * delta_grad / denorm).detach() # 计算该步的delta,然后累加到原delta值上(梯度上升)
if self.adv_max_norm > 0:
delta = torch.clamp(delta, -self.adv_max_norm, self.adv_max_norm).detach()
else:
raise ValueError("Norm type {} not specified.".format(self.adv_norm_type))
if isinstance(model, torch.nn.DataParallel):
embeds_init = getattr(model.module, self.base_model).embeddings.word_embeddings(input_ids)
else:
embeds_init = getattr(model, self.base_model).embeddings.word_embeddings(input_ids)
return loss4、SMART
2020年的论文SMART: Robust and Efficient Fine-Tuning for Pre-trained Natural Language Models through Principled Regularized Optimization,针对预训练的自然语言模型提出了一种高效的和鲁棒的正则化优化方法,具体的提出了2个方法
a.平滑性归纳对抗性正则化 SMoothness-inducing Adversarial Regularization,提升模型鲁棒性
b.优化算法 Bregman proximal point optimization,避免灾难性遗忘
平滑性归纳对抗性正则化
这里我们关注对平滑性归纳对抗性正则化方法,平滑性归纳对抗性正则化本质上就是解决微调中的一个优化问题
其中F和![]() 表示模型和模型参数,
表示模型和模型参数,![]() 是损失函数,定义如下:
是损失函数,定义如下:
ℓ(·, ·)是取决于目标任务的损失函数,x是样本,y是标签。λs > 0是一个调整参数,Rs(θ)是平滑度归纳的对抗性正则化项。这里我们将Rs(θ)定义为
其中ε>0是一个优化参数。请注意,对于分类任务,f (·; θ)输出的是一个概率单数,ℓs被选为对称的KL-散度
对于回归任务,f (·; θ)输出一个标量,ℓs被选为平方损失,即ℓs(p, q) = (p-q)2,可以选择MSEloss
算法的整体流程
训练过程中,对每一步训练迭代
1、从数据集中得到一个mini-bach
2、给mini-bach中的样本x添加一个正态扰动v,得到新的样本
3、把这个新的样本喂入模型中更新m轮,每一轮都更新一个扰动,扰动学习率乘以梯度scale
4、m轮后采用动量的方式把之前的旧模型参数+更新参数得到每一轮的最终新参数
重复1-4步骤,完成模型的训练。
以上就是SMART中平滑性归纳对抗性正则化方法的数学原理和思想,下面来阅读一下官方的源码。
SMART的平滑性归纳对抗性正则化实现和应用
源码SmartPerturbation|Smart对抗扰动loss计算模块——核心代码在于forward()中generate_noise的初始化和noise更新以及scale
#初始noise扰动
def generate_noise(embed, mask, epsilon=1e-5):
noise = embed.data.new(embed.size()).normal_(0, 1) * epsilon
noise.detach()
noise.requires_grad_()
return noise
#梯度scale
def _norm_grad(self, grad, eff_grad=None, sentence_level=False):
if self.norm_p == 'l2':
if sentence_level:
direction = grad / (torch.norm(grad, dim=(-2, -1), keepdim=True) + self.epsilon)
else:
direction = grad / (torch.norm(grad, dim=-1, keepdim=True) + self.epsilon)
elif self.norm_p == 'l1':
direction = grad.sign()
else:
if sentence_level:
direction = grad / (grad.abs().max((-2, -1), keepdim=True)[0] + self.epsilon)
else:
direction = grad / (grad.abs().max(-1, keepdim=True)[0] + self.epsilon)
eff_direction = eff_grad / (grad.abs().max(-1, keepdim=True)[0] + self.epsilon)
return direction, eff_direction
#对抗loss输出
def forward(self, model,
logits,
input_ids,
token_type_ids,
attention_mask,
premise_mask=None,
hyp_mask=None,
task_id=0,
task_type=TaskType.Classification,
pairwise=1):
# adv training
assert task_type in set([TaskType.Classification, TaskType.Ranking, TaskType.Regression]), 'Donot support {} yet'.format(task_type)
vat_args = [input_ids, token_type_ids, attention_mask, premise_mask, hyp_mask, task_id, 1]
# init delta
embed = model(*vat_args)#bert模型的输出embedding
#embed生成noise
noise = generate_noise(embed, attention_mask, epsilon=self.noise_var)
#更新K轮
for step in range(0, self.K):
vat_args = [input_ids, token_type_ids, attention_mask, premise_mask, hyp_mask, task_id, 2, embed + noise]
#noise+embed得到对抗样本的输出logits
adv_logits = model(*vat_args)
if task_type == TaskType.Regression:
#回归任务做mseloss
adv_loss = F.mse_loss(adv_logits, logits.detach(), reduction='sum')
else:
if task_type == TaskType.Ranking:
adv_logits = adv_logits.view(-1, pairwise)
#分类任务进行对称散度loss
adv_loss = stable_kl(adv_logits, logits.detach(), reduce=False)
#loss对noise求梯度
delta_grad, = torch.autograd.grad(adv_loss, noise, only_inputs=True, retain_graph=False)
#梯度scale
norm = delta_grad.norm()
if (torch.isnan(norm) or torch.isinf(norm)):
return 0
#梯度的更新值
eff_delta_grad = delta_grad * self.step_size
#noise的更新
delta_grad = noise + delta_grad * self.step_size
#得到新的scale的noise
noise, eff_noise = self._norm_grad(delta_grad, eff_grad=eff_delta_grad, sentence_level=self.norm_level)
noise = noise.detach()
noise.requires_grad_()
vat_args = [input_ids, token_type_ids, attention_mask, premise_mask, hyp_mask, task_id, 2, embed + noise]
#把找到的最终noise扰动添加到embed上得到对抗样本
adv_logits = model(*vat_args)
if task_type == TaskType.Ranking:
adv_logits = adv_logits.view(-1, pairwise)
adv_lc = self.loss_map[task_id]
#输出对抗loss
adv_loss = adv_lc(logits, adv_logits, ignore_index=-1)
return adv_loss, embed.detach().abs().mean(), eff_noise.detach().abs().mean()整理一下自己实现一版
import torch
import torch.nn.functional as F
class SmartPerturbation():
"""
step_size noise扰动学习率
epsilon 梯度scale时防止分母为0
norm_p 梯度scale采用的范式
noise_var 扰动初始化系数
loss_map 字典,loss函数的类型{"0":mse(),....}
使用方法
optimizer =
model =
loss_func =
loss_map = {"0":loss_fun0,"1":loss_fun1,...}
smart_adv = SmartPerturbation(model,epsilon,step_size,noise_var,loss_map)
for batch_input, batch_label in data:
inputs = {'input_ids':...,...,'labels':batch_label}
logits = model(**inputs)
loss = loss_func(logits,batch_label)
loss_adv = smart_adv.forward(logits,input_ids,token_type_ids,attention_mask,)
loss = loss + adv_alpha*loss_adv
loss.backward()
optimizer.step()
model.zero_grad()
"""
def __init__(self,
model,
epsilon=1e-6,
multi_gpu_on=False,
step_size=1e-3,
noise_var=1e-5,
norm_p='inf',
k=1,
fp16=False,
loss_map={},
norm_level=0):
super(SmartPerturbation, self).__init__()
self.epsilon = epsilon
# eta
self.step_size = step_size
self.multi_gpu_on = multi_gpu_on
self.fp16 = fp16
self.K = k
# sigma
self.noise_var = noise_var
self.norm_p = norm_p
self.model = model
self.loss_map = loss_map
self.norm_level = norm_level > 0
assert len(loss_map) > 0
# 梯度scale
def _norm_grad(self, grad, eff_grad=None, sentence_level=False):
if self.norm_p == 'l2':
if sentence_level:
direction = grad / (torch.norm(grad, dim=(-2, -1), keepdim=True) + self.epsilon)
else:
direction = grad / (torch.norm(grad, dim=-1, keepdim=True) + self.epsilon)
elif self.norm_p == 'l1':
direction = grad.sign()
else:
if sentence_level:
direction = grad / (grad.abs().max((-2, -1), keepdim=True)[0] + self.epsilon)
else:
direction = grad / (grad.abs().max(-1, keepdim=True)[0] + self.epsilon)
eff_direction = eff_grad / (grad.abs().max(-1, keepdim=True)[0] + self.epsilon)
return direction, eff_direction
# 初始noise扰动
def generate_noise(self,embed, mask, epsilon=1e-5):
noise = embed.data.new(embed.size()).normal_(0, 1) * epsilon
noise.detach()
noise.requires_grad_()
return noise
#对称散度loss
def stable_kl(self,logit, target, epsilon=1e-6, reduce=True):
logit = logit.view(-1, logit.size(-1)).float()
target = target.view(-1, target.size(-1)).float()
bs = logit.size(0)
p = F.log_softmax(logit, 1).exp()
y = F.log_softmax(target, 1).exp()
rp = -(1.0 / (p + epsilon) - 1 + epsilon).detach().log()
ry = -(1.0 / (y + epsilon) - 1 + epsilon).detach().log()
if reduce:
return (p * (rp - ry) * 2).sum() / bs
else:
return (p * (rp - ry) * 2).sum()
# 对抗loss输出
def forward(self,
logits,
input_ids,
token_type_ids,
attention_mask,
task_id=0,
task_type="Classification",
pairwise=1):
# adv training
assert task_type in set(['Classification', 'Ranking', 'Regression']), 'Donot support {} yet'.format(task_type)
vat_args = {'input_ids': input_ids, 'attention_mask': attention_mask, 'token_type_ids': token_type_ids}
# init delta
embed = self.model(**vat_args) #embed [B,S,h_dim] h_dim=768
# embed生成noise
noise = self.generate_noise(embed, attention_mask, epsilon=self.noise_var)
#noise更新K轮
for step in range(0, self.K):
vat_args = {'inputs_embeds':embed + noise}
# noise+embed得到对抗样本的输出logits
adv_logits = self.model(**vat_args)
if task_type == 'Regression':
adv_loss = F.mse_loss(adv_logits, logits.detach(), reduction='sum')
else:
if task_type == 'Ranking':
adv_logits = adv_logits.view(-1, pairwise)
adv_loss = self.stable_kl(adv_logits, logits.detach(), reduce=False)
#得到noise的梯度
delta_grad, = torch.autograd.grad(adv_loss, noise, only_inputs=True, retain_graph=False)
norm = delta_grad.norm()
if (torch.isnan(norm) or torch.isinf(norm)):
return 0
eff_delta_grad = delta_grad * self.step_size
delta_grad = noise + delta_grad * self.step_size
# 得到新的scale的noise
noise, eff_noise = self._norm_grad(delta_grad, eff_grad=eff_delta_grad, sentence_level=self.norm_level)
noise = noise.detach()
noise.requires_grad_()
vat_args = {'inputs_embeds': embed + noise}
adv_logits = self.model(**vat_args)
if task_type == 'Ranking':
adv_logits = adv_logits.view(-1, pairwise)
adv_lc = self.loss_map[task_id]
#计算对抗样本的对抗损失
adv_loss = adv_lc(logits, adv_logits, ignore_index=-1)
return adv_loss使用起来也很简单,想插件一下,只需要添加几行代码在训练代码中。
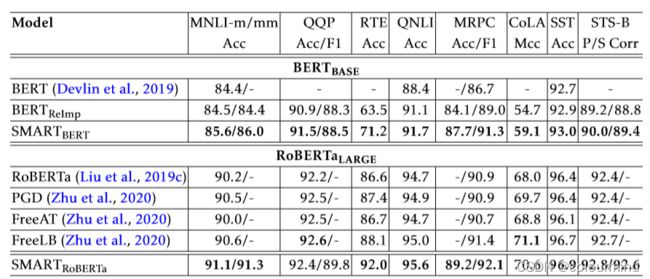
具体的效果怎么样呢?SMART中给出了PGD、FreeAT、FreeLB和SMART的对比结果,模型采用的是RoBERTa_LARGE
SMART几乎在给出几个任务中效果都要比之前的所有对抗训练的方法要优越,那再中文的数据集上效果怎么样呢?这里时间有限,本人就不做详细的对比了,或者以后有空了再来填坑。
文中给出了详细的算法代码,都是插件式使用,想要验证效果到底怎么样,都很简单。本人在2021年参加CCF自然语言处理中得到的经验,在不同的数据集和不同的任务下,FGM、PGD和FreeLB均有所提升,但是谁更好,这个是不一定的,有的比赛使用FGM能得到最佳得分,有的是PGD,SMART当时没有来得及实验。
参考文章
【炼丹技巧】功守道:NLP中的对抗训练 + PyTorch实现
一文搞懂NLP中的对抗训练FGSM/FGM/PGD/FreeAT/YOPO/FreeLB/SMART
SMART: 通过原则的正则化优化对预训练的自然语言模型进行鲁棒和高效的微调
SmartPerturbation源码
MTDNNModel源码