EM算法原理和实现的学习总结

0. 写在前面（学习过程总结）

我的数学基础不好，所以EM算法折腾了不少时间才真正理解。

我对EM算法的理解过程经历了如下几个阶段：

1. 看《统计学习方法》上的第9章 EM算法及其推广，对EM算法需要解决的问题和原理有了一个初步的印象；
   （这个时候其实并不是完全明白）
2. 根据 EM算法整理及其python实现 这篇博客，再梳理一遍原理，然后敲了一遍代码。
   （这个时候已经对EM中 e-step 和 m-step 的原理和步骤有比较好的理解了，纸上得来终觉浅，绝知代码要手写）
3. 然后复习了HMM的原理，HMM的无监督学习方法就是类似EM算法的鲍姆-韦尔奇算法，这里其实主要目的是看HMM需要解决的问题，也就是对EM算法需要解决的问题能够有更深的理解，这样看公式的时候能够带入HMM的问题，公式就不会那么抽象了。
4. 最后看了博客 EM算法原理总结-刘建平，重新梳理一遍原理，他的博客内容和《统计学习方法》内容差不多，可能更加简练一些，因为之前已经有了基础知识，再回过头来看公式就会觉得很容易理解了。

1. EM算法的原理

EM算法是一种迭代算法，它也称为期望最大化（Expectation-Maximum,简称EM）算法。
EM算法分为两步骤：
（1）E步：期望
（2）M步：求极大
然后不断重复1、2两步，直到参数收敛，就得到了需要的模型参数。

EM算法的求解过程其实就是先猜测一组模型参数（具体实现的时候可以都设为0或者随机初始化，看具体要求），然后基于猜测的模型参数和观测序列来极大化对数似然函数，求解模型参数。

2. EM算法的公式推导

EM算法的推导可以看下博客：EM算法原理总结-刘建平，写的非常精炼。

下面的内容基于这一篇博客来写的，加上了我自己对公式的理解和推导过程。

对于$m$个样本观察数据$x=(x(1),x(2),...,x(m))$中，找出样本的模型参数$\theta$, 极大化模型分布的对数似然函数如下：

$$\arg \underset{\theta }{\max }L(\theta )=\arg \underset{\theta }{\max }\sum _{i=1}^{m}logP(x^{(i)};\theta )\text{\hspace{1em}(1)}$$

(备注：这里是对应刘建平老师博客的第一条公式，原博是 $\theta =$，我觉得这里不太好理解，应该是关于 $\theta$ 的对数似然函数，因此做了修改)

如果观察数据$x$序列，有对应的无法观察到的隐含数据$z=(z(1),z(2),...,z(m))$，那么对数似然函数的公式中就要再加上一个变量，此时我们的极大化模型分布的对数似然函数如下：

$$\begin{gathered} \arg \underset{\theta }{\max }L(\theta )=\arg \underset{\theta }{\max }\sum _{i=1}^{m}logP(x^{(i)};\theta ) \\ =\arg \underset{\theta }{\max }\sum _{i=1}^{m}log\sum _{z^{(i)}}P(x^{(i)},z^{(i)};\theta )\text{\hspace{1em}(2)} \end{gathered}$$

这个公式也不难理解，以HMM做实体标注为例，观测序列是输出多个词，隐藏状态序列是每个词对应的label，那么这里的 $z^{(i)}$ 就是隐藏状态label i 的概率。

所以公式里的 $\sum z^{(i)}$ 就是对于每一个观测序列，求它在 所有隐藏状态序列的概率和。

上面这个公式（2）是没有 办法直接求出$\theta$的。因此需要一些特殊的技巧，我们首先对这个式子进行缩放如下：

$$\sum _{i=1}^{m}log\sum _{z^{(i)}}P(x^{(i)},z^{(i)};\theta )=\sum _{i=1}^{m}log\sum _{z^{(i)}}{Q}_i(z^{(i)})\frac{P(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}\text{\hspace{1em}(3)}$$

这一步的变化就是引入了一个关于$z$的分布函数 $Q(z)$。

为了求解上述公式（3），这里需要引入 琴生不等式：

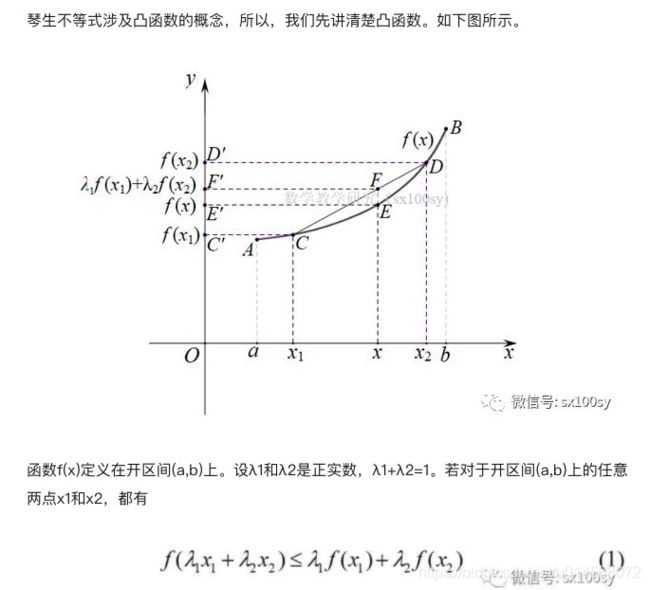
因为 $log$函数是凹函数（下图红色线），所有图片中的不等号用于EM公式推导的时候要反过来。

因此，根据琴生不等式，我们可以把公式（3）写成下面的形式

$$\sum _{i=1}^{m}log\sum _{z^{(i)}}{Q}_i(z^{(i)})\frac{P(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}\ge \sum _{i=1}^m\sum _{z^{(i)}}{Q}_i(z^{(i)})log\frac{P(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}\text{\hspace{1em}(4)}$$
其中,
$$\sum _z{Q}_i(z^{(i)})=1\text{\hspace{1em}(5)}$$

从图1中可以看出，琴生不等式中等号成立的条件是：$f(x)$中的$x$是常数，也就是说凸/凹函数变成一条直线，这样图1中的E和F点就会重合，等号成立。

对应到EM算法的公式（4）中，要想等号成立，我们需要：
$$\frac{P(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}=c，c为常数\text{\hspace{1em}(6)}$$
把分母移到公式右边可以得到
$$P(x^{(i)},z^{(i)};\theta )=c{Q}_i(z^{(i)})，c为常数\text{\hspace{1em}(7)}$$
两边同时对$z$求和可以得到
$$\sum _{z}P(x^{(i)},z^{(i)};\theta )=c\sum _z{Q}_i(z^{(i)})，c为常数\text{\hspace{1em}(8)}$$
把（5）带入（8）中可以得到

$$\sum _{z}P(x^{(i)},z^{(i)};\theta )=c，c为常数\text{\hspace{1em}(9)}$$
把（9）带入（6）中可以得到
$$\frac{P(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}=\sum _{z}P(x^{(i)},z^{(i)};\theta )\text{\hspace{1em}(10)}$$
交换下分母位置，即，
$$\begin{gathered} Q_i(z^{(i)})=\frac{P(x^{(i)},z^{(i)};\theta )}{{\sum }_{z}P(x^{(i)},z^{(i)};\theta )} \\ =\frac{P(x^{(i)},z^{(i)};\theta )}{P(x^{(i)};\theta )} \\ =P(z^{(i)}|x^{(i)};\theta )\text{\hspace{1em}(11)} \end{gathered}$$
（条件概率公式 $P(B|A)=\frac{P(AB)}{P(A)}$）

即，当公式（11） $Q_i(z^{(i)})=P(z^{(i)}|x^{(i)};\theta )$ 成立的时候，公式（4）中的不等号才会成立。
也就是说，等号成立时，公式（4）右边的部分就是目标函数的下界。
则我们对目标函数求最大值的问题，可以等价地转换为对其下界求最大值，即
$$\arg \underset{\theta }{\max }\sum _{i=1}^m\sum _{z^{(i)}}{Q}_i(z^{(i)})log\frac{P(x^{(i)},z^{(i)};\theta )}{Q_i(z^{(i)})}\text{\hspace{1em}(12)}$$

把log里的分式展开可以得到下面
$$\arg \underset{\theta }{\max }\sum _{i=1}^m\sum _{z^{(i)}}{Q}_i(z^{(i)})logP(x^{(i)},z^{(i)};\theta )-Q_i(z^{(i)})log{Q}_i(z^{(i)})\text{\hspace{1em}(13)}$$
刘建平老师的博客里说“去掉上式中为常数的部分”，这里所说的常数部分就是$Q_i(z^{(i)})log{Q}_i(z^{(i)})$ 这个部分是常量，评论里也做了解释：

我试着理解了一下，这部分要带入EM算法的两个步骤了，$Q_i(z^{(i)})$ 是在E步计算的，在给定了猜测的隐藏状态的分布和模型参数之后，$Q_i(z^{(i)})$ 就是一个确定值了，在完成本轮的EM之前都是常数，所以在当前的M步中最大化目标函数的时候可以把 $Q_i(z^{(i)})log{Q}_i(z^{(i)})$ 作为常数去掉。

在计算完成之后再对隐藏状态的分布和模型参数进行迭代修正。

综上，我们需要极大化的对数似然下界为：

$$\arg \underset{\theta }{\max }\sum _{i=1}^m\sum _{z^{(i)}}{Q}_i(z^{(i)})logP(x^{(i)},z^{(i)};\theta )\text{\hspace{1em}(14)}$$
这里对应的就是EM算法的M步。
对于公式（14）进行求导为0的最值求解之后，获得的$\theta$值就可以作为下一轮迭代的初始值（也就是取代掉一开始的猜测值）

至此就完成了EM算法的全部推导。

3. EM算法的代码实现（双硬币问题为例子）

EM算法的代码实现代码主要是参见了博客：EM算法整理及其python实现（不过这个博客看起来也是转载的）

以双硬币问题为例。

假设有两枚硬币A、B，以相同的概率随机选择一个硬币，进行如下的抛硬币实验：共做5次实验，每次实验独立的抛十次，结果如图中a所示，例如某次实验产生了H、T、T、T、H、H、T、H、T、H，H代表正面朝上。

假设我们并不知道这5次实验抛的是硬币A还是B，那么5次的硬币选择就是一个同样需要估计的隐藏状态，如图b。

（图b可以仔细看看，能够帮助理解代码和原理）

下面的代码是EM算法解决双硬币问题（同上图b），我自己手敲了一遍，加上了自己的理解。
（不知道是否理解正确，如有问题欢迎讨论和指正）

class EMAlgorithm():
    '''
    代码参考博客：https://blog.csdn.net/brave_stone/article/details/80423784
    '''

    def em_single_step(self, priors, observations):
        '''
        EM 算法单次迭代
        :param priors，目标的先验概率（随即初始化，不断迭代）
        :param observations: 观测矩阵，shape (m,n)，这里就是5次实验硬币观测的结果
        :return:
            cur_priors: 当前轮次计算得到的目标概率
        '''
        # theta_a 表示硬币 A 出现正面的概率
        # theta_b 表示硬币 B 出现正面的概率
        theta_a, theta_b = priors[0], priors[1]
        # count 用来记录基于当前轮的先验theta_a和theta_b，当前 A和B 出现正/反面的次数
        count = {
            "A": [0, 0],
            "B": [0, 0]
        }
		# 公式里的Q(z)对应这里的就是每次实验选择a还是b这个隐藏状态的分布
        
		# E步
        # 遍历每次抛硬币的观测序列，在这里就是遍历5次实验
        # 对应到公式中就是在m个样本上求和
        for observation in observations:
            observ_num = len(observation)  # 每次抛硬币次数，样例中是10次
            num_head = observation.sum()  # 正面=1，计算正面出现的次数
            num_tail = observ_num - num_head  # 反面=0，计算反面出现的次数

            # print(num_head, num_tail)
            # 计算在当前的先验概率下，得到A、B硬币观测结果出现的概率
			# pa 表示在当前theta_a的情况下，A硬币出现当前观测序列的概率
            pa = theta_a**num_head + (1-theta_a)**num_tail
            # pb 同理，B硬币出现当前观测序列的概率
            pb = theta_b**num_head + (1-theta_b)**num_tail
            # 则可以计算隐藏状态的分布，也就是公式里的Q(z)
            P_A = pa / (pa+pb)  # P_A 计算的是当前轮抛 硬币A 的概率
            P_B = pb / (pa+pb)  # P_B 同理，是当前轮抛的是 B硬币的概率
            
            # 给定theta和观测序列x，Q(z)就可以认为是常数，所以在公式里求最大值的时候可以直接去掉
            # 根据Q(z)和观测结果，从期望的角度，计算 A、B硬币 当前轮次应该出现的正反次数
            #  也就是 count(x,Q(z);theta)，先算count是为了后面算概率p
            count["A"][0] += num_head * P_A
            count["A"][1] += num_tail * P_A
            count["B"][0] += num_head * P_B
            count["B"][1] += num_tail * P_B

        # M步，这里为啥可以直接用频率计算结果作为更新的 theta_a 和 theta_b 呢，我理解是这样的：
        # 根据公式，此时的对数似然函数是关于未知模型参数 theta_a 和 theta_b 的
        # 对目标函数求导=0后求解得到的最大值就是x的期望
        theta_a = count["A"][0] / (count["A"][1] + count["A"][0])
        theta_b = count["B"][0] / (count["B"][1] + count["B"][0])
        return [theta_a, theta_b]

    def em(self, observations, priors, iteration=1000, stop_early=1e-10):
    	'''
    	完整的em算法，多次迭代，直到收敛
    	:param iteration，迭代次数
    	:param stop_early，收敛的阈值
    	'''
        itr = 0
        new_priors = []
        while itr < iteration:
        	# 单次em计算 
            new_priors = self.em_single_step(priors, observations)
            if math.fabs(priors[0] - new_priors[0]) < stop_early:
                break
            priors = new_priors
            itr += 1
            print('iter = {}, prior = {}'.format(itr, priors))
        return [new_priors, itr]

测试代码：

if __name__ == '__main__':
    # 硬币投掷结果观测序列
    observations = np.array([[1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
                             [1, 1, 1, 1, 1, 1, 1, 1, 0, 1],
                             [1, 1, 1, 1, 1, 1, 1, 1, 0, 1],
                             [1, 1, 0, 1, 1, 1, 1, 1, 0, 1],
                             [1, 1, 1, 1, 1, 1, 1, 1, 0, 1],
                             [1, 1, 1, 0, 0, 1, 0, 0, 0, 0],
                             [1, 1, 1, 0, 0, 1, 0, 0, 0, 0],
                             [1, 1, 1, 0, 0, 0, 0, 0, 0, 0],
                             [1, 1, 1, 0, 0, 1, 0, 0, 0, 0],
                             [1, 1, 1, 0, 0, 1, 0, 0, 0, 0]])

    em = EMAlgorithm()
    result = em.em(observations, [0.1, 0.9])
    print(result)

输出

iter = 0, prior = [0.1, 0.9], new_priors = [0.6673983693273525, 0.5637164080021754]
iter = 1, prior = [0.6673983693273525, 0.5637164080021754], new_priors = [0.5757908352923907, 0.6722702671924325]
..........
iter = 444, prior = [0.6199999999468074, 0.6200000000531927], new_priors = [0.6200000000507999, 0.6199999999492001]
iter = 445, prior = [0.6200000000507999, 0.6199999999492001], new_priors = [0.6199999999514851, 0.6200000000485149]

[[0.6199999999514851, 0.6200000000485149], 445]

但是很奇怪，这套代码输出的结果 ${\theta }_A$和${\theta }_B$总是最终会趋于相等，不知道是bug还是什么原因。
还有待进一步研究和验证。

参考内容：

• [1] 《统计学系方法 - EM算法及其推广》
• [2] EM算法原理总结-刘建平
• [3] EM算法整理及其python实现