朴素贝叶斯检测垃圾邮件

相关基础理论

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。

联合概率分布

联合概率表示为包含多个条件并且所有的条件都同时成立的概率，记作P(X=a,Y=b)或P(a,b)或P(ab)。比如a是刮风b是下雨，那么既刮风又下雨的概率就是P(a,b)。

联合概率分布就是联合概率在样本空间中的分布情况。

条件概率

条件概率就是A在B条件下发生的概率（记作P(A|B)），我们可以借助韦恩图理解。

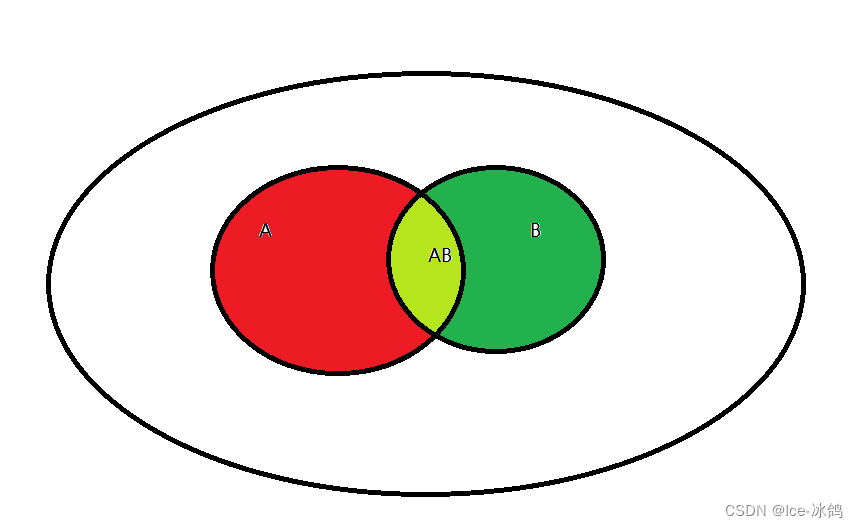
如果要求P(A|B)，那么我们就需要用（青色）A和B的联合概率除以（绿色加青色）B的概率。也就是以下公式：
$$P(A|B)=\frac{P(AB)}{P(B)}$$

贝叶斯定理

在条件概率的基础上同时给出P(A|B)和P(B|A)的公式可以得出以下结论:
$$P(A)=\frac{P(A|B)\times P(B)}{P(B|A)}$$

条件假设

条件独立性假设就是各个特征之间互不影响，每个特征都是条件独立的。这一假设使得朴素贝叶斯法变得简单，但是有时候会牺牲一定的分类准确率。由于条件独立那么$$P(AB)=P(A)\ast P(B)$$

问题分析

本次实验需要进行垃圾邮件检测，实现原理为统计所有邮件中出现的单词频率，并以此作为其出现概率，假设每个单词的使用都是独立的。设A为检测结果（是或否），$B_i$为检测邮件中的某个单词。因此我们仅需计算
$$P(A)=\frac{P(A|B)\times P(B)}{P(B|A)}=\frac{P(A|B)\times {\prod }_{i=0}^{N}P(B_i)}{P(B|A)}$$
即可得到邮件是否为垃圾邮件的概率，通过比较得出最后结果。

数据准备

将邮件用txt形式存储，并分为两类存放于不同的文件夹中。

代码实现

编写朴素贝叶斯类

导入必要库

from numpy import *

过滤社区侮辱性文字

def loadDataSet():
    postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                 ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                 ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                 ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                 ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                 ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0,1,0,1,0,1]    #1 侮辱性文字, 0 正常文字
    return postingList,classVec

建立文档词条

合并所有单词并构造单词集合

#建立文档词条
def createVocabList(dataSet):
    vocabSet=set([])
    for document in dataSet:
        vocabSet=vocabSet|set(document)  #集合合并
    return list(vocabSet)

词集模型

为输入邮件构建单词集合

#词集模型
def setOfWord2Vec(vocabList,inputSet):
    returnVec=zeros(len(vocabList))
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)]=1
        else:
            print("这个单词不在所有的单词向量里面") 
    return  returnVec

词袋模型

#词袋模型
def bagOfword2VecMN(vocabList,inputSet):
    returnVec=[0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)]+=1
    return  returnVec

朴素贝叶斯训练函数

#朴素贝叶斯训练函数
def trainB0(trainMatrix,trainCategory):
    numTrainDocs=len(trainMatrix)
    numwords=len(trainMatrix[0])
    #对于category为0,1 才可以使用sum
    pAbusive=sum(trainCategory)/float(numTrainDocs)
    p0Num=ones(numwords)
    p1Num=ones(numwords)

    p0Denom=2.0
    p1Denom=2.0
    for i in range(numTrainDocs):
        if trainCategory[i]==1:
            p1Num+=trainMatrix[i]
            p1Denom+=sum(trainMatrix[i])
        else:
            p0Num+=trainMatrix[i]
            p0Denom+=sum(trainMatrix[i])

    p1Vect=log(p1Num/p1Denom)
    p0Vect=log(p0Num/p0Denom)
    return p0Vect,p1Vect,pAbusive

朴素贝叶斯分类函数

#朴素贝叶斯分类函数
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
    p1=sum(vec2Classify*p1Vec)+log(pClass1)
    p0=sum(vec2Classify*p0Vec)+log(1-pClass1)
    if p1>p0:
        return 1
    else:
        return 0

朴素贝叶斯预测函数

def testingNB():

    dataSet,classVec=loadDataSet()
    vocabList=createVocabList(dataSet)

    trainMat=[]
    for doc in dataSet:
        trainMat.append(setOfWord2Vec(vocabList,doc))

    p0V,p1V,pAb=trainB0(array(trainMat),array(classVec))
    testEntry=['love','my','dalmation']
    thisDoc=array(setOfWord2Vec(vocabList,testEntry))
    #计算贝叶斯分类结果
    result=classifyNB(thisDoc,p0Vec=p0V,p1Vec=p1V,pClass1=pAb)
    result="正常言论" if result==0 else "侮辱言论"
    print(r"分类结果:",result)

编写预测类

导入必要库

from numpy import *
import re
from os import listdir
from bayes import *
import random

提取单词

#将输入的文本字符串分割成单词list
def textParse(bigString):
    listOfTokens=re.split(r'\W*',bigString)
    return [tok.lower() for tok in listOfTokens if len(tok)>2]

垃圾邮件测试

对所有数据训练出模型后在原数据进行测试得到对应结果

def spamTest():
    docList=[]
    classList=[]
    fullText=[]

    filenameList1=listdir("email/spam")
    for name in filenameList1:
        wordList=textParse(open("email/spam/"+name).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)

    filenameList2=listdir("email/ham")
    for name in filenameList2:
        wordList = textParse(open("email/ham/"+name).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)

    vocabList=createVocabList(docList)
    trainingSet=list(range(len(docList)))

    testSet=[]
    for i in range(int(0.2*len(docList))):
        randIndex=int(random.uniform(0,len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex])
    trainMat=[]
    trainClasses=[]
    for docIndex in trainingSet:
        trainMat.append(setOfWord2Vec(vocabList,docList[docIndex]))
        trainClasses.append(classList[docIndex])

    p0V,p1V,pSpam=trainB0(array(trainMat),array(trainClasses))
    errorCount=0

    for  docIndex in testSet:
        wordVector=setOfWord2Vec(vocabList,docList[docIndex])
        if classifyNB(array(wordVector),p0V,p1V,pSpam)!=classList[docIndex]:
            errorCount+=1
    print (r"错误率:",float(errorCount/float(len(testSet))))

可以看出结果不是很高，毕竟单词之间并不是完全独立。

总结

朴素贝叶斯算法的重点在于各属性的独立性，当属性不独立时使用该方法会导致概率较低甚至极低。原因在于只有独立的情况下才能满足公式$P(AB)=P(A)\ast P(B)$。同时也是该公式大大降低了联合概率的计算难度。