mmpose关键点(四):优化关键点模型(原理与代码讲解,持续更新)
在工程中,模型的运行速度与精度是同样重要的,本文中,我会运用不同的方法去优化比较模型的性能,希望能给大家带来一些实用的trick与经验。
有关键点检测相关经验的同学应该知道,关键点主流方法分为Heatmap-based与Regression-based。
其主要区别在于监督信息的不同,Heatmap-based方法监督模型学习的是高斯概率分布图,即把GroundTruth中每个点渲染成一张高斯热图,最后网络输出为K张特征图对应K个关键点,然后通过argmax来获取最大值点作为估计结果。这种方法由于需要渲染高斯热图,且由于热图中的最值点直接对应了结果,不可避免地需要维持一个相对高分辨率的热图(常见的是64x64,再小的话误差下界过大会造成严重的精度损失),因此也就自然而然导致了很大的计算量和内存开销。
Regression-based方法则非常简单粗暴,直接监督模型学习坐标值,计算坐标值的L1或L2 loss。由于不需要渲染高斯热图,也不需要维持高分辨率,网络输出的特征图可以很小(比如14x14甚至7x7),拿Resnet-50来举例的话,FLOPs是Heatmap-based方法的两万分之一,这对于计算力较弱的设备(比如手机)是相当友好的,在实际的项目中,也更多地是采用这种方法。
但是Regression在精度方面始终被Heatmap碾压,Heatmap全卷积的结构能够完整地保留位置信息,因此高斯热图的空间泛化能力更强。而回归方法因为最后需要将图片向量展开成一维向量,reshape过程中会对位置信息有所丢失。除此之外,Regression中的全连接网络需要将位置信息转化为坐标值,对于这种隐晦的信息转化过程,其非线性是极强的,因此不好训练和收敛。
为了更好的提高Regression的精度,我将对其做出一系列优化,并记录于此。
1.regression
我将以mobilenetv3作为所有实验的backbone,搭建MobileNetv3+Deeppose的Baseline。训练数据来自项目,config如下所示。
model = dict(
type='TopDown',
pretrained=None,
backbone=dict(type='MobileNetV3'),
neck=dict(type='GlobalAveragePooling'),
keypoint_head=dict(
type='DeepposeRegressionHead',
in_channels=96,
num_joints=channel_cfg['num_output_channels'],
loss_keypoint=dict(type='SmoothL1Loss', use_target_weight=True)),
train_cfg=dict(),
test_cfg=dict(flip_test=True))
cpu端,模型速度是基于ncnn测试出来的,结论如下:
| 方法 | input size | AP50:95 | acc_pse | time |
|---|---|---|---|---|
| Deeppose | 192*256 | 41.3% | 65% | 2.5ms |
2.Heatmap
同样以mobilenetv3作为backbone,与Regression不同的是,为了获得尺寸为(48,64)的热图特征,我们需要在head添加3个deconv层,将backbone尺寸为(6,8)的特征图上采样至(48,64)。
model = dict(
type='TopDown',
backbone=dict(type='MobileNetV3'),
keypoint_head=dict(
type='TopdownHeatmapSimpleHead',
in_channels=96,
out_channels=channel_cfg['num_output_channels'],
loss_keypoint=dict(type='JointsMSELoss', use_target_weight=True)),
train_cfg=dict(),
test_cfg=dict(
flip_test=True,
post_process='default',
shift_heatmap=True,
modulate_kernel=11))
cpu端,模型速度是基于ncnn测试出来的,结论如下:
| 方法 | input size | AP50:95 | acc_pse | time |
|---|---|---|---|---|
| Deeppose | 192*256 | 41.3% | 65% | 2.5ms |
| Heatmap | 192*256 | 67.5% | 93% | 60ms |
由于head层结构不同,参数量变大,导致推理时间剧增。Heatmap全卷积的结构能够完整地保留位置信息,因此高斯热图的空间泛化能力更强。而回归方法因为最后需要将图片向量展开成一维向量,reshape过程中会对位置信息有所丢失。除此之外,Regression中的全连接网络需要将位置信息转化为坐标值,对于这种隐晦的信息转化过程,其非线性是极强的,因此不好训练和收敛。
3.RLE
Regression只关心离散概率分布的均值(只预测坐标值,一个均值可以对应无数种分布),丢失了 μ \mu μ周围分布的信息,相较于heatmap显示地将GT分布(人为设置方差 σ \sigma σ)标注成高斯热图并作为学习目标,RLE隐性的极大似然损失可以帮助regression确定概率分布均值与方差,构造真实误差概率分布,从而更好的回归坐标。
model = dict(
type='TopDown',
backbone=dict(type='MobileNetV3'),
neck=dict(type='GlobalAveragePooling'),
keypoint_head=dict(
type='DeepposeRegressionHead',
in_channels=96,
num_joints=channel_cfg['num_output_channels'],
loss_keypoint=dict(
type='RLELoss',
use_target_weight=True,
size_average=True,
residual=True),
out_sigma=True),
train_cfg=dict(),
test_cfg=dict(flip_test=True, regression_flip_shift=True))
mmpose已经实现了RLE loss,我们只需要在config上添加loss_keypoint=RLELoss就能够运行。
| 方法 | input size | AP50:95 | acc_pse | time |
|---|---|---|---|---|
| Deeppose | 192*256 | 41.3% | 65% | 2.5ms |
| Heatmap | 192*256 | 67.5% | 93% | 60ms |
| RLE | 192*256 | 67.3% | 90% | 2.5ms |
从上表中,我们可以发现,当引入RLE损失后,AP提升至67.3%与heatmap相近,同时推理时间仍然保持2.5ms。RLE详细讲解请参考。
4.Integral Pose Regression
我们知道Heatmap推理时,是通过argmax来获取特征图中得分最高的索引,但argmax本身不可导。为了解决这个问题,IPR采用了Soft-Argmax方式解码,先用Softmax对概率热图进行归一化,然后用求期望的方式得到预测坐标。我们在deeppose上引入IPR机制,将最后的fc换成conv层,保留backbone最后层的特征尺寸,并对该特征Softmax,利用期望获得预测坐标。这样做的一大好处是,能够将更多的监督信息引入训练中。
我在mmpose上写了IPRhead代码
@HEADS.register_module()
class IntegralPoseRegressionHead(nn.Module):
def __init__(self,
in_channels,
num_joints,
feat_size,
loss_keypoint=None,
out_sigma=False,
debias=False,
train_cfg=None,
test_cfg=None):
super().__init__()
self.in_channels = in_channels
self.num_joints = num_joints
self.loss = build_loss(loss_keypoint)
self.train_cfg = {} if train_cfg is None else train_cfg
self.test_cfg = {} if test_cfg is None else test_cfg
self.out_sigma = out_sigma
self.conv = build_conv_layer(
dict(type='Conv2d'),
in_channels=in_channels,
out_channels=num_joints,
kernel_size=1,
stride=1,
padding=0)
self.size = feat_size
self.wx = torch.arange(0.0, 1.0 * self.size, 1).view([1, self.size]).repeat([self.size, 1]) / self.size
self.wy = torch.arange(0.0, 1.0 * self.size, 1).view([self.size, 1]).repeat([1, self.size]) / self.size
self.wx = nn.Parameter(self.wx, requires_grad=False)
self.wy = nn.Parameter(self.wy, requires_grad=False)
if out_sigma:
self.gap = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(self.in_channels, self.num_joints * 2)
if debias:
self.softmax_fc = nn.Linear(64, 64)
def forward(self, x):
"""Forward function."""
if isinstance(x, (list, tuple)):
assert len(x) == 1, ('DeepPoseRegressionHead only supports '
'single-level feature.')
x = x[0]
featmap = self.conv(x)
s = list(featmap.size())
featmap = featmap.view([s[0], s[1], s[2] * s[3]])
featmap = F.softmax(16 * featmap, dim=2)
featmap = featmap.view([s[0], s[1], s[2], s[3]])
scoremap_x = featmap.mul(self.wx)
scoremap_x = scoremap_x.view([s[0], s[1], s[2] * s[3]])
soft_argmax_x = torch.sum(scoremap_x, dim=2, keepdim=True)
scoremap_y = featmap.mul(self.wy)
scoremap_y = scoremap_y.view([s[0], s[1], s[2] * s[3]])
soft_argmax_y = torch.sum(scoremap_y, dim=2, keepdim=True)
output = torch.cat([soft_argmax_x, soft_argmax_y], dim=-1)
if self.out_sigma:
x = self.gap(x).reshape(x.size(0), -1)
pred_sigma = self.fc(x)
pred_sigma = pred_sigma.reshape(pred_sigma.size(0), self.num_joints, 2)
output = torch.cat([output, pred_sigma], dim=-1)
return output, featmap
我们引入IPR后实际输出的特征与Heatmap方法输出的特征形式类似,Heatmap方法有人造的概率分布即高斯热图,而在deeppose中引入IPR则是将期望作为坐标,并通过坐标GT直接监督的,因此,只要期望接近GT,loss就会降低。这就带来一个问题,我们通过期望获得的预测坐标无法对概率分布进行约束。
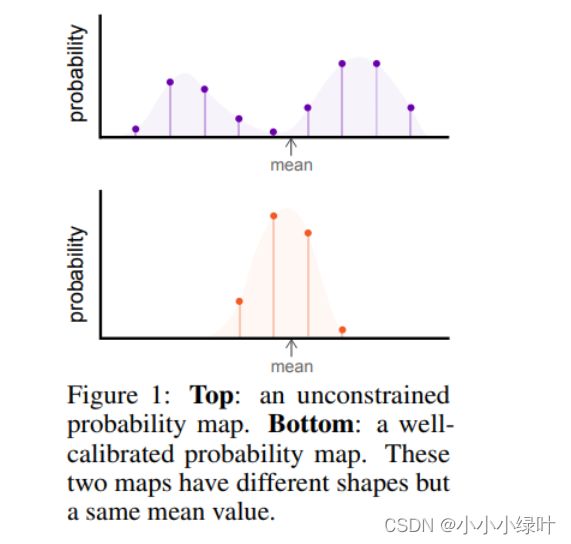
如上图所示,上下两个分布的期望都是mean,但是分布却是完全不同。RLE已经论证一个合理的概率分布是至关重要的,为了提高模型性能,对概率分布加以监督是必要的。DSNT提出了利用JS散度将模型的概率分布向自制的高斯分布靠拢,这里有一个问题,高斯分布的方差只能通过经验值设定,无法针对每个样本自适应的给出,同时高斯分布也未必是最优选择。
@LOSSES.register_module()
class RLE_DSNTLoss(nn.Module):
"""RLE_DSNTLoss loss.
"""
def __init__(self,
use_target_weight=False,
size_average=True,
residual=True,
q_dis='laplace',
sigma=2.0):
super().__init__()
self.dsnt_loss = DSNTLoss(sigma=sigma, use_target_weight=use_target_weight)
self.rle_loss = RLELoss(use_target_weight=use_target_weight,
size_average=size_average,
residual=residual,
q_dis=q_dis)
self.use_target_weight = use_target_weight
def forward(self, output, heatmap, target, target_weight=None):
assert target_weight is not None
loss1 = self.dsnt_loss(heatmap, target, target_weight)
loss2 = self.rle_loss(output, target, target_weight)
loss = loss1 + loss2 # 这里权重可以调参
return loss
@LOSSES.register_module()
class DSNTLoss(nn.Module):
def __init__(self,
sigma,
use_target_weight=False,
size_average=True,
):
super(DSNTLoss, self).__init__()
self.use_target_weight = use_target_weight
self.sigma = sigma
self.size_average = size_average
def forward(self, heatmap, target, target_weight=None):
"""Forward function.
Note:
- batch_size: N
- num_keypoints: K
- dimension of keypoints: D (D=2 or D=3)
Args:
output (torch.Tensor[N, K, D*2]): Output regression,
including coords and sigmas.
target (torch.Tensor[N, K, D]): Target regression.
target_weight (torch.Tensor[N, K, D]):
Weights across different joint types.
"""
loss = dsntnn.js_reg_losses(heatmap, target, self.sigma)
if self.size_average:
loss /= len(loss)
return loss.sum()
从下表可以看出,引入IPR+DSNT后模型性能提升。
| 方法 | input size | AP50:95 | acc_pse | time |
|---|---|---|---|---|
| Deeppose | 192*256 | 41.3% | 65% | 2.5ms |
| Heatmap | 192*256 | 67.5% | 93% | 60ms |
| RLE | 192*256 | 67.3% | 90% | 2.5ms |
| RLE+IPR+DSNT | 256*256 | 70.2% | 95% | 3.5ms |
5.Removing the Bias of Integral Pose Regression
我们引入IPR后,可以使用Softmax来计算期望获得坐标值,但是,利用Softmax计算期望会引入误差。因为Softmax有一个特性让每一项值都非零。对于一个本身非常尖锐的分布,Softmax会将其软化,变成一个渐变的分布。这个性质导致的结果是,最后计算得到的期望值会不准确。只有响应值足够大,分布足够尖锐的时候,期望值才接近Argmax结果,一旦响应值小,分布平缓,期望值会趋近于中心位置。 这种影响会随着特征尺寸的变大而更剧烈。
Removing the Bias of Integral Pose Regression提出debias方法消除Softmax软化产生的影响。具体而言,假设响应值是符合高斯分布的,我们可以根据响应最大值点两倍的宽度,把特征图划分成四个区域:

我们知道一旦经过Softmax,原本都是0值的2、3、4象限区域瞬间就会被长长的尾巴填满,而对于第1象限区域,由于响应值正处于区域的中央,因此不论响应值大小,该区域的估计期望值都会是准确的。
让我们回到Softmax公式:
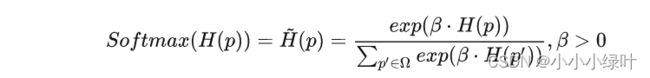
为了简洁,我们先把分母部分用C来表示:
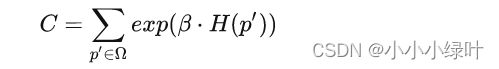
由于假设2、3、4区域的响应值都为0,因而分子部分计算出来为1,划分区域后的Softmax结果可以表示成:
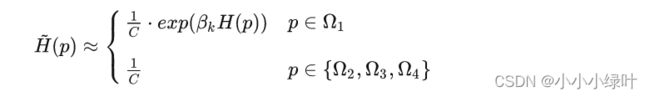
然后继续按照Soft-Argmax的计算公式带入,期望值的计算可以表示为:
即:第一区域的期望值,加上另外三个区域的期望值。已知2,3,4趋于 H ~ ( P ) = 1 / c \tilde{H}(P)=1/c H~(P)=1/c,因此这三个区域的期望值可以把1/c提出来,只剩下
而这里的求和,在几何意义上等价于该区域的中心点坐标乘以该区域的面积,我给一个简单的演示,对于[n, m]区间:
因而对于整块特征图的期望值,又可以看成四个区域中心点坐标的加权和:
由于四个区域的中心点存在对称性,假设第一区域中心点坐标为 J 1 = ( x 0 , y 0 ) J_1=(x_0,y_0) J1=(x0,y0),那么剩下三个区域中心点坐标为 J 2 = ( x 0 , y 0 + w / 2 ) , J 3 = ( x 0 + h / 2 , y 0 ) , J 4 = ( x 0 + h / 2 , y 0 + w / 2 ) J_2=(x_0,y_0+w/2),J_3=(x_0+h/2,y_0), J_4=(x_0+h/2,y_0+w/2) J2=(x0,y0+w/2),J3=(x0+h/2,y0),J4=(x0+h/2,y0+w/2)
对应上面我们得出的1/c乘以中心点坐标乘以面积,就得到了每个加权值:
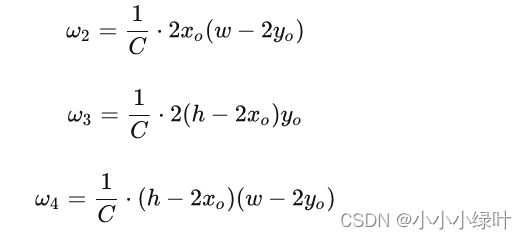
带入上面的加权和公式(6),整张特征图的期望值可以表示为:

由于已知四个区域权重相加为1,所以有 w 1 = 1 − w 2 − w 3 − w 4 w_1=1-w_2-w_3-w_4 w1=1−w2−w3−w4,因此整张特征图期望值化简成如下形式:
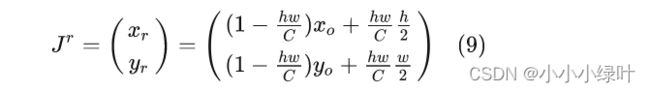
由于 J r J^r Jr值可以很容易通过对整张图计算Soft-Argmax得到,因此对公式(9)移项就能得到准确的第一区域中心点坐标:
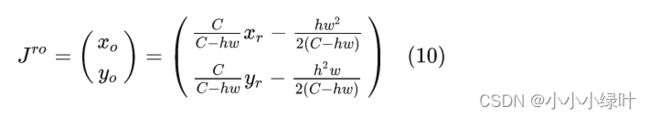
这一步就相当于将原本多余的长尾从期望值中减去了,对该公式我们还可以进一步分析,整张图的期望估计值相当于第一区域期望值的一个偏移。
@HEADS.register_module()
class IntegralPoseRegressionHead(nn.Module):
def __init__(self,
in_channels,
num_joints,
feat_size,
loss_keypoint=None,
out_sigma=False,
debias=False,
train_cfg=None,
test_cfg=None):
super().__init__()
self.in_channels = in_channels
self.num_joints = num_joints
self.loss = build_loss(loss_keypoint)
self.train_cfg = {} if train_cfg is None else train_cfg
self.test_cfg = {} if test_cfg is None else test_cfg
self.out_sigma = out_sigma
self.debias = debias
self.conv = build_conv_layer(
dict(type='Conv2d'),
in_channels=in_channels,
out_channels=num_joints,
kernel_size=1,
stride=1,
padding=0)
self.size = feat_size
self.wx = torch.arange(0.0, 1.0 * self.size, 1).view([1, self.size]).repeat([self.size, 1]) / self.size
self.wy = torch.arange(0.0, 1.0 * self.size, 1).view([self.size, 1]).repeat([1, self.size]) / self.size
self.wx = nn.Parameter(self.wx, requires_grad=False)
self.wy = nn.Parameter(self.wy, requires_grad=False)
if out_sigma:
self.gap = nn.AdaptiveAvgPool2d((1, 1))
self.fc = nn.Linear(self.in_channels, self.num_joints * 2)
if debias:
self.softmax_fc = nn.Linear(64, 64)
def forward(self, x):
"""Forward function."""
if isinstance(x, (list, tuple)):
assert len(x) == 1, ('DeepPoseRegressionHead only supports '
'single-level feature.')
x = x[0]
featmap = self.conv(x)
s = list(featmap.size())
featmap = featmap.view([s[0], s[1], s[2] * s[3]])
if self.debias:
mlp_x_norm = torch.norm(self.softmax_fc.weight, dim=-1)
norm_feat = torch.norm(featmap, dim=-1, keepdim=True)
featmap = self.softmax_fc(featmap)
featmap /= norm_feat
featmap /= mlp_x_norm.reshape(1, 1, -1)
featmap = F.softmax(16 * featmap, dim=2)
featmap = featmap.view([s[0], s[1], s[2], s[3]])
scoremap_x = featmap.mul(self.wx)
scoremap_x = scoremap_x.view([s[0], s[1], s[2] * s[3]])
soft_argmax_x = torch.sum(scoremap_x, dim=2, keepdim=True)
scoremap_y = featmap.mul(self.wy)
scoremap_y = scoremap_y.view([s[0], s[1], s[2] * s[3]])
soft_argmax_y = torch.sum(scoremap_y, dim=2, keepdim=True)
# output = torch.cat([soft_argmax_x, soft_argmax_y], dim=-1)
if self.debias:
C = featmap.reshape(s[0], s[1], s[2] * s[3]).exp().sum(dim=2).unsqueeze(dim=2)
soft_argmax_x = C / (C - 1) * (soft_argmax_x - 1 / (2 * C))
soft_argmax_y = C / (C - 1) * (soft_argmax_y - 1 / (2 * C))
output = torch.cat([soft_argmax_x, soft_argmax_y], dim=-1)
if self.out_sigma:
x = self.gap(x).reshape(x.size(0), -1)
pred_sigma = self.fc(x)
pred_sigma = pred_sigma.reshape(pred_sigma.size(0), self.num_joints, 2)
output = torch.cat([output, pred_sigma], dim=-1)
return output, featmap
| 方法 | input size | AP50:95 | acc_pse | time |
|---|---|---|---|---|
| Deeppose | 192*256 | 41.3% | 65% | 2.5ms |
| Heatmap | 192*256 | 67.5% | 93% | 60ms |
| RLE | 192*256 | 67.3% | 90% | 2.5ms |
| RLE+IPR+DSNT | 256*256 | 70.2% | 95% | 3.5ms |
| RLE+IPR+DSNT+debias | 256*256 | 71% | 95% | 3.5ms |
非常感谢知乎作者镜子文章给予的指导,在这里借鉴了很多,有兴趣的朋友可以查看知乎地址。