图书销量时间序列预测_数学建模_Prophet实现

前言

• 该题来源于数学建模校内选拔赛，给出了简单的数据，恰好我找到prophet这个神器，便用它来完成题目了，一开始只打算来做做第一题预测什么的，结果做着做着居然发现能只靠prophet库把每个小问给圆上。原来时间紧张代码写得东一块西一块，现在有时间了稍微整理了下代码发了上来。

• 说一下对prophet的使用感受。这模型还是非常强的，原理也不难，搞清楚使用后几行代码就能把预测图和时间序列分解图画出来，非常适合需要马上上手预测的任务。虽然给出的可调参数不少，不过需要调整的并不多，像是什么初始影响因子的值的，调了下感觉无论初始设置多少，训练的时候都会很快收敛到相同的解，不过也许是因为我的数据集比较简单。

• 比赛任务一要求对销售数据进行建模预测和模型评估，任务二要求寻求与销量走势相关的其他属性，任务三要求寻分析导致销量量骤升骤降的原因并用于修正原模型。

• 使用prophet解决思路也很简单，不过因为题目给的数据只有2年内逐月的数据，总共24个观察值，采样点太少，可能没法发挥出prophet的真实力量。

• 任务一预测已经是库里面自带的了，评估的话就把数据归一化后计算其预测误差就好；任务二的话，把prophet训练得到的趋势项在变点上的斜率提取出来和周期项的傅里叶展开系数结合起来作为特征，用层次聚类聚集出几个簇，找到类内和类均值比总误差较小的几类就得到走势相同的曲线了，这个任务的完成效果还是不错的；任务三就有点勉强了，大概思路是把对每个样本把骤升骤降的点标记处理，让prophet增加一个残差回归项去学习这些骤变情况（这部分感觉理解不是很到位）。

• 许久后回头看看这份代码建模报告, 感觉也没写啥(捂脸 , 好在校内选拔赛是能过了的

主要参考

• 主要参考的即为github上的发布连接 https://github.com/facebook/prophet

代码

库导入与函数设置

导库

import numpy as np
import pandas as pd
import matplotlib.pylab as plt
import seaborn as sns
from itertools import cycle
from fbprophet import Prophet # 0.7版本
from fbprophet.plot import add_changepoints_to_plot
import copy as cp
import datetime 
import time
import random

pd.set_option('max_columns', 50)
plt.style.use('bmh')
color_pal = plt.rcParams['axes.prop_cycle'].by_key()['color']
color_cycle = cycle(plt.rcParams['axes.prop_cycle'].by_key()['color'])

# 忽略警告
import warnings
warnings.filterwarnings('ignore')

# 绘制更清晰的图片
%config InlineBackend.figure_format = 'svg'

# 设置图片内的中文与负号显示
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False

import os

INPUT_DIR = os.path.realpath('.')

展示函数

def ShowBiog(data,data_index):
#  展示商品的销售曲线
#  data是数据集，data_index是 索引号
    plt.figure(figsize=(10, 3))
    ax = fig.add_subplot(111)

    example = data.iloc[data_index]
    # 由于是完整的数据集中带有商品品类、出版时间等非销量数据，需去掉
    example[4:-1].plot(
            color=next(color_cycle),
           )
    plt.title('{}'.format(example['品种']))
#     ax.set_xticklabels('')
#     plt.legend('')
    plt.show()

取数据函数

def GetData(data,data_index):
#  该函数主要负责从data中取出索引号为data_index的数据
#  并生成为prophet能识别的形式
    data = data.drop(data.columns[0:4], axis=1)
    if 'SUM' in data.columns:
        data = data.drop(data.columns[-1], axis=1)
    data = data.T.reset_index()

    data0 = pd.DataFrame([data.iloc[:,0].values,data.iloc[:,data_index+1].values]).T
    data0.rename(columns={0:'ds', 1:'y'},inplace=True)
    return data0

训练函数

def FlagFunc(ds,train):
#  该函数主要是遍历数据，并数据发生骤升骤降时进行标记，用于残差回归
#  参数train表示作为训练数据的天数，超过该天数的数据标记为0
    tem = list()
    for i in range(ds.shape[0]): 
        if i in [0,1]:  # 前两项默认标识为0
            tem.append(0)
        elif i not in range(train):  #  为非训练数据，记0
            tem.append(0)
        #  骤升骤降的判断标准设定为相对两天前，今天的增/减量超过两天前的40%
        elif (ds['y'][i] - ds['y'][i-2]) > 0.4 * ds['y'][i-2]:  # 骤升，记1
            tem.append(1) 
        elif -(ds['y'][i] - ds['y'][i-2]) > 0.4 * ds['y'][i-2]:  # 骤降，记-1
            tem.append(-1)
        else:  # 正常情况，记0
            tem.append(0)
    return tem

def Fit(data0,
        train=24,periods=6,  #  训练天数以及预测天数
        m=None,holidays=None,
        predict=True,Draw=True,  #  标记是否进行预测和绘图
        length=8,width=4,  # 绘图时代图片尺寸
        Reg=False,  #  是否使用残差回归项
       ):
#     data = pd.read_csv(f'{INPUT_DIR}/Data.csv')
    if holidays==None:   # 若为指定holiday数据，则生成
    #  这里设定为每年元旦、3月开学、6月中、8月中、9月开学、双十一，影响周期为后15天
        holidays = pd.DataFrame({
          'holiday': 'Promotion',
          'ds': pd.to_datetime(['2019-01-01','2019-03-01','2019-06-15',
                               '2019-08-15','2019-09-01','2019-11-11',
                               '2020-01-01','2020-03-01','2020-06-15',
                               '2020-08-15','2020-09-01','2020-11-11',
                               '2021-01-01','2021-03-01','2021-06-15',
                               '2021-08-15','2021-09-01','2021-11-11',]),
          'lower_window': 0,
          'upper_window': 15,
        })
    #  未指定训练模型则创建
    if m==None:
        m = Prophet(growth='linear',
                    holidays=holidays,holidays_prior_scale=10,
                    n_changepoints=5,changepoint_range=0.9,changepoint_prior_scale=0.5,
                    daily_seasonality=False,weekly_seasonality=False,yearly_seasonality=False)
        #  趋势项使用分段线性模型，5个变点，均匀分布在前90%数据上，其初始影响强度为0.5
        m.add_seasonality(name='yearly', period=365.25, fourier_order=3,prior_scale=10)
        #  加入年周期项，周期为365.25，傅立叶展开到第3项，初始影响强度为默认值10
    if Reg:
    	# 若使用残差回归项，则给data0再增添一列'reg'项，其值由前面定义的Flagfunc函数定义
        data0['reg'] = pd.Series(FlagFunc(data0,train), index=data0.index)
        #  在模型中加入残差回归项，初始影响强度为默认值10
        m.add_regressor('reg',prior_scale=10)
    # 训练指定天数的数据
    m.fit(data0[:train])
    
    if predict==True:
    	# 若需进行预测，在原训练天数时间列表后增添预测的天数
    	# freq表示生成的时间是按月生成的
        future = m.make_future_dataframe(periods=periods,freq='BM')
        if Reg:
        	# 生成的future时间列表也需要有'reg'项，这里和上面作同样处理
            future['reg'] = pd.Series(FlagFunc(future,train), index=future.index)
        forecast = m.predict(future)

    else:
        return m

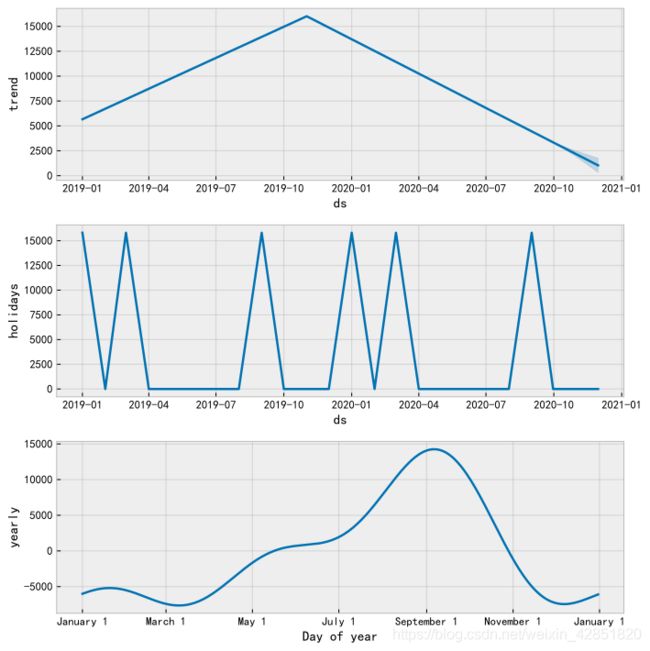
    if Draw:
    	# 绘制拟合图
        fig = m.plot(forecast,figsize=(length, width))
        x1 = forecast['ds']
        y2 = forecast['yhat_lower']
        y3 = forecast['yhat_upper']
        # 绘制预测区间的上下界
        plt.plot(x1,y2,alpha=0.3)
        plt.plot(x1,y3,alpha=0.3)
        #  预测情况也绘制进去
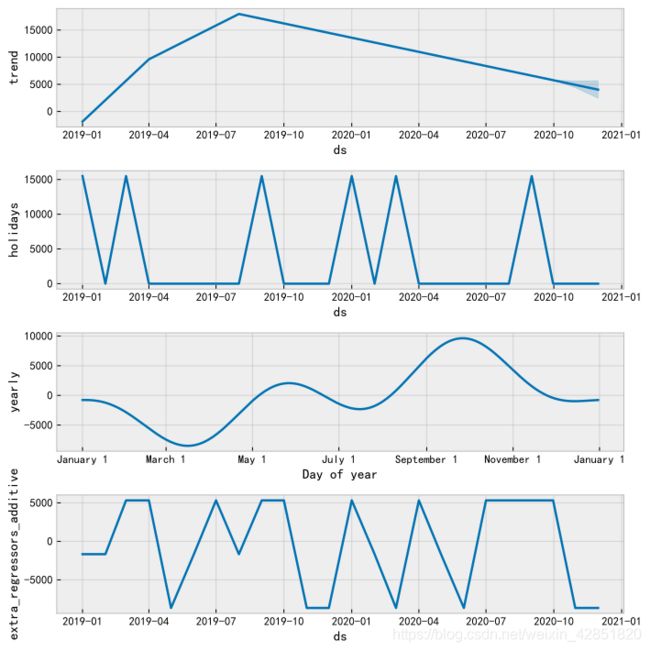
        m.plot_components(forecast,figsize=(length, width*2))
		# 绘制趋势项和变点位置
        a = add_changepoints_to_plot(fig.gca(), m, forecast)
        plt.show()
        return fig
    else:
        return forecast

评估函数

def Estimate(data,train=21,periods=3,Reg=False):
#  在data数据集上使用MAE指标进行评估
# train是训练天数，periods为预测天数
    preds = pd.DataFrame(columns=range(periods))
    trues = pd.DataFrame(columns=range(periods))

    start_time = time.time()

    for SI in range(data.shape[0]):

        data0 = GetData(data,SI)
        # 统一量级，需要对数据进行归一化
        data0['y'] = (data0['y'] - data0['y'].min()) / (data0['y'].max() - data0['y'].min())
        data0
        
        forecast = Fit(data0,train=train,periods=periods,predict=True,Draw=False,Reg=Reg)
		# 若预测值小于0，则记为0
        preds.loc[SI] = [int(x) if x > 0 else 0 for x in forecast['yhat'][-periods:].values]
        trues.loc[SI] = data0[-periods:]['y'].values

        if ((SI+1) % 50 == 0):
#             if SI==0 : continue
            print("第{:0>4d}个样本处理完毕，耗时 {:.4f}s".format(int(SI)+1,time.time()-start_time))
            start_time = time.time()
	# 返回MAE
    return ((preds - trues).abs() / preds.shape[0]).sum()

数据预处理

OriginalData = pd.read_excel(f'{INPUT_DIR}/少儿.xlsx')
# OriginalData = pd.read_excel(f'{INPUT_DIR}/传记.xlsx')
OriginalData.head(5)

	品种	出版时间	出版社	作者	2019-01-01 00:00:00	2019-02-01 00:00:00	2019-03-01 00:00:00	2019-04-01 00:00:00	2019-05-01 00:00:00	2019-06-01 00:00:00	2019-07-01 00:00:00	2019-08-01 00:00:00	2019-09-01 00:00:00	2019-10-01 00:00:00	2019-11-01 00:00:00	2019-12-01 00:00:00	2020-01-01 00:00:00	2020-02-01 00:00:00	2020-03-01 00:00:00	2020-04-01 00:00:00	2020-05-01 00:00:00	2020-06-01 00:00:00	2020-07-01 00:00:00	2020-08-01 00:00:00	2020-09-01 00:00:00	2020-10-01 00:00:00	2020-11-01 00:00:00	2020-12-01 00:00:00
0	1924873_小猪唏哩呼噜(aoe名著注音版下)	2008-06-01 00:00:00	408_春风文艺	195_孙幼军	1358.0	5003.0	18055.0	8828.0	5837.0	9924.0	24219.0	13388.0	47861.0	23966.0	14824.0	5727.0	39560.0	6044.0	8435.0	8658.0	5073.0	3751.0	12158.0	7530.0	37444.0	13772.0	9334.0	3872.0
1	1362380_小布头奇遇记(aoe名著注音版)	2008-03-01 00:00:00	408_春风文艺	195_孙幼军	2293.0	313.0	925.0	518.0	466.0	831.0	1229.0	266.0	736.0	481.0	195.0	93.0	758.0	177.0	367.0	574.0	244.0	254.0	884.0	211.0	580.0	206.0	244.0	220.0
2	1924872_小猪唏哩呼噜(aoe名著注音版上)	2008-03-01 00:00:00	408_春风文艺	195_孙幼军	1468.0	5046.0	18107.0	8852.0	5858.0	9971.0	24222.0	13332.0	47798.0	24060.0	14885.0	5701.0	39452.0	6057.0	8417.0	8639.0	5066.0	3749.0	12219.0	7569.0	37674.0	13988.0	9364.0	3888.0
3	507595_毛毛(时间窃贼和一个小女孩的不可思议的故事)/幻想文学大师书系	2009-03-01 00:00:00	426_二十一世纪	2114_米切尔·恩德	2442.0	1104.0	1022.0	776.0	656.0	1477.0	3635.0	1120.0	2804.0	1068.0	1762.0	993.0	5061.0	688.0	1070.0	763.0	429.0	546.0	7765.0	1671.0	2229.0	915.0	1518.0	964.0
4	1910267_和乌鸦做邻居/动物小说大王沈石溪品藏书系	2008-11-01 00:00:00	231_浙江少儿	67319_沈石溪	394.0	102.0	156.0	78.0	86.0	285.0	159.0	49.0	64.0	144.0	82.0	51.0	106.0	24.0	47.0	75.0	60.0	62.0	111.0	42.0	44.0	22.0	71.0	87.0

OriginalData.shape

(20006, 28)

# OriginalData.info()

# 查看缺失信息
OriginalData.isnull().sum()

品种                      5
出版时间                   87
出版社                     1
作者                      1
2019-01-01 00:00:00     6
2019-02-01 00:00:00     6
2019-03-01 00:00:00     6
2019-04-01 00:00:00     6
2019-05-01 00:00:00     6
2019-06-01 00:00:00     6
2019-07-01 00:00:00     6
2019-08-01 00:00:00     6
2019-09-01 00:00:00     6
2019-10-01 00:00:00     6
2019-11-01 00:00:00     6
2019-12-01 00:00:00     6
2020-01-01 00:00:00     6
2020-02-01 00:00:00     6
2020-03-01 00:00:00     6
2020-04-01 00:00:00     6
2020-05-01 00:00:00     6
2020-06-01 00:00:00     6
2020-07-01 00:00:00     6
2020-08-01 00:00:00     6
2020-09-01 00:00:00     6
2020-10-01 00:00:00    11
2020-11-01 00:00:00    11
2020-12-01 00:00:00    11
dtype: int64

# 查看销售量为负值或空值的行
OriginalData[~(OriginalData.iloc[:,-24:] >= 0).all(axis=1)]

	品种	出版时间	出版社	作者	2019-01-01 00:00:00	2019-02-01 00:00:00	2019-03-01 00:00:00	2019-04-01 00:00:00	2019-05-01 00:00:00	2019-06-01 00:00:00	2019-07-01 00:00:00	2019-08-01 00:00:00	2019-09-01 00:00:00	2019-10-01 00:00:00	2019-11-01 00:00:00	2019-12-01 00:00:00	2020-01-01 00:00:00	2020-02-01 00:00:00	2020-03-01 00:00:00	2020-04-01 00:00:00	2020-05-01 00:00:00	2020-06-01 00:00:00	2020-07-01 00:00:00	2020-08-01 00:00:00	2020-09-01 00:00:00	2020-10-01 00:00:00	2020-11-01 00:00:00	2020-12-01 00:00:00
5721	1724091_盖房子(幼儿版)(精)/妙趣科学立体书	2014-09-01 00:00:00	65_北京科技	745145_克斯廷·舒尔德	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
5722	NaN	8	9	6	5.0	5.0	4.0	7.0	17.0	6.0	2.0	7.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	NaN	NaN	NaN
14366	2435466_小达尔文自然科学馆套装（共4册）	2017-06-28 00:00:00	125_中国妇女	795956_查尔斯·达尔文	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
14367	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
14368	NaN	17	12	27	17.0	16.0	16.0	21.0	13.0	29.0	7.0	18.0	4.0	1.0	0.0	0.0	0.0	0.0	4.0	2.0	2.0	1.0	1.0	0.0	1.0	NaN	NaN	NaN
15749	1724785_草丛中的奥秘(幼儿版)(精)/妙趣科学立体书	2014-09-01 00:00:00	65_北京科技	745179_伊姆加德·埃伯哈德	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
15750	NaN	4	3	4	6.0	6.0	6.0	7.0	8.0	2.0	1.0	1.0	5.0	1.0	4.0	5.0	5.0	1.0	8.0	0.0	0.0	0.0	0.0	0.0	2.0	NaN	NaN	NaN
16098	2424736_欢乐农场日(中英双语韵文)/小熊很忙	2016-07-01 00:00:00	99_中信	795707_	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
16099	本吉·戴维斯	92	6	0	0.0	8.0	0.0	0.0	0.0	0.0	0.0	0.0	2.0	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	NaN	NaN	NaN
17263	1724123_非洲动物(幼儿版)(精)/妙趣科学立体书	2014-09-01 00:00:00	65_北京科技	745147_达妮埃拉·普鲁斯	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
17264	NaN	3	7	12	8.0	6.0	6.0	4.0	6.0	3.0	4.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	NaN	NaN	NaN

# 查看品种为空值的行
OriginalData[OriginalData.iloc[:,0].isnull()]

	品种	出版时间	出版社	作者	2019-01-01 00:00:00	2019-02-01 00:00:00	2019-03-01 00:00:00	2019-04-01 00:00:00	2019-05-01 00:00:00	2019-06-01 00:00:00	2019-07-01 00:00:00	2019-08-01 00:00:00	2019-09-01 00:00:00	2019-10-01 00:00:00	2019-11-01 00:00:00	2019-12-01 00:00:00	2020-01-01 00:00:00	2020-02-01 00:00:00	2020-03-01 00:00:00	2020-04-01 00:00:00	2020-05-01 00:00:00	2020-06-01 00:00:00	2020-07-01 00:00:00	2020-08-01 00:00:00	2020-09-01 00:00:00	2020-10-01 00:00:00	2020-11-01 00:00:00	2020-12-01 00:00:00
5722	NaN	8	9	6	5.0	5.0	4.0	7.0	17.0	6.0	2.0	7.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	NaN	NaN	NaN
14367	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN	NaN
14368	NaN	17	12	27	17.0	16.0	16.0	21.0	13.0	29.0	7.0	18.0	4.0	1.0	0.0	0.0	0.0	0.0	4.0	2.0	2.0	1.0	1.0	0.0	1.0	NaN	NaN	NaN
15750	NaN	4	3	4	6.0	6.0	6.0	7.0	8.0	2.0	1.0	1.0	5.0	1.0	4.0	5.0	5.0	1.0	8.0	0.0	0.0	0.0	0.0	0.0	2.0	NaN	NaN	NaN
17264	NaN	3	7	12	8.0	6.0	6.0	4.0	6.0	3.0	4.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	NaN	NaN	NaN

# # 查看出版时间属性不正确的行
# OriginalData[OriginalData.iloc[:,1].apply(lambda x: type(x)!=datetime.datetime)]

#  清除异常数据
Clean_flag = (~OriginalData.iloc[:,0].isnull()) & ((OriginalData.iloc[:,-24:] >= 0).all(axis=1)) 
#             & (~OriginalData.iloc[:,1].apply(lambda x: type(x)!=datetime.datetime))
CleanData = OriginalData[Clean_flag]

CleanData.shape

(19995, 28)

数据集划分

By20190101 = datetime.datetime.strptime('2019-01-01','%Y-%m-%d')

# 查看在2019.01.01前出版的图书数量
DataBf20190101 = CleanData[CleanData['出版时间'].apply(lambda x: pd.to_datetime(x)) 
                              < By20190101]
DataAf20190101 = CleanData[CleanData['出版时间'].apply(lambda x: pd.to_datetime(x)) 
                              >= By20190101]

print(DataBf20190101.shape[0])
print(DataAf20190101.shape[0])

19169
740

# DataBf20190101.to_csv(f'{INPUT_DIR}/DataBf2019.csv', index=False);
# DataAf20190101.to_csv(f'{INPUT_DIR}/DataAf2019.csv', index=False);

数据分布查看

Data = cp.deepcopy(DataBf20190101)

Data['SUM'] = Data.drop(Data.columns[0:4], axis=1).apply(lambda x: x.sum(), axis=1)

Data['SUM'].describe()

count     19169.000000
mean       1472.592780
std        9089.342682
min           0.000000
25%           8.000000
50%          68.000000
75%         360.000000
max      335382.000000
Name: SUM, dtype: float64

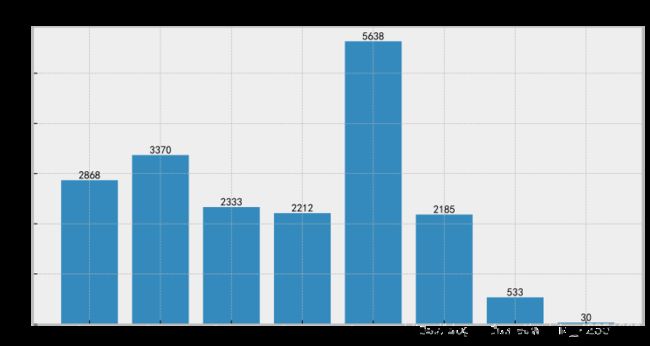
region = [0,1,20,50,100,1e3,1e4,1e5,1e6]
region_str = ['0','1','20','50','100','1e3','1e4','1e5','无穷']
y = []
for i in range(len(region)-1):
    y.append(np.sum((Data['SUM']>=region[i]) & (Data['SUM']<region[i+1])))

fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(111)
rects = ax.bar(range(len(region)-1),y)

for rect in rects: 
    height = rect.get_height()
    plt.text(rect.get_x() + rect.get_width() / 2, height, str(height)\
             , size=10, ha='center', va='bottom')

ax.set_xticklabels(['[{},{})'.format(region_str[i-1],region_str[i]) for i in range(len(region))])
plt.title('累计销量频数分布')
# plt.savefig('./累计销量频数分布',dpi=400)
plt.show()

# 箱线图，暂时用不上
# fig = plt.figure(figsize=(8, 8))

# ax = fig.add_subplot(121)
# ax.boxplot(np.log(Data['SUM'][Data['SUM']>=100].values)/np.log(10),
#             flierprops = {'marker':'o','markerfacecolor':'pink'},
#            )  
# ax.set_ylabel('log10')
# ax.set_title('总销量大于等于200的书籍')

# ax = fig.add_subplot(122)
# ax.boxplot(Data['SUM']
#                    [(Data['SUM'].values>1)&(Data['SUM'].values<100)].values,
#             flierprops = {'marker':'o','markerfacecolor':'pink'}
#             )
# ax.set_ylabel('')
# ax.set_title('总销量大于1小于200的书籍')
# # plt.savefig('./BiogDescribe.jpg',dpi=400)
# plt.show()

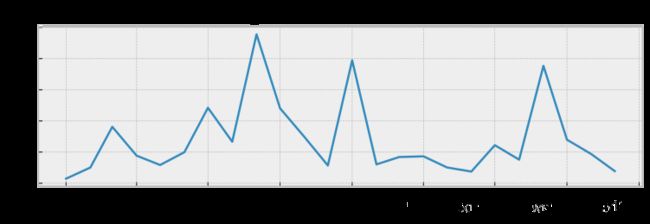
销售曲线查看

ShowBiog(Data,2)

销售预测

# %matplotlib auto
# %matplotlib inline

data_index = 2

train = 21
periods = 3

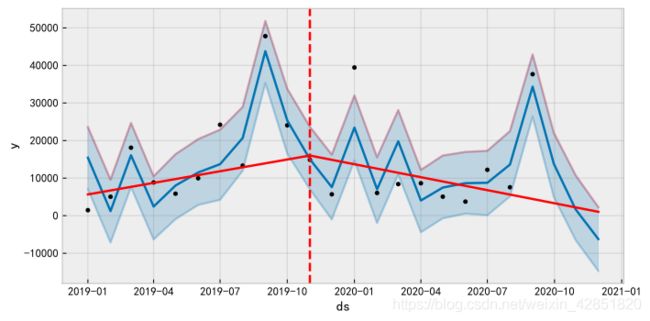
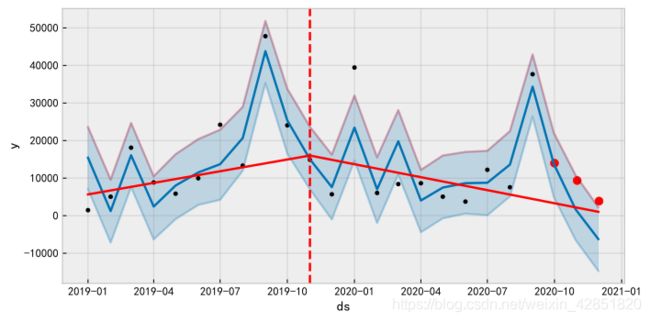
pic = Fit(GetData(Data,data_index),train=train,periods=periods,predict=True,Draw=True)

​

# 把真实值也绘进图内
if pic!=None:
    ax = pic.add_subplot(111)
    ax.scatter(Data.iloc[data_index][-periods-1:-1].index,\
               Data.iloc[data_index][-periods-1:-1].values,s=50,c='r')
pic

​

误差分析

Data1e4 = Data[Data['SUM'] >= 1e4]

random.seed(0)

Data1 = Data[Data['SUM'] >= 1e4].sample(100)
Data1.shape

(100, 29)

Data2 = Data[(Data['SUM'] >= 1e3)&(Data['SUM'] < 1e4)].sample(100)
Data2.shape

(100, 29)

Data3 = Data[(Data['SUM'] >= 1e2)&(Data['SUM'] < 1e3)].sample(100)
Data3.shape

(100, 29)

# 三种销量规模的数据随机取100条，评估MAE
MAE_1 = Estimate(Data1,train=18,periods=6)
MAE_2 = Estimate(Data2,train=18,periods=6)
MAE_3 = Estimate(Data3,train=18,periods=6)

第0050个样本处理完毕，耗时 53.8408s
第0100个样本处理完毕，耗时 53.6914s
第0050个样本处理完毕，耗时 53.6740s
第0100个样本处理完毕，耗时 55.2016s
第0050个样本处理完毕，耗时 53.0966s
第0100个样本处理完毕，耗时 53.5304s

plt.plot(MAE_1)
plt.plot(MAE_2)
plt.plot(MAE_3)
plt.legend(['[1e4,)','[1e3,1e4)','[1e2,1e3)'])
plt.show()

​

聚类分析

# Data1e4 = Data[Data['SUM'] > 1e4]

train = 24
periods = 0
# 保存特征
Features = pd.DataFrame(columns=(['trend{}'.format(i) for i in range(6)]
                           + ['beta{}'.format(i) for i in range(7)]
                  ))

start_time = time.time()

for SI in range(Data1e4.shape[0]):

    data0 = GetData(Data1e4,SI)
    m = Fit(data0,train=train,periods=periods,predict=False)

    params = m.params
    k_values = list(params['k'][0])
    m_values = params['m'][0].tolist()
	# 计算在各变点处的趋势项斜率
    for i in range(m.params['delta'].shape[1]):
        k_values.append(k_values[-1] + params['delta'][0][i])
	# 把6个趋势项斜率信息和7个傅立叶展开系数作为特征值保存
    Features.loc[SI] = list(k_values[:6]) + list(params['beta'][0][:7]) 
    
    if (SI+1) % 50 == 0:
        print("第{:0>4d}个样本处理完毕，耗时 {:.4f}s".format(int(SI)+1,time.time()-start_time))
        start_time = time.time()

第0050个样本处理完毕，耗时 7.6109s
第0100个样本处理完毕，耗时 7.7539s
第0150个样本处理完毕，耗时 7.6524s
第0200个样本处理完毕，耗时 7.5766s
第0250个样本处理完毕，耗时 7.9535s
第0300个样本处理完毕，耗时 8.2524s
第0350个样本处理完毕，耗时 8.1912s
第0400个样本处理完毕，耗时 8.1910s
第0450个样本处理完毕，耗时 8.0806s
第0500个样本处理完毕，耗时 8.1062s
第0550个样本处理完毕，耗时 8.7124s

# Features.head()

from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn.cluster import AgglomerativeClustering as AC
from collections import Counter

# 绘制层次聚类树，在样本过多情况下视觉效果并不好
# plt.figure(figsize=(20,5))

# Z = linkage(Features.values, method='ward', metric='euclidean')

# p = dendrogram(Z, 0)
# plt.title('累计销量大于10000的书籍的层次聚类树')
# # plt.savefig('./ACTree.jpg',dpi=400)
# plt.show()

#  使用层次聚类分为100类
n_clusters = 100

model = AC(n_clusters=n_clusters,linkage='ward',compute_full_tree='auto')
y = model.fit_predict(Features.values)

Clusters = {cluster:[i for i,c in enumerate(y) if c==cluster] for cluster in range(n_clusters)}

SimilarClusters = pd.DataFrame(columns=['MAE','cnt'])
# 计算每个聚类簇内的MAE和样本数
for ID in Clusters:

    df = Data1e4.iloc[Clusters[ID],4:-1].T
    df = (df-df.min())/(df.max()-df.min())
    cnt = len(Clusters[ID])
    mae = (df.T-df.mean(axis=1)).abs().sum().sum() / cnt
    SimilarClusters.loc[ID]=[mae,cnt]

# 依据MAE升序排序
SimilarClusters = SimilarClusters[SimilarClusters['cnt']!=1].sort_values(by='MAE')
SimilarClusters.head(10)

	MAE	cnt
25	0.289307	2.0
62	0.309397	5.0
97	0.455214	7.0
18	0.603420	2.0
69	0.619963	3.0
89	0.894594	5.0
94	1.013181	2.0
32	1.062851	4.0
28	1.429701	3.0
75	1.554918	2.0

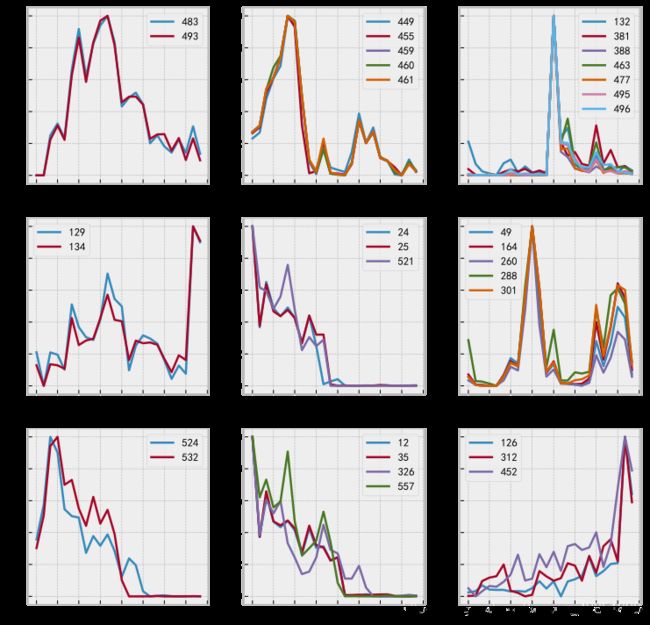
#  展示MAE前9小的簇的曲线走势
fig = plt.figure(figsize=(10,10))
for i in range(9):
    ax = fig.add_subplot(3,3,i+1)
    ClusterID = SimilarClusters.index[i]
    df = Data1e4.iloc[Clusters[ClusterID],4:-1].T
    ax.plot(((df-df.min())/(df.max()-df.min())))
    ax.legend(Clusters[ClusterID])
    ax.set_xticklabels(range(24))
plt.show()

​

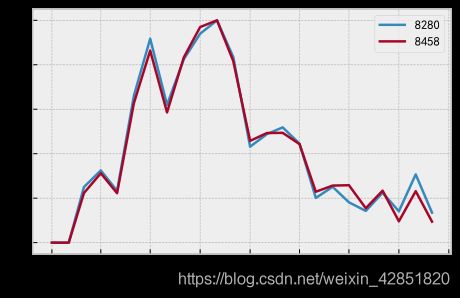
# 查看对应簇内的走势曲线和它们的其他属性信息
ClusterID = SimilarClusters.index[0]
df = Data1e4.iloc[Clusters[ClusterID],4:-1].T
((df-df.min())/(df.max()-df.min())).plot()
plt.show()
Data1e4.iloc[Clusters[ClusterID],[0,1,2,3,-1]]

	品种	出版时间	出版社	作者	SUM
8280	884162_彩图注音版-宋词三百首	2018-07-01 00:00:00	417_哈尔滨	_	11717.0
8458	884163_彩图注音版-唐诗三百首	2018-07-01 00:00:00	417_哈尔滨	_	12146.0

ClusterID = SimilarClusters.index[1]
df = Data1e4.iloc[Clusters[ClusterID],4:-1].T
((df-df.min())/(df.max()-df.min())).plot()
plt.show()
Data1e4.iloc[Clusters[ClusterID],[0,1,2,3,-1]]

​

	品种	出版时间	出版社	作者	SUM
6838	2319048_香喷喷的早饭我要吃(精)	2018-07-01 00:00:00	2073_中国福利会	789895_弥弥	21403.0
7035	1730057_人类的房子(精)	2018-04-01 00:00:00	2073_中国福利会	605423_岑建强	17033.0
7293	2319057_玉米(精)	2018-07-01 00:00:00	2073_中国福利会	790543_郭之武	16813.0
7294	2319059_爱能永恒(精)	2018-07-01 00:00:00	2073_中国福利会	694140_张松奎	16871.0
7295	2319066_芙蓉仙子(精)	2018-08-01 00:00:00	2073_中国福利会	125460_石淼	17165.0

ClusterID = SimilarClusters.index[2]
df = Data1e4.iloc[Clusters[ClusterID],4:-1].T
((df-df.min())/(df.max()-df.min())).plot()
plt.show()
Data1e4.iloc[Clusters[ClusterID],[0,1,2,3,-1]]

​

	品种	出版时间	出版社	作者	SUM
1428	1049548_那年深夏/长青藤国际大奖小说书系	2016-01-01 00:00:00	317_晨光	179598_史蒂夫·克卢格	13881.0
5546	2277329_班长下台	2016-05-01 00:00:00	423_福建少儿	67422_桂文亚	10803.0
5671	2281686_我们的一年级(注音版)	2018-04-01 00:00:00	130_北京联合	233015_童喜喜	28506.0
7321	871679_非凡十二岁/魔法象	2018-06-01 00:00:00	444_广西师大	264544_刘墨语	13732.0
8168	2319980_我们都一样/淘气姐妹花	2018-08-01 00:00:00	231_浙江少儿	150326_子鱼	11744.0
8567	872270_不乖童话/彩虹桥系列桥梁书	2018-05-01 00:00:00	423_福建少儿	206555_右耳	10258.0
8699	2298202_地球的笔记(精)	2018-09-01 00:00:00	444_广西师大	113748_林世仁	12022.0

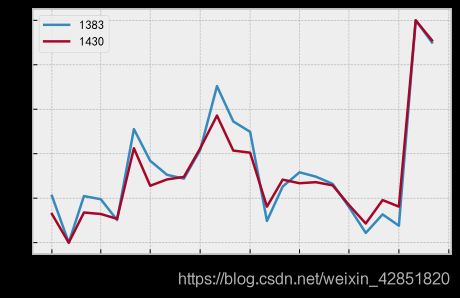
ClusterID = SimilarClusters.index[3]
df = Data1e4.iloc[Clusters[ClusterID],4:-1].T
((df-df.min())/(df.max()-df.min())).plot()
plt.show()
Data1e4.iloc[Clusters[ClusterID],[0,1,2,3,-1]]

	品种	出版时间	出版社	作者	SUM
1383	1108425_典藏国学漫画系列(共6册)	2016-04-01 00:00:00	289_广州	120614_蔡志忠	13371.0
1430	1108426_典藏国学漫画系列(3共6册)	2015-04-01 00:00:00	289_广州	120614_蔡志忠	10309.0

残差拟合

Data1e4 = Data[Data['SUM'] > 1e4]
Data1e4.shape

(563, 29)

data_index = 2

train = 21
periods = 3
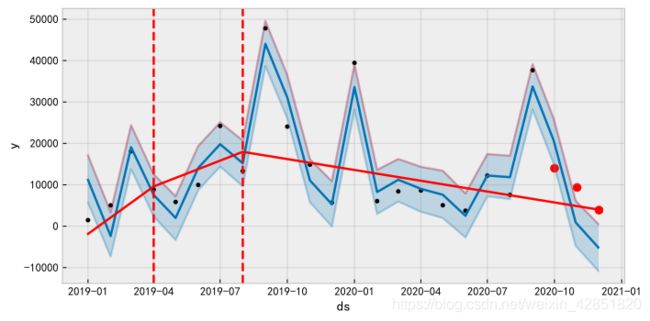
#  对比加入残差回归项前后的拟合曲线图
pic = Fit(GetData(Data,data_index),train=train,periods=periods,predict=True,Draw=True,Reg=True)

if pic!=None:
    ax = pic.add_subplot(111)
    ax.scatter(Data.iloc[data_index][-periods-1:-1].index,\
               Data.iloc[data_index][-periods-1:-1].values,s=50,c='r')
pic

random.seed(0)

DataSample = Data1e4.sample(100)

MAE = Estimate(DataSample,train=18,periods=6,Reg=False)

第0050个样本处理完毕，耗时 56.8565s
第0100个样本处理完毕，耗时 60.1211s

MAE_Reg = Estimate(DataSample,train=18,periods=6,Reg=True)

第0050个样本处理完毕，耗时 58.6181s
第0100个样本处理完毕，耗时 57.4036s

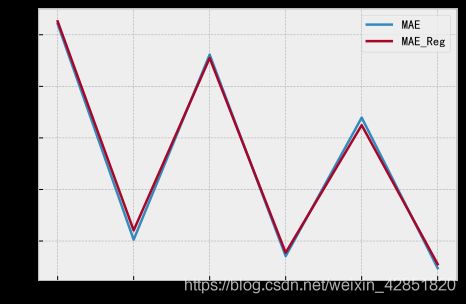
plt.plot(MAE)
plt.plot(MAE_Reg)
plt.legend(['MAE','MAE_Reg'])
plt.show()

​