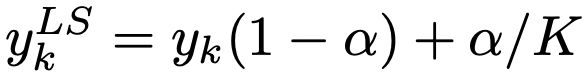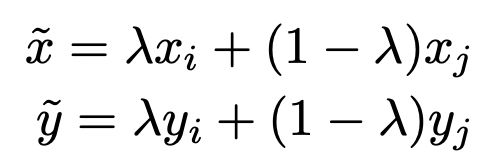模型概率后校验方法
大家在训练深度学习模型的时候,有没有遇到这样的场景:分类任务的准确率比较高,但是模型输出的预测概率和实际预测准确率存在比较大的差异?这就是现代深度学习模型面临的校准问题。在很多场景中,我们不仅关注分类效果或者排序效果(auc),还希望模型预测的概率也是准的。例如在自动驾驶场景中,如果模型无法以置信度较高的水平检测行人或障碍物,就应该通过输出概率反映出来,并让模型依赖其他信息进行决策。再比如在广告场景中,ctr预测除了给广告排序外,还会用于确定最终的扣费价格,如果ctr的概率预测的不准,会导致广告主的扣费偏高或偏低。
那么,为什么深度学习模型经常出现预测概率和真实情况差异大的问题?又该如何进行校准呢?这篇文章首先给大家介绍模型输出预测概率不可信的原因,再为大家通过10篇顶会论文介绍经典的校准方法,可以适用于非常广泛的场景。
1 为什么会出现校准差的问题
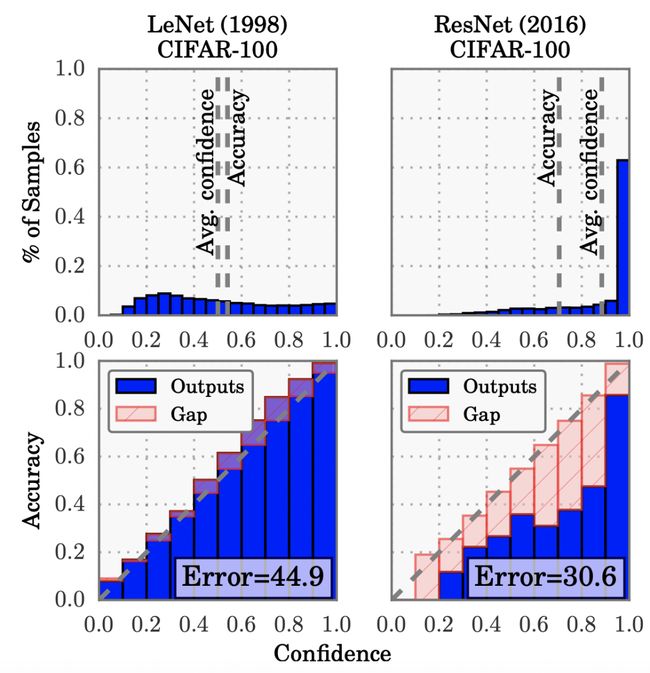
最早进行系统性的分析深度学习输出概率偏差问题的是2017年在ICML发表的一篇文章On calibration of modern neural networks(ICML 2017)。文中发现,相比早期的简单神经网络模型,现在的模型越来越大,效果越来越好,但同时模型的校准性越来越差。文中对比了简单模型LeNet和现代模型ResNet的校准情况,LeNet的输出结果校准性很好,而ResNet则出现了比较严重的过自信问题(over-confidence),即模型输出的置信度很高,但实际的准确率并没有那么高。
造成这个现象的最本质原因,是模型对分类问题通常使用的交叉熵损失过拟合。并且模型越复杂,拟合能力越强,越容易过拟合交叉熵损失,带来校准效果变差。这也解释了为什么随着深度学习模型的发展,校准问题越来越凸显出来。
那么为什么过拟合交叉熵损失,就会导致校准问题呢?因为根据交叉熵损失的公式可以看出,即使模型已经在正确类别上的输出概率值最大(也就是分类已经正确了),继续增大对应的概率值仍然能使交叉熵进一步减小。因此模型会倾向于over-confident,即对于样本尽可能的让模型预测为正确的label对应的概率接近1。模型过拟合交叉熵,带来了分类准确率的提升,但是牺牲的是模型输出概率的可信度。
如何解决校准性差的问题,让模型输出可信的概率值呢?业内的主要方法包括后处理和在模型中联合优化校准损失两个方向,下面给大家分别进行介绍。
2 后处理校准方法
后处理校准方法指的是,先正常训练模型得到初始的预测结果,再对这些预测概率值进行后处理,让校准后的预测概率更符合真实情况。典型的方法包括Histogram binning(2001)、Isotonic regression(2002)和Platt scaling(1999)。
Histogram binning是一种比较简单的校准方法,根据初始预测结果进行排序后分桶,每个桶内求解一个校准后的结果,落入这个桶内的预测结果,都会被校准成这个值。每个桶校准值的求解方法是利用一个验证集进行拟合,求解桶内平均误差最小的值,其实也就是落入该桶内正样本的比例。
Isotonic regression是Histogram binning一种扩展,通过学习一个单调增函数,输入初始预测结果,输出校准后的预测结果,利用这个单调增函数最小化预测值和label之间的误差。保序回归就是在不改变预测结果的排序(即不影响模型的排序能力),通过修改每个元素的值让整体的误差最小,进而实现模型纠偏。
Platt scaling则直接使用一个逻辑回归模型学习基础预测值到校准预测值的函数,利用这个函数实现预测结果校准。在获得基础预估结果后,以此作为输入,训练一个逻辑回归模型,拟合校准后的结果,也是在一个单独的验证集上进行训练。这个方法的问题在于对校准前的预测值和真实值之间的关系做了比较强分布假设。
3 在模型中进行校准
除了后处理的校准方法外,一些在模型训练过程中实现校准的方法获得越来越多的关注。在模型中进行校准避免了后处理的两阶段方式,主要包括在损失函数中引入校准项、label smoothing以及数据增强三种方式。
基于损失函数的校准方法最基础的是On calibration of modern neural networks(ICML 2017)这篇文章提出的temperature scaling方法。Temperature scaling的实现方式很简单,把模型最后一层输出的logits(softmax的输入)除以一个常数项。这里的temperature起到了对logits缩放的作用,让输出的概率分布熵更大(温度系数越大越接近均匀分布)。同时,这样又不会改变原来预测类别概率值的相对排序,因此理论上不会对模型准确率产生负面影响。
在Trainable calibration measures for neural networks from kernel mean embeddings(2018)这篇文章中,作者直接定义了一个可导的校准loss,作为一个辅助loss在模型中和交叉熵loss联合学习。本文定义的MMCE原理来自评估模型校准度的指标,即模型输出类别概率值与模型正确预测该类别样本占比的差异。
在Calibrating deep neural networks using focal loss(NIPS 2020)中,作者提出直接使用focal loss替代交叉熵损失,就可以起到校准作用。Focal loss是表示学习中的常用函数,对focal loss不了解的同学可以参考之前的文章:表示学习中的7大损失函数梳理。作者对focal loss进行推倒,可以拆解为如下两项,分别是预测分布与真实分布的KL散度,以及预测分布的熵。KL散度和一般的交叉熵作用相同,而第二项在约束模型输出的预测概率值熵尽可能大,其实和temperature scaling的原理类似,都是缓解模型在某个类别上打分太高而带来的过自信问题:
除了修改损失函数实现校准的方法外,label smoothing也是一种常用的校准方法,最早在Regularizing neural networks by penalizing confident output distributions(ICLR 2017)中提出了label smoothing在模型校准上的应用,后来又在When does label smoothing help? (NIPS 2019)进行了更加深入的探讨。Label smoothing通过如下公式对原始的label进行平滑操作,其原理也是增大输出概率分布的熵:
此外,一些研究也研究了数据增强手段对模型校准的影响。On mixup training: Improved calibration and predictive uncertainty for deep neural networks(NIPS 2019)提出mixup方法可以有效提升模型校准程度。Mixup是一种简单有效的数据增强策略,具体实现上,随机从数据集中抽取两个样本,将它们的特征和label分别进行加权融合,得到一个新的样本用于训练:
文中作者提出,上面融合过程中对label的融合对取得校准效果好的预测结果是非常重要的,这和上面提到的label smoothing思路比较接近,让label不再是0或1的超低熵分布,来缓解模型过自信问题。
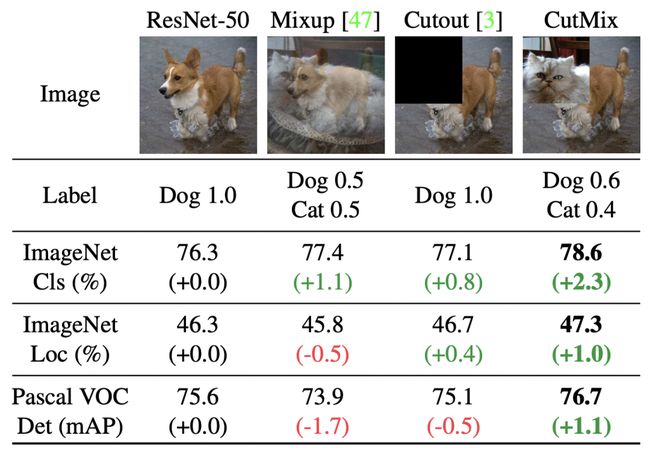
类似的方法还包括CutMix: Regularization Strategy to Train Strong Classifiers with Localizable Features(ICCV 2019)提出的一种对Mixup方法的扩展,随机选择两个图像和label后,对每个patch随机选择是否使用另一个图像相应的patch进行替换,也起到了和Mixup类似的效果。文中也对比了Mixup和CutMix的效果,Mixup由于每个位置都进行插值,容易造成区域信息的混淆,而CutMix直接进行替换,不同区域的差异更加明确。