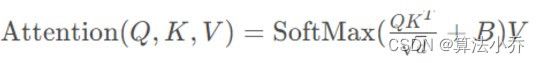Swin Transformer之相对位置编码详解
目录
一、概要
二、具体解析
1. 相对位置索引计算第一步
2. 相对位置索引计算第二步
3. 相对位置索引计算第三步
一、概要
在Swin Transformer采用了相对位置编码的概念。
那么相对位置编码的作用是什么呢?
解释:在解释相对位置编码之前,我们需要先了解一下在NLP中Position Encoder即PE,NLP中Position_Encoder理解
在Swin Transformer中,将特征图 如按7*7 的窗口大小划分为多个小窗格,单独在每个小窗格内进行Attention计算。这样一来,窗口内就相当于有 49个Token即49个像素值,这些像素是有一定的位置关系的,故在Attention计算时,需要考虑这些像素的位置关系,故提出了相对位置编码,其与NLP 中的PE是有异曲同工之妙的。
而不同的是NLP中是在QK.T之前加入了Position信息,而Swin Transformer是在QK.T之后加入的相对位置信息,但是在效果上都是一样的。
维度解析:
如果特征图的大小为2*2*N(N表示每个像素点的channels),那么经过拉直之后Q、K、V的维度都为4*N,那么QK.T 的维度就是4*4,其中第一个4表示4个像素点,第二个4表示对于每个像素点,相对包括自己在内的四个像素点的重要程度;而相对位置编码要得到的结果也需要是4*4,其每行表示四个像素相对于某个固定像素的位置编码值。
那么我们求出的相对位置编码就是对应的编码值吗?
答案是否定的,求出的相对位置编码只是对应的位置索引,其索引值取值范围为 0 ~ K,而这个索引其实对应的是一个长度为K的可学习向量。
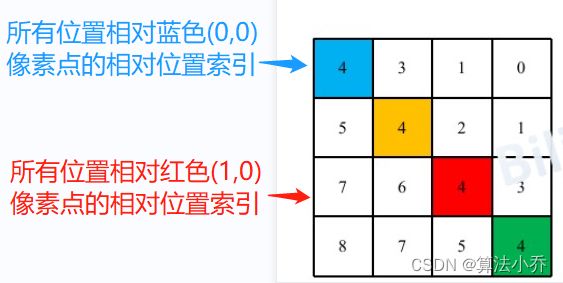
这个可学习向量会在训练过程中逐步更新,而相对位置索引,就是提供索引值,从这个可学习向量中得到最终的位置编码值。如下图所示:
而接下来我们要做的就是,用尽可能形象的方式,解释明白这个相对位置索引矩阵是怎么获取的,计算公式为:
其中的B就是根据相对位置索引矩阵(上图左侧)中的每个像素位置的索引,从可学习向量中获取的值,并组成的编码矩阵(上图右侧)。
二、具体解析
假设输入的feature map高宽都为2,那么首先我们可以构建出每个像素的绝对位置(左下方的矩阵),对于每个像素的绝对位置是使用行号y和列号x表示的。
1. 相对位置索引计算第一步
比如蓝色的像素对应的是第0行第0列所以绝对位置索引是( 0 , 0 ),蓝色像素使用q与所有像素k进行匹配过程中,是以蓝色像素为参考点。而相对位置偏置Bias就是相对每个像素情况下,不同QK的偏移值。
那么其他像素相对于该蓝色像素的相对位置是多少呢?
用蓝色像素的绝对位置索引与其他位置索引进行相减,就得到其他位置相对蓝色像素的相对位置索引,如下图所示
黄色(0,1)位置:(0,0) - (0,1) = (0,-1)
红色(1,0)位置:(0,0) - (1,0) = (-1,0)
绿色(1,1)位置:(0,0) - (1,1) = (-1,-1)
蓝色(0,0)位置相对于自己那就是(0,0)-(0,0)= (0,0)
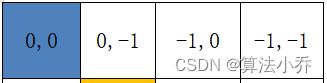
如下图所示,每个位置都是相对于蓝色(0,0)位置的相对值,其实就是差值。
将其拉直后就为:
同理,当其他位置作为相对位置时,计算方式是一样的,都是让当前元素与其他四个位置的坐标位置相减。结果分别为:
将它们拉直后,分别为:
那么将上面拉直后的结果,放在一起的话,如下图所示:
那么用代码是怎么计算的呢,是每个位置单独计算后,再拼接在一起的吗?
答案是否定的,往往在矩阵相关的计算中,都会以矩阵的方式进行统一计算。代码如下:
先整体来看,后面回分步解析。
# 获取特征图所有像素点的位置坐标
coords_h = torch.arange(2)
coords_w = torch.arange(2)
coords = torch.meshgrid([coords_h, coords_w])
# 横纵坐标合并后并拉直
coords = torch.stack(coords)
coords_flatten = torch.flatten(coords, 1)
# 计算坐标的相对位置差值
relative_coords_first = coords_flatten[:, :, None]
relative_coords_second = coords_flatten[:, None, :]
relative_coords = relative_coords_first - relative_coords_second
relative_coords = relative_coords.permute(1, 2, 0).contiguous() 分步解析:
(1)获取所有像素点的横坐标与纵坐标
a. 获取纵坐标的取值范围
coords_h = torch.arange(2)
coords_w = torch.arange(2)
'''
coords_h:
[0,1]
coords_w:
[0,1]
'''b.获取所有位置的纵坐标与横坐标
coords = torch.meshgrid([coords_h, coords_w])
'''
coords[0]:
[[0,0]
[1,1]]
shape与特征图大小相同2x2,每个位置的值表示该像素点
的纵坐标,第一行纵坐标均为0,第二行纵坐标均为1
coords[0]:
[[0,1
[0,1]]
shape与特征图大小相同2x2,每个位置的值表示该像素点
的横坐标,第一列横坐标均为0,第二列横坐标均为1
'''c. 上面的coords是一个列表,里面包括两个矩阵,即横坐标矩阵与纵坐标矩阵
将横坐标矩阵与纵坐标矩阵拼接起来,torch.stack,增加一个dim=0维度并拼接
coords = torch.stack(coords)
'''
coords:
shape:(2,2,2),第一个2表示横纵两种坐标,后面的2表示两行两列
'''
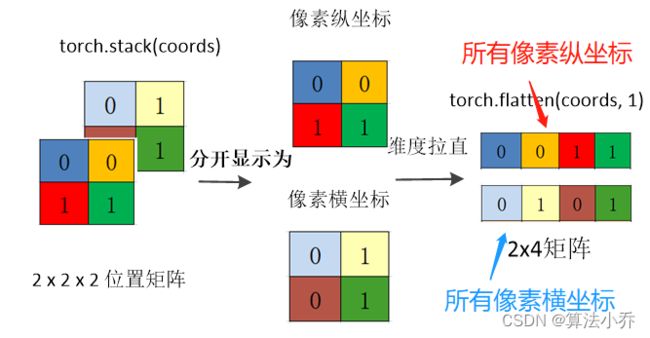
coords_flatten = torch.flatten(coords, 1)
'''
横坐标与纵坐标分别拉直
torch.flatten(coords,1)表示从第1个维度起拉直,
shape(2,2,2) -> (2,4)
'''d. 一共四个像素点,让每个像素点都其他包括自己在内的四个像素点的横纵坐标求差值。
所以就需要以行为单位(纵坐标与横坐标)每行各赋值4次,相当于每个像素的横纵坐标都复制4次,用于与四个像素点进行计算。
relative_coords_first = coords_flatten[:, :, None]
'''
增加一个维度,用于在以列为单位复制4次
shape(2,4,1)
'''横坐标与纵坐标都分别复制了4份。
复制后的,每行表示每个像素的横或纵坐标复制了4次。
relative_coords_first = coords_flatten[:, None, :]
'''
增加一个维度,用于在以行为单位复制4次
shape:(2,1,4)
'''所有坐标都分别复制4次。
复制后,每行表示所有像素的横或纵坐标。
relative_coords_first = coords_flatten[:, :, None]
relative_coords_second = coords_flatten[:, None, :]
relative_coords = relative_coords_first - relative_coords_second
relative_coords = relative_coords.permute(1, 2, 0).contiguous()
'''
上面的相减采用了广播机制,其广播的流程与上述的复制过程是一致的
'''上面这种做法是为了什么?
是为了两个矩阵相减,得到的结果就相当于,四个像素点依次作为主像素点时,其他四个像素相对于该主像素点的相对位置。如下图所示:
2. 相对位置索引计算第二步
注意!!! 这里描述的一直是相对位置索引,并不是相对位置偏执参数。后面我们会根据相对位置索引去取对应的参数。
上面已经计算出来相对某一个像素,其他像素点与其的坐标差值,如下:
但是上面的结果是二维的,而最终获取的位置参数表对于每个Head来说是一维的,故需要将上面的这个结果转换为一维的形式。由于索引值的范围为[-M+1,M-1],原始的相对位置索引加上M-1,使得索引值大于等于0,变为[0,2M-2]。
为什么要将索引值变为大于等于0呢?
这个问题其实很简单,因为我们在最后从参数表中获取最终值的方式,是通过索引,而索引值是不小于0的。
代码如下:
relative_coords[:, :, 0] += 2 - 1
relative_coords[:, :, 1] += 2 - 1relative_coords[:, :, 1] += 2 - 1
3. 相对位置索引计算第三步
对与每行,即不同像素间,希望得到的索引位置是不同的,但是如果直接横纵坐标相加的话,往往会出现像素不同,索引相同的情况,如下所示:
所以最后将所有横坐标都乘上2M-1,最后再将横坐标和纵坐标求和,这样每行不同像素间得到的索引就具有独一性。
relative_coords[:, :, 0] *= 2 * 2 - 1最后将行标和列标进行相加,得到独一的一维的索引,这样即保证了相对位置关系,而且不会出现上述0 +1 = 1 + 0 的问题了,是不是很神奇。
relative_position_index = relative_coords.sum(-1)至此就计算出了相对位置的索引,其并不是公式中的位置偏置参数。
真正使用到的可训练参数使保存在相对位置偏置表 relative position bias table中的,这个表的size为9,因为上面矩阵中索引值为0到8 是9个数。
即N = (2M-1)* (2M-1) = (4-1) * (4-1) =9.其是可训练的,随着训练过程,其内部的数值是不断优化更新的。
self.relative_position_bias_table = nn.Parameter(
torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)) 如relative position bias table如下所示:
所以可以,操作相对位置索引的数值,依次从table中获取对应的参数
至此,最终的相对位置编码才计算完毕。总体流程如下图所示: