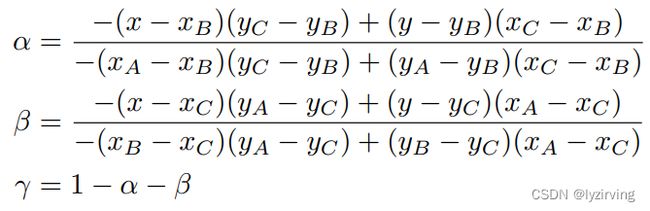【计算机图形学】光照模型和着色频率
最近在重温计算机图形学的基础知识，期望能做到温故知新，加深对其的理解，以便能从容应对工作中各种情况。
小弟水平有限，若有不正确之处，欢迎大家批评指正。
相关文章链接：
【计算机图形学基础】线性代数基础1
【计算机图形学基础】线性代数基础2
【计算机图形学基础】相机矩阵
【计算机图形学基础】投影矩阵
【计算机图形学基础】光照模型和着色频率
【计算机图形学基础】阴影映射
目录索引
- 1 Blinn-Phong光照模型
-
- 1.1 漫反射(diffuse reflection)
-
- 1.1.1 光的衰减
- 1.1.2 Lambert余弦定理
- 1.1.3 漫反射系数
- 1.1.4 漫反射公式
- 1.2 高光(specular highlights)
-
- 1.2.1 半程向量(bisector)
- 1.2.2 反光度(指数)压缩高光范围
- 1.3 环境光(ambient)
- 1.4 Blinn-Phong光照模型等式
- 2 着色频率
-
- 2.1 Flat shading
- 2.2 Gouraud shading
- 2.4 Phong shading
- 3 重心坐标
-
- 3.1 重心坐标表达式
- 3.2 特殊点：三角形重心
- 3.3 作用：利用重心坐标插值
- 4 参考
1 Blinn-Phong光照模型
Blinn-Phong光照模型 = 高光 + 漫反射 + 环境光，它是一个经验模型，各个组件的效果如上图所示。
光照模型是着色(shading)的一部分。着色时，每个点都是独立的一部分，有如下相关属性：
i ⃗ \vec{i} i：顶点到光源的方向向量；
n ⃗ \vec{n} n：顶点的法线向量；
v ⃗ \vec{v} v：顶点到相机的方向向量；
i ⃗ \vec{i} i、 n ⃗ \vec{n} n 和 v ⃗ \vec{v} v 都是单位向量。
1.1 漫反射(diffuse reflection)
特性：光线到达物体表面时，会被均匀的反射到各个方向，如下图所示。
在Blinn-Phong模型中，有三个要素影响漫反射：
一，有多少光线到达顶点；
二，有多少光线能被顶点接收；
三，该点会吸收多少漫反射光。
1.1.1 光的衰减
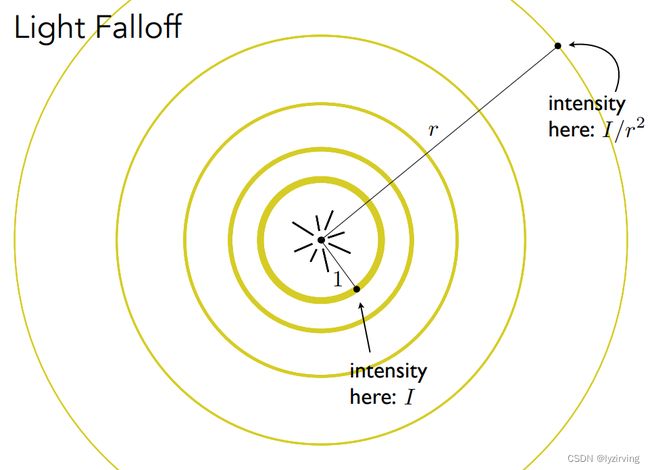
光源会发出光线。定义以单位距离为半径的光圈上，光的强度为 I I I。
由于能量守恒定律，在距离为 r r r 的光圈上，光线的强度为 I / r 2 I / r^{2} I/r2。
因此，上述等式定义了光线到达顶点后的光线强度，即有多少光到达顶点。
1.1.2 Lambert余弦定理
Lambert余弦定理表示顶点接收的光线总量和光线与顶点法线夹角的余弦成正比例，如图所示。
其中 c o s θ cos\theta cosθ = i ⃗ ∗ n ⃗ \vec{i} * \vec{n} i∗n。
若 θ = 0 \theta = 0 θ=0，则垂直入射，接受的光线最大；
若 θ = 90 \theta = 90 θ=90，此时该点接受不到任何光线。
综上，Lambert余弦定理表示有多少光能被该顶点接收。
1.1.3 漫反射系数
漫反射系数：表示该物质能吸收漫反射光的能力，一般用 k d kd kd 表示， k d kd kd 的值在[0, 1]。
当 k d = 1 kd = 1 kd=1 时，表示该点完全不吸收能量，入射的光线会被完全反射。
当 k d = 0 kd = 0 kd=0 时，表示该点会完全吸收光线，没有光线会被反射。
1.1.4 漫反射公式
在Blinn-Phong的反射模型中，漫反射光线由下式决定：
L d L_{d} Ld = k d k_{d} kd ∗ * ∗ ( I / r 2 I / r^{2} I/r2) ∗ * ∗ max ( 0 , i ⃗ ⋅ n ⃗ ) (0, \vec{i} \cdot \vec{n}) (0,i⋅n)。
上述公式中没有反射角，体现了漫反射的特性：光线达到物体表面后，会均匀的反射到各个方向。
Blinn-Phong中的漫反射是一个简化的经验模型，一定程度上体现了漫反射的效果。
1.2 高光(specular highlights)
特性：一，产生类似镜面反射的效果；二，观察方向和镜面反射方向接近的时候，能看到高光。
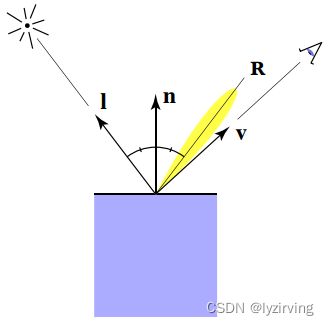
如图所示， i ⃗ \vec{i} i 是光源方向， n ⃗ \vec{n} n 是顶点法线向量， v ⃗ \vec{v} v 是观察向量， R ⃗ \vec{R} R 是光线镜面反射方向。
影响高光的因素有：
一，到达顶点的光线强度；
二，反射系数和反光度；
三，反射光线和观察方向的夹角。
其中第一点和第二点同漫反射类似。
针对第三点中，Blinn-Phong模型使用了半程向量来代替观察方向和镜面反射的夹角。
1.2.1 半程向量(bisector)
下图为正常反射的例子：
若视线和反射光想的夹角大于90度：
由于反射光分量因子一般取：max( c o s θ cos\theta cosθ, 0 0 0)，所以此时会造成反射光分量完全为0。
大多数情况下，这是可以接受的。但是若反光度很小的情况下，反射光高光的范围会变大，此时若反射光分量为0，就变得不可接受了。
因此，Blinn-Phong模型引入了半程向量来解决这个问题。
半程向量(bisector)实际是光线与视线夹角一半方向上的单位向量，如下所示：
Blinn-Phong模型用半程向量和顶点法线的夹角 α \alpha α 代替了镜面反射和观察方向的夹角。
不管观察方向在法线的左侧还是右侧，只要观察点在表面的上方，半程向量和法线的夹角都在[0, 90]度，规避了前述问题。
半程向量的计算方程如下：
h ⃗ \vec{h} h = v ⃗ + i ⃗ ∣ ∣ v ⃗ + i ⃗ ∣ ∣ \frac{\vec{v} + \vec{i}}{||\vec{v} + \vec{i}||} ∣∣v+i∣∣v+i；
因此，有： c o s ( α ) cos(\alpha) cos(α) = n ⃗ \vec{n} n ⋅ \cdot ⋅ h ⃗ \vec{h} h 。
使用半程向量另一好处就是简化了反射角的计算量。
1.2.2 反光度(指数)压缩高光范围
Blinn-Phong光照模型中，高光的计算式如下：
L s L_{s} Ls = k s k_{s} ks ( I / r 2 I / r^{2} I/r2) max ( 0 , n ⃗ ⋅ h ⃗ ) p (0, \vec{n} \cdot \vec{h})^{p} (0,n⋅h)p；
其中 k s k_{s} ks 是反射系数， I / r 2 I / r^{2} I/r2 是光线传播到顶点时的强度；
最后一项是 c o s ( α ) p cos(\alpha)^{p} cos(α)p，即半程向量和法向量夹角余弦的p次方。
指数p就是反光度，其作用为：缩小高光的范围，使其更真实。
如下图所示，对余弦的指数函数可以把余弦函数向左挤压，从而使高光的范围更小。
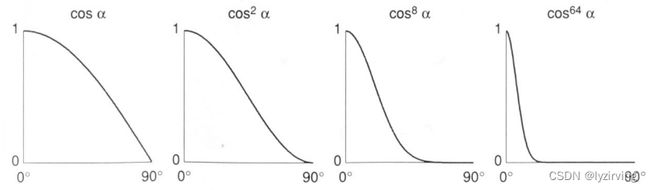
有如下例子：
同一行表示反射系数一致。同一行从左向右看去，反光度p在增大。反光度p增大的同时，高光范围在减小。
1.3 环境光(ambient)
特性：光线反射多次，从四面八方入射到顶点上。
例如杯子的一部分背对光源，但该部分不可能是完全黑色。因为四面八方的光线经过复杂传播后，会照射在该点上，这就是环境光的作用。
Blinn-Phong模型假设任何点接受到环境光的强度是相同的，记作 I a I_{a} Ia 。再加上环境光系数，就构成了环境光模型：
L a L_{a} La = k a k_{a} ka I a I_{a} Ia；
1.4 Blinn-Phong光照模型等式
L L L = L a L_{a} La + L s L_{s} Ls + L d L_{d} Ld；
L L L = k a k_{a} ka I a I_{a} Ia + k s k_{s} ks ( I / r 2 I / r^{2} I/r2) max ( 0 , n ⃗ ⋅ h ⃗ ) p (0, \vec{n} \cdot \vec{h})^{p} (0,n⋅h)p + k d k_{d} kd ∗ * ∗ ( I / r 2 I / r^{2} I/r2) ∗ * ∗ max ( 0 , i ⃗ ⋅ n ⃗ ) (0, \vec{i} \cdot \vec{n}) (0,i⋅n)；
综上，得到Blinn-Phong光照模型的计算等式，它是个经验模型。
2 着色频率
通过逐面着色、逐顶点着色和逐像素着色，可以将着色频率分为：flat shading、Gouraud shading和Phong shading。
2.1 Flat shading
flat shading：三角形面只有一个法向量，整个三角形只渲染一个颜色。
显而易见，flat shading对光滑物体是很不友好的，如下所示：
2.2 Gouraud shading
Grouraud shading是将着色应用在三角形每个顶点上，三角形每个顶点都有自己的法线。
三角形内部的点通过插值计算出其拥有的颜色值。
Grouraud shading效果如下所示：
通常用顶点四周三角面法线的简单平均值(或加权平均值)作为逐顶点法线，如下所示：
即 N v N_{v} Nv = Σ i N i ∣ ∣ Σ i N i ∣ ∣ \frac{\Sigma_{i}N_{i}}{||\Sigma_{i}N_{i}||} ∣∣ΣiNi∣∣ΣiNi
2.4 Phong shading
Phong shading是将着色应用在三角形内部每个像素上。
三角形三个顶点具有法线向量，然后进行插值，得到三角形内部各个像素的法向量，然后对每个像素进行着色。
Phong shading效果如下所示：
像素法向量的插值，可通过重心坐标求得。
3 重心坐标
重心坐标：三角形平面内任意点的坐标都可以表示为三角形三个顶点的线性组合。
重心坐标针对于某个特定的三角形。即 Δ A B C \Delta ABC ΔABC 定义一套重心坐标， Δ D E F \Delta DEF ΔDEF 又会定义另一套重心坐标。
点 ( x , y ) (x, y) (x,y) 的重心坐标表示为： ( x , y ) (x, y) (x,y) = α A \alpha A αA + β B \beta B βB + γ C \gamma C γC；
α \alpha α + β \beta β + γ \gamma γ = 1，系数满足此等式，表示点 ( x , y ) (x, y) (x,y)在 Δ A B C \Delta ABC ΔABC 的平面内。
若 α \alpha α >= 0 && β \beta β >= 0 && γ \gamma γ >= 0，表示点 ( x , y ) (x, y) (x,y) 在 Δ A B C \Delta ABC ΔABC 内部。
上述点A的重心坐标为 ( 1 , 0 , 0 ) (1, 0, 0) (1,0,0)。
3.1 重心坐标表达式
三角形任意点的重心坐标系数 = 对角 Δ \Delta Δ 面积 / Δ A B C \Delta ABC ΔABC面积。
因此，上述点重心坐标系数 α \alpha α = S Δ A a B C S Δ A B C \frac{S_{\Delta A_{a}BC}}{S_{\Delta ABC}} SΔABCSΔAaBC；
重心坐标系数 β \beta β = S Δ A b A C S Δ A B C \frac{S_{\Delta A_{b}AC}}{S_{\Delta ABC}} SΔABCSΔAbAC；
重心坐标系数 γ \gamma γ = S Δ A c A B S Δ A B C \frac{S_{\Delta A_{c}AB}}{S_{\Delta ABC}} SΔABCSΔAcAB；
当然，重心坐标也有一般的表达式：
3.2 特殊点：三角形重心
三角形的重心的重心坐标为( 1 3 \frac{1}{3} 31, 1 3 \frac{1}{3} 31, 1 3 \frac{1}{3} 31)。
因此三角形的重心把三角形分成等面积的三份。
3.3 作用：利用重心坐标插值
已知 Δ A B C \Delta ABC ΔABC 内部任意点 a a a 坐标为( x x x, y y y)，那么必然可以求得唯一的重心坐标( α \alpha α, β \beta β, γ \gamma γ)。
因此，可以利用( α \alpha α, β \beta β, γ \gamma γ)对该点上的任意属性进行插值(纹理坐标、颜色、法向量、深度等等)。
如 Δ A B C \Delta ABC ΔABC 的任意属性为 V V V，那么内部点 a a a 的属性 V V V 的值可插值为：
V a V_{a} Va = α \alpha α V A V_{A} VA + β \beta β V B V_{B} VB + γ \gamma γ V C V_{C} VC。
但是重心坐标有一个缺陷：在投影变换下，无法保证重心坐标不变。
因此要插值三维空间点的属性，需要在世界空间或相机空间中执行插值。
若投影后想要利用重心坐标进行插值，需要先进行逆变换。
4 参考
1 光照与基本着色模型
2 着色频率、图形管线、纹理映射