OpenCV-Python官方教程-16-直方图均匀化、2D直方图和直方图反向投影
- 直方图均衡化
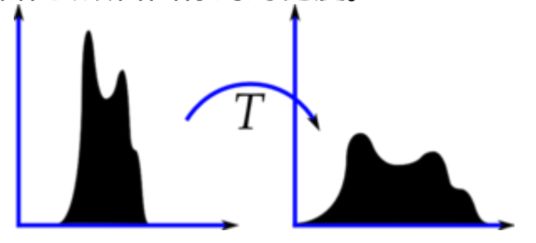
如果一幅图片整体很亮,那所有的像素值应该都会很高。但是一副高质量的图像的像素值分布应该很广泛。所以你应该把它的直方图做一个横向拉伸(如下图),这就是直方图均衡化要做的事情。通常情况下这种操作会改善图像的对比度。
1.1 先查原图的灰度直方图
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('apple.jpg',0)
flatten()将数组变成一维的
hist,bins = np.histogram(img.flatten(),256,[0,256])
#计算累积分布图
cdf = hist.cumsum()
cdf_normalized = cdf*hist.max()/cdf.max()
# plt.imshow(img,'gray')
plt.plot(cdf_normalized,color='b')
plt.hist(img.flatten(),256,[0,256],color='r')
plt.xlim([0,256])
plt.legend(('cdf','histogram'),loc='upper left')
plt.show()我们可以看出来直方图大部分在灰度值较高的部分,而且分布很集中。而我们希望直方图的分布比较分散,能够涵盖整个 x 轴。所以,我们就需要一个变换函数帮助我们把现在的直方图映射到一个广泛分布的直方图中。这就是直方图均衡化要做的事情。
1.2 使用Numpy进行灰度直方图均衡化
#构建Numpy掩膜数组,cdf为原数组,当数组元素为0时,掩盖(计算时被忽略)
cdf_m = np.ma.masked_equal(cdf,0)
cdf_m = (cdf_m - cdf_m.min())*255/(cdf_m.max()-cdf_m.min())
#对被掩盖的元素赋值,这里赋值为0
cdf = np.ma.filled(cdf_m,0).astype('uint8')
img2 = cdf[img]
hist,bins = np.histogram(img2.flatten(),256,[0,256])
#计算累积分布图
cdf = hist.cumsum()
cdf_normalized = cdf*hist.max()/cdf.max()
plt.plot(cdf_normalized,color='b')
plt.hist(img2.flatten(),256,[0,256],color='r')
plt.xlim([0,256])
plt.legend(('cdf','histogram'),loc='upper left')
plt.show()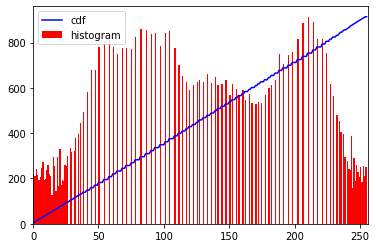
直方图均衡化经常用来使所有的图片具有相同的亮度条件的参考工具。这在很多情况下都很有用。例如,脸部识别,在训练分类器前,训练集的所有图片都要先进行直方图均衡化从而使它们达到相同的亮度条件。
1.3 Opencv直方图均衡化
img = cv2.imread('apple.jpg',0)
equ = cv2.equalizeHist(img)
res = np.hstack((img,equ))
# stacking images side-by-side
cv2.imshow('res',res)
cv2.waitKey(0)
cv2.destroyAllWindows()
1.4 CLAHE 有限对比适应性直方图均衡化
(1)背景:在上边做的直方图均衡化会改变整个图像的对比度,但是在很多情况下,这样做的效果并不好。例如,下图分别是输入图像和进行直方图均衡化之后的输出图像。

的确在进行完直方图均衡化之后,图片背景的对比度被改变了。但是你再对比一下两幅图像中雕像的面图,由于太亮我们丢失了很多信息。造成这种结果的根本原因在于这幅图像的直方图并不是集中在某一个区域。
为了解决这个问题,我们需要使用自适应的直方图均衡化。这种情况下,整幅图像会被分成很多小块,这些小块被称为“tiles”(在 OpenCV 中 tiles 的大小默认是 8x8),然后再对每一个小块分别进行直方图均衡化(跟前面类似)。所以在每一个的区域中,直方图会集中在某一个小的区域中(除非有噪声干扰)。如果有噪声的话,噪声会被放大。为了避免这种情况的出现要使用对比度限制。对于每个小块来说,如果直方图中的 bin 超过对比度的上限的话,就把其中的像素点均匀分散到其他 bins 中,然后在进行直方图均衡化。最后,为了去除每一个小块之间“人造的”(由于算法造成)边界,再使用双线性差值,对小块进行缝合。
下面的代码显示了如何使用 OpenCV 中的CLAHE。
#create a CLAHE object (Arguments are optional)
clahe = cv2.createCLAHE(clipLimit=2.0,tileGridSize=(8,8))
cl1 = clahe.apply(img)
cv2.imshow('clahe',cl1)
cv2.waitKey(0)
cv2.destroyAllWindows()- 2D直方图
在前面的部分我们介绍了如何绘制一维直方图,之所以称为一维,是因为我们只考虑了图像的一个特征:灰度值。但是在 2D 直方图中我们就要考虑两个图像特征。对于彩色图像的直方图通常情况下我们需要考虑每个的颜色(Hue)和饱和度(Saturation)。根据这两个特征绘制 2D 直方图。
使用函数 cv2.calcHist() 来计算直方图既简单又方便。如果要绘制颜色直方图的话,我们首先需要将图像的颜色空间从 BGR 转换到 HSV。
计算 2D 直方图,函数的参数要做如下修改:
(1)channels=[0,1] 因为我们需要同时处理 H 和 S 两个通道。
(2)bins=[180,256]H 通道为 180,S 通道为 256。
(3)
range=[0,180,0,256]H 的取值范围在 0 到 180,S 的取值范围在 0 到 256。
2.1 opencv的2D直方图
#opencv的2D直方图
import cv2
import numpy as np
img = cv2.imread('apple.jpg')
hsv = cv2.cvtColor(img,cv2.COLOR_BGR2HSV)
hist = cv2.calcHist([hsv],[0,1],None,[180,256],[0,180,0,256])
plt.imshow(hist,interpolation = 'nearest')
plt.show()# numpy 绘制2d直方图
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('apple.jpg')
hsv = cv2.cvtColor(img,cv2.COLOR_BGR2HSV)
hist,xbins,ybins = np.histogram2d(hsv[:,:,0].ravel(),hsv[:,:,1].ravel(),[180,256],[[0,180],[0,256]])
plt.imshow(hist,interpolation = 'nearest')
plt.show()- 直方图反向投影
直方图反向投影它可以用来做图像分割,或者在图像中找寻我们感兴趣的部分。简单来说,它会输出与输入图像(待搜索)同样大小的图像,其中的每一个像素值代表了输入图像上对应点属于目标对象的概率。用更简单的话来解释,输出图像中像素值越高(越白)的点就越可能代表我们要搜索的目标(在输入图像所在的位置)。这是一个直观的解释。直方图投影经常与camshift算法等一起使用。
首先我们要为一张包含我们要查找目标的图像创建直方图(在我们的示例中,我们要查找的是橘子,其他的都要)。
我们要查找的对象要尽量占满这张图像(换句话说,这张图像上最好是有且仅有我们要查找的对象)。最好使用颜色直方图,因为一个物体的颜色要比它的灰度能更好的被用来进行图像分割与对象识别。接着我们再把这个颜色直方图投
影到输入图像中寻找我们的目标,也就是找到输入图像中的每一个像素点的像素值在直方图中对应的概率,这样我们就得到一个概率图像,最后设置适当的阈值对概率图像进行二值化,就这么简单。
3.1 numpy方法
## 直方图反向投影
#numpy中的算法
import cv2
import numpy as np
from matplotlib import pyplot as plt
#roi是橘子的一部分
roi = cv2.imread('part_orange.jpg')
hsv = cv2.cvtColor(roi,cv2.COLOR_BGR2HSV)
target = cv2.imread('orange.jpg')
hsvt = cv2.cvtColor(target,cv2.COLOR_BGR2HSV)
M = cv2.calcHist([hsv],[0,1],None,[180,256],[0,180,0,256])
I = cv2.calcHist([hsv],[0,1],None,[180,256],[0,180,0,256])
R = M/I
h,s,v = cv2.split(hsvt)
B = R[h.ravel(),s.ravel()]
B = np.minimum(B,1)
B = B.reshape(hsvt.shape[:2])
disc = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(5,5))
B = cv2.filter2D(B,-1,disc)
B = np.uint8(B)
cv2.normalize(B,B,0,255,cv2.NORM_MINMAX)
ret,thresh = cv2.threshold(B,20,255,0)
cv2.imshow('ss',thresh)
cv2.waitKey(0)
cv2.destroyAllWindows()3.2 opencv的方法
##opencv中的反向投影
import cv2
import numpy as np
roi = cv2.imread('part_orange.jpg')
hsv = cv2.cvtColor(roi,cv2.COLOR_BGR2HSV)
target = cv2.imread('orange.jpg')
hsvt = cv2.cvtColor(target,cv2.COLOR_BGR2HSV)
roihist = cv2.calcHist([hsv],[0,1],None,[180,256],[0,180,0,256])
# 归一化:原始图像,结果图像,映射到结果图像中的最小值,最大值,归一化类型
# cv2.NORM_MINMAX 对数组的所有值进行转化,使他们线性映射到最小值和最大值之间
#归一化之后的直方图便于显示,归一化之后就成了0到255之间的数了
cv2.normalize(roihist,roihist,0,255,cv2.NORM_MINMAX)
dst = cv2.calcBackProject([hsvt],[0,1],roihist,[0,180,0,256],1)
# 此处卷积可以把分散的点连在一起
disc = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(5,5))
dst = cv2.filter2D(dst,-1,disc)
ret,thresh = cv2.threshold(dst,20,255,0)
thresh = cv2.merge((thresh,thresh,thresh))
res = cv2.bitwise_and(target,thresh)
res = np.hstack((target,thresh,res))
cv2.imshow('1',res)
cv2.waitKey(0)